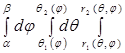Замена переменной в тройном интеграле

Пусть функция есть непрерывная на ограниченым области Е.

Пусть преобразование, , отображает область Е взаимно однозначно на область G в пространства с переменными u, v, w, причём обратное отображение области G на область Е осуществляеется преобразованием, ,. Функции, , — непрерывные вместе с частными производными, а якобиан на области G неравен нулю:

.

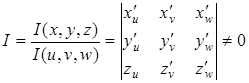
Рассуждая аналогично тому, как и при выводе формулы замены переменных в двойном интеграле, получаем формулу замены переменных в тройном интеграле:

=.

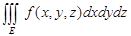
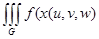
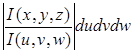
Замечание 1. Рассмотренное отображение называется регулярным. Можно доказать, что при регулярном отображении образом гладкой поверхности является гладкая поверхность; образом границы — граница; образом области является область, а также имеет место следующая теорема.

Теорема 1. Если функция f непрерывная на теле ЕOxyz и = — регулярное отображение тела Ouvw на тело Е, где тела Е и G — замкнутые кубируемые, то имеет место равенство (1) § 5, которое называют формулой замены переменных в тройном интеграле.

Тройка чисел однозначно характеризует положение точки в пространстве 0xyz и называется кривалинейными координатами этой точки. Поверхности в пространстве 0xyz, определяемые равенствами v=const, u=const, w=const, называются координатными поверхностями. Через каждую точку области Е проходит по одной поверхности из каждого семейства координатных поверхностей.

Рассмотрим два частных случая кривалинейных координат в пространстве R³, которые широко используются при вычислении тройных интегралов методом замены переменных.

Цилиндрические координаты Пусть точека М в прямоугольной декартовай системе координат 0xyz имеет координаты. Задавая проекцию точки М на плоскость при помощью полярных координат r, положение точки М можно определить с помощью трёх чисел, которые называт цилиндрическими координатами точки М. Если полярная ось совпадает с положительным направлением оси 0х, то формулы:

, z=r,, , (2).

задают связь между цилиндрическими и декартовыми координатами.

Координатной поверхностью в цилиндрической системе координат являются: цилиндрические поверхности r=const, полуплоскости =const, которая проходит через ось 0z, и плоскость z=const, параллельная х0у.

Пусть система координат отображается на систему координат 0xyz по формулам (2), т. е., тогда якобиан этогоотображения:

.

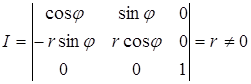
Замечание 2. Если область Е в пространстве 0xyz можно задать в цилиндрических координатах неравенствами, , то тройной интеграл сводится к повторному интегралу.

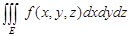
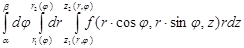
= (3).

Сферические координаты.

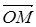
Пусть точка М (x, y, z) в прямоугольной системе координат 0xyz знаходится на расстоянии от начала координат О. Обозначим через угол между положительным направлением оси 0z и вектором. Пусть есть полярный угол проекции точки М на плоскость х0у. Тогда положение точки М можно задать с помощью трёх чисел, которые называют сферическими координатами точки М. Сферические координаты связаны с декартовыми следующими формулами:

.

(4).

Координатными поверхностями в сферических координатах являются: сфера, полуплоскость, которая проходит через ось 0z, и коническая поверхность с осью 0z.

Найдём якобиан преобразования (5):

.

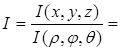
На основании равенства (1) § 3 выводим формулу замены переменных в сферических координатах:

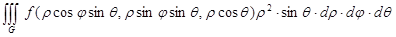
=. (5).

Замечание 3. Если область Е в пространстве 0xyz можно задать в сферических координатах неравенствами, то тройной интеграл (5) сводится к повторному интегралу.

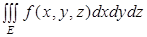
= (6).