Основы статистики. 
Основы статистики

1. Имеется информация по промышленным предприятиям города за отчетный год:

Табл. 1.

1. Произведем группировку промышленных предприятий по стоимости основных средств.

Первым шагом определим величину интервала группировочного признака по следующей формуле:

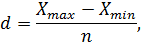
где:

• — максимальная стоимость основных средств,
• — минимальная стоимость основных средств,

— количество групп.

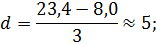
Посредством вышеуказанной формулы мы получили 3 группы:

I группа — от 8 до 13 млн руб.,.

II группа — от 14 до 19 млн руб.,.

III группа — от 20 до 25 млн руб.

Следующим шагом построим вспомогательную таблицу, в которой в каждой группе определим число предприятий, имеющих соответствующий объем продукции и полученную прибыль.

Табл. 2.

Опираясь на вышеуказанные данные можно сказать, что с увеличением стоимости основных средств средняя прибыль на одно предприятие увеличивается и, как следствие, увеличивается прибыль.

2. Имеются следующие данные о годовом росте объема отправок пассажиров на предприятии воздушного транспорта:

Табл. 3.

1. Определение показателей динамики изменения объема перевозок.

Вычислим абсолютный прирост по формуле:

Для вычисления темпа роста необходимо рассчитать коэффициент роста:

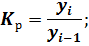
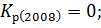
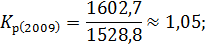
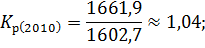
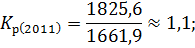
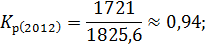
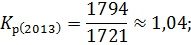
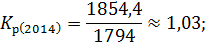
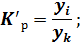
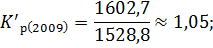
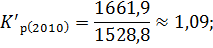
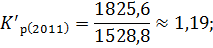
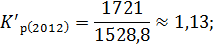
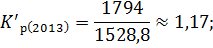
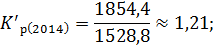
Зная коэффициенты роста вычислим темпы роста по следующей формуле:

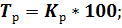
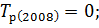
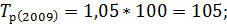
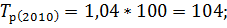
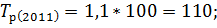
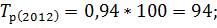
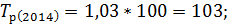
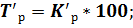
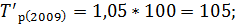
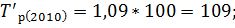
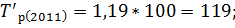
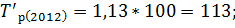
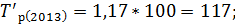
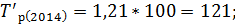
Следующим шагом вычислим темпы прироста по следующей формуле:

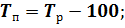
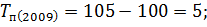
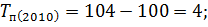
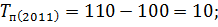
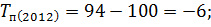
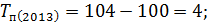
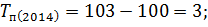
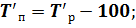
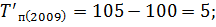
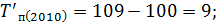
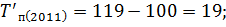
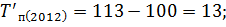
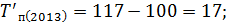
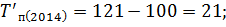
Вычислим цепные показатели (ускорение и абсолютное значение 1% прироста):

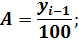
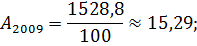
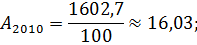
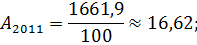
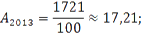
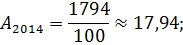
Средний уровень объема перевозок пассажиров на предприятии воздушного транспорта за весь анализируемый период:

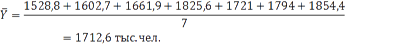
Теперь можно оформить все результаты вычислений в общую таблицу:

Табл. 4.

2. Расчет основной тенденции изменения объема перевозок.

Выявление общей тенденции развития перевозок целесообразно осуществлять методом аналитического выравнивания, то есть путем определения модели развития (тренда) без выявления факторов динамики.

Закономерность изменения представляется в виде функции времени:

где — выровненный уровень на момент времени t;

t — момент времени.

Вид уравнения (тренда) определяется характером динамики. Для определения формы тренда и расчета параметров тренда составим вспомогательную таблицу:

Табл. 5

В соответствии с данными вышеуказанной таблицы выравнивание следует проводить по линейной зависимости, так как наблюдаются более или менее стабильные абсолютные приросты (цепные).

Система нормальных уравнений имеет вид:

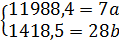
a=1712,6;

b=50,7.

Модель тренда имеет вид:

3. Расчет прогноза объема перевозок:

Точечный прогноз:

• · для 2015 года:
• · для 2016 года:

Интервальный прогноз при экстраполяции определяется формулой:

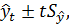
где — точечный прогноз, рассчитанный по модели;

t — коэффициент доверия по распределению Стьюдента при уровне значимости a.

— среднее квадратическое отклонение тренда.

Составим вспомогательную таблицу для дальнейших вычислений:

Табл. 6.

Определим среднее квадратическое отклонение тренда по следующей формуле:

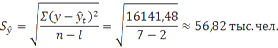
Коэффициент доверия t=2,4 (при вероятности P=0,95).

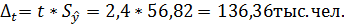
Интервальный прогноз:

· для 2015 года:

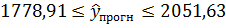
· для 2016 года:

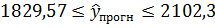
3. Данные по предприятию воздушного транспорта, обслуживающему линии в северном регионе, представлены в следующей таблице:

Табл. 7.

1. Для выявления наличия или отсутствия сезонной неравномерности строится линейная диаграмма:

Рис. 1

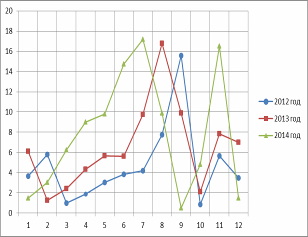
группировочный экстраполяция интервальный Линейная диаграмма показывает наличие сезонной неравномерности, так как, несмотря на увеличение отправок пассажиров от года к году, максимальный и минимальный объемы отправок за три года практически приходятся на одинаковые месяцы.

2. Уровни объема отправок имеют тенденцию к развитию (от года к году повышаются), поэтому индексы сезонности исчисляются по формуле:

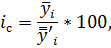
где — средняя суточная из фактических уровней одноименных месяцев;

— средняя суточная из сглаженных (выровненных) суточных уровней одноименных месяцев.

Рассчитаем среднесуточные из фактических уровней одноименных месяцев:

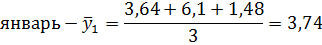
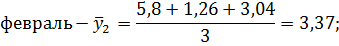
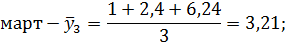
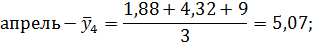
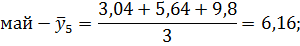
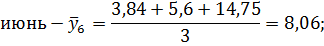
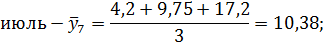
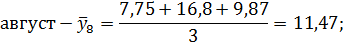
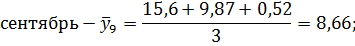
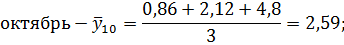
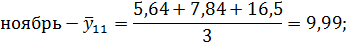
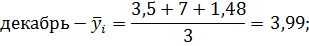
Для нахождения срединного периода, к которому может быть отнесена двенадцатимесячная скользящая средняя, выполняется центрирование, то есть определение средней из найденных скользящих средних. Центрированные скользящие средние рассчитываются следующим образом:

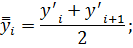
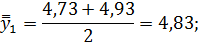
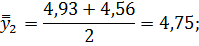
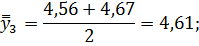
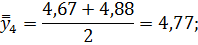
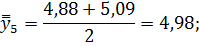
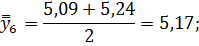
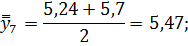
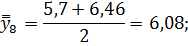
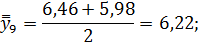
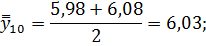
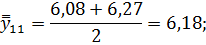
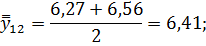
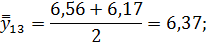
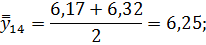
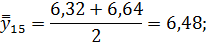
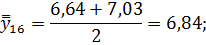
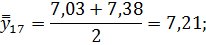
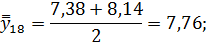
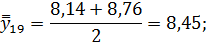
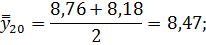
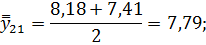
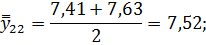
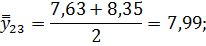
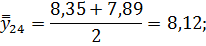
Определим средние из сглаженных (центрированных скользящих) среднесуточных уровней одноименных месяцев:

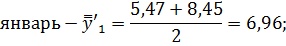
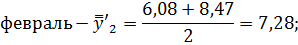
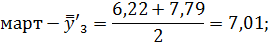
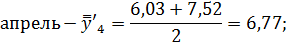
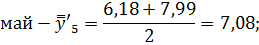
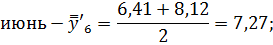
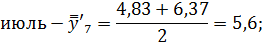
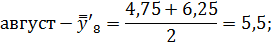
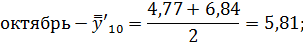
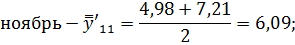
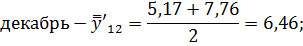
Последним шагом в данном вопросе найдем индексы сезонности по следующим формулам:

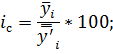
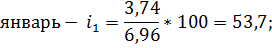
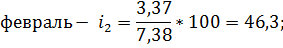
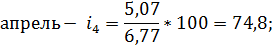
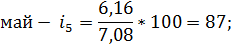
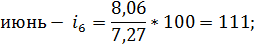
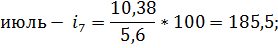
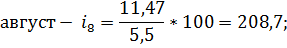
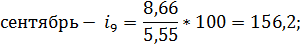
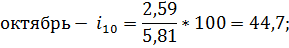
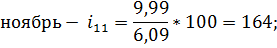
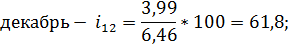
Теперь можно сгруппировать все результаты вычислений в общую таблицу:

Табл. 8

Распределение объема перевозок пассажиров на следующий год осуществляется следующим образом:

1. Определяем среднесуточный объем отправок по следующей формуле:

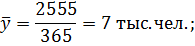
2. Определяем объем отправок пассажиров для каждого месяца:

Сумма расчетных значений по месяцам составляет 2644,4 тыс.чел. Расхождение между годовым объемом перевозок и суммой расчетных значений составляет 89,4 тыс.чел., или 3,5%, что объясняется допущенными округлениями при расчете индексов сезонности.