Теорема Вигнера. 
Спектроскопия кристаллов

Каждому уровню энергии соответствует неприводимое представление группы симметрии.

При действии преобразования симметрии на волновую функцию, удовлетворяющую уравнению Шредингера, должна получиться волновая функция, удовлетворяющая этому уравнению Шредингера.

• 2) Эти волновые функции, относящиеся к одному значению энергии, образуют представление группы.
• 3) Это представление, относящееся к одному значению энергии уровня, неприводимо по построению, т.к. эти преобразующиеся друг через друга волновые функции должны относиться к одному значению энергии.

Таким образом, каждому уровню энергии системы соответствует неприводимое представление, размерность его равна кратности вырождения уровня, которая определяет сколько волновых функций или нормальных координат соответствует данному уровню (двукратно вырожденной частоте соответствуют две волновые функции, две нормальных координаты).

Эти соображения дают возможность произвести классификацию собственных колебаний молекулы без того, чтобы решать сложную задачу о конкретном определении ее нормальных координат. Для этого надо найти представление, осуществляемое всеми колебательными координатами — полное представление. Это полное представление приводимо, и разлагая его на неприводимые части, мы определим кратность собственных частот и свойства симметрии соответствующих колебаний. Одно и тоже неприводимое представление может входить в приводимое несколько раз. Это означает, что имеется несколько различных частот одинаковой кратности и симметрии.

Для нахождения полного представления в качестве функций базиса возьмем не нормальные координаты, а компоненты ui векторов смещения ядер от их положений равновесия, так как характеры представления инвариантны относительно линейного преобразования функций базиса.

При вычислении характера элемента G группы надо рассмотреть только те ядра, положения равновесия которых остаются на месте при данном преобразовании симметрии.

Рассмотрим поворот С () на угол вокруг оси. Ux, uy, uz — компоненты вектора смещения некоторого ядра, положение равновесия которого находится на самой оси и поэтому не затрагивается поворотом.

Ux=ux cos+ uy cos (90 —).

Uy=-ux cos (90 —) + uy cos.

Uz= uz.

Характер — сумма диагональных элементов … матрицы.

1 + 2 cos. Если на оси Nc атомов, то суммарный характер Nc (1 + 2 cos). Это характер, соответствующий преобразованию 3N смещений. Выделим из него часть, соответствующую поступательному и вращательному движению как целого. Поступательное перемещение определяется вектором u центра инерции молекулы, соответствующая часть характера 1 + 2 cos. Поворот определяется.

вектором d — аксиальный вектор, по величине равный углу поворота и направленный вдоль оси поворота. По отношению к поворотам аксиальный вектор ведет себя как обычный вектор, поэтому соответствующий характер равен 1 + 2 cos.

• (С)= (Nc-2) (1 + 2 cos)
• — характер поворота в колебательном представлении. Для тождественного преобразования Е характер равен (Е)=3N — 6, Nc=N.

Для зеркального поворота.

ux = ux cos + uy sin.

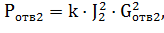
Uy = -ux sin + uy cos.

Uz= - uz.

Характер равен — 1 + 2cos. Характер зеркального поворота в полном представлении.

Ns (-1 + cos).

Вектору смещения центра инерции молекулы соответствует характер — 1 + 2cos. Аксиальный вектор d при отражении в плоскости h не меняется, а при отражении в плоскости v изменяется на обратный.

S ()=C () h = C (+) I, h= C () I, C () = 1 + 2cos,.

а при инверсии аксиальный вектор не меняется.

— 1 + 2cos + 1 — 2cos.

Характер зеркального поворота в колебательном представлении равен.

(S)= Ns (- 1 + 2cos). N,.

После определения характеров полного или механического представления остается разложить его на неприводимые части по формуле.

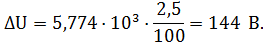
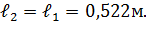
Пример. Произвести классификацию нормальных колебаний молекулы аммиака NH3. Точечная группа молекулы аммиака C3v. Выписываем характеры точечной группы из таблиц.

Число инвариантных атомов, т. е. атомов остающихся на месте при данном преобразовании симметрии, для тождественного преобразования Е — 4, для операции поворота на 120 градусов C3 -1 и для отражения в плоскости — 2. Характеры полного колебательного представления:

0)=6.

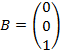
Разлагаем это приводимое представление на неприводимые части по формуле, где g — порядок группы или число элементов симметрии в группе, — характер приводимого представления, — характер неприводимого представления. Для аммиака g=6. Число, показывающее, сколько раз неприводимое представление А1 входит в приводимое представление nA1=1/6(6+6)=2. nA2=1/6(6−6)=0. nE=1/6(12)=2. То есть у молекулы аммиака должно быть 2 полносимметричных колебаний, преобразующихся по представлению А1, и две двукратновырожденных частоты, преобразующихся по представлении Е.