Решение нелинейных уравнений с одним неизвестным

интегрирование численный погрешность уравнение Общие сведения о численном решении уравнений с одним неизвестным.

Пусть задана непрерывная функция f (x). Требуется найти корни уравнения f (x) = 0 численными методами — это и является постановкой задачи. Численное решение уравнения распадается на несколько подзадач:

Анализ количества, характера и расположения корней (обычно путем построения графика функции или исходя из физического смысла исследуемой модели). Здесь возможны следующие варианты:

единственный корень;

бесконечное множество решений;

корней нет;

имеется несколько решений, как действительных, так и мнимых (например, для полинома степени n). Корни четной кратности выявить сложно.

Локализация корней (разбиение на интервалы) и выбор начального приближения к каждому корню. В простейшем случае можно протабулировать функцию с заданным шагом.

Если в двух соседних узлах функция будет иметь разные знаки, то между этими узлами лежит нечетное число корней уравнения (по меньшей мере один).

Вычисление каждого (или интересующего нас) корня уравнения с требуемой точностью. Уточнение происходит с помощью методов, изложенных ниже.

Метод дихотомии (бисекций).

Иначе называется методом половинного деления. Пусть задан начальный интервал [x0, x1], на котором f (x0)f (x1)? 0 (т.е. внутри имеется не менее чем один корень). Найдем x2 = Ѕ (x0 + x1) и вычислим f (x2). Если f (x0)f (x2)? 0, используем для дальнейшего деления отрезок [x0, x2], если > 0 — используем для дальнейшего деления отрезок [x1, x2], и продолжаем деление пополам.

Итерации продолжаются, пока длина отрезка не станет меньше 2о — заданной точности. Тогда середина последнего отрезка даст значение корня с требуемой точностью. В качестве иного критерия можно взять | f (x)|? оy.

Скорость сходимости метода невелика, однако он прост и надежен. Метод неприменим к корням четной кратности. Если на отрезке несколько корней, то заранее неизвестно, к какому из них сойдется процесс.

Если на заданном интервале предполагается несколько корней, то существует возможность последовательно исключать найденные корни из рассмотрения. Для этого воспользуемся вспомогательной функцией, где — только что найденный корень. Для функций f (x) и g (x) совпадают все корни, за исключением (в этой точке полюс функции g (x)). Для достижения требуемой точности рекомендуется грубо приблизиться к корню по функции g (x), а затем уточнить его, используя f (x).

Метод хорд Идея метода проиллюстрирована рисунком. Задается интервал [x0, x1], на котором f (x0)f (x1)? 0, между точками x0 и x1 строится хорда, стягивающая f (x). Очередное приближение берется в точке x2, где хорда пересекает ось абсцисс. В качестве нового интервала для продолжения итерационного процесса выбирается тот, на концах которого функция имеет разные знаки. Условия выхода из итерационного цикла: или.

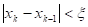
| f (x)|? оy.

Для вывода итерационной формулы процесса найдем точку пересечения хорды (описываемой уравнением прямой) с осью абсцисс:

ax2 + b = 0,.

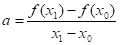
где; b = f (x0) — ax0.

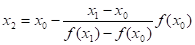
Отсюда легко выразить .

Метод хорд в большинстве случаев работает быстрее, чем метод дихотомии. Недостатки метода те же, что и в предыдущем случае.

Метод Ньютона (касательных) Пусть x0 — начальное приближение к корню, а f (x) имеет непрерывную производную. Следующее приближение к корню найдем в точке x1, где касательная к функции f (x), проведенная из точки (x0, f0), пересекает ось абсцисс. Затем точно так же обрабатываем точку (x1, f1), организуя итерационный процесс. Выход из итерационного процесса по условию .

Уравнение касательной, проведенной из точки (x0, f0): y (x) = f /(x0)(x-x0) + f (x0) дает для y (x1) = 0 следующее выражение:

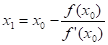
(1).

которое и используется для организации итерационного процесса. Итерации сходятся, только если всюду выполняется условие; в противном случае сходимость будет не при любом начальном приближении, а только в некоторой окрестности корня. Итерации будут сходиться к корню с той стороны, с которой .

Метод обладает самой высокой скоростью сходимости: погрешность очередного приближения примерно равна квадрату погрешности предыдущего приближения. Метод можно использовать для уточнения корней в области комплексных чисел, что необходимо при решении многих прикладных задач, например при численном моделировании электромагнитных колебательных и волновых процессов с учетом временной и пространственной диссипации энергии.

Недостатком метода можно указать необходимость знать явный вид первой и второй производных, так как их численный расчет приведет к уменьшению скорости сходимости метода. Иногда, ради упрощения расчетов, используют т.н. модифицированный метод Ньютона, в котором значение f /(x) вычисляется только в точке x0, при этом число итераций увеличивается, но расчеты на каждой итерации упрощаются.

Метод секущих В отличие от метода Ньютона, можно заменить производную первой разделенной разностью, найденной по двум последним итерациям, т. е. заменить касательную секущей. При этом первый шаг итерационного процесса запишется так:

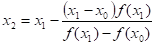
Для начала итерационного процесса необходимо задать x0 и x1, которые не обязательно ограничивают интервал, на котором функция должна менять знак; это могут быть любые две точки на кривой. Выход из итерационного процесса по условию .

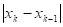
Сходимость может быть немонотонной даже вблизи корня. При этом вблизи корня может происходить потеря точности, т.н. «разболтка решения», особенно значительная в случае кратных корней. От разболтки страхуются приемом Гарвика: выбирают некоторое оx и ведут итерации до выполнения условия. Затем продолжают расчет, пока убывает. Первое же возрастание может свидетельствовать о начале разболтки, а значит, расчет следует прекратить, а последнюю итерацию не использовать.

Метод простых итераций Суть метода простых итераций в принципе совпадает с методом, изложенным для решения систем линейных алгебраических уравнений. Для нелинейного уравнения метод основан на переходе от уравнения.

f (x) = 0 (2).

к эквивалентному уравнению x = ц (x). Этот переход можно осуществить разными способами, в зависимости от вида f (x). Например, можно положить:

ц (x) = x + bf (x), (3).

где b = const, при этом корни исходного уравнения (2) не изменятся.

Если известно начальное приближение к корню x0, то новое приближение x1 = ц (x0), т. е. общая схема итерационного процесса:

xk+1 = ц (xk). (4).

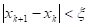
Наиболее простой критерий окончания процесса .

Критерий сходимости метода простых итераций: если вблизи корня |ц/(x)| < 1, то итерации сходятся. Если указанное условие справедливо для любого x, то итерации сходятся при любом начальном приближении. Исследуем выбор константы b в функции (3) с точки зрения обеспечения максимальной скорости сходимости. В соответствии с критерием сходимости наибольшая скорость сходимости обеспечивается при |ц/(x)| = 0. При этом, исходя из (3),.

b = -1/f /(x), и итерационная формула (4) переходит в.

.

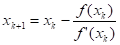
т.е. в формулу метода Ньютона (1). Таким образом, метод Ньютона является частным случаем метода простых итераций, обеспечивающим самую высокую скорость сходимости из всех возможных вариантов выбора функции ц (x).