Нелинейное программирование. 
Методы оптимизации. 
Алгоритмы. 
Линейное программирование

5.1 Задача условной оптимизации с ограничениями-равенствами (задача Лагранжа)

Рассмотрим задачу минимизации целевой функции, в которой все ограничения заданы в виде равенств.

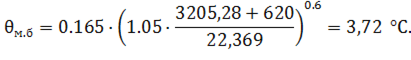
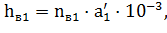
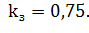
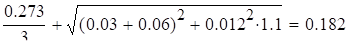
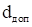
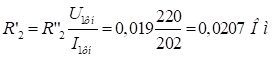
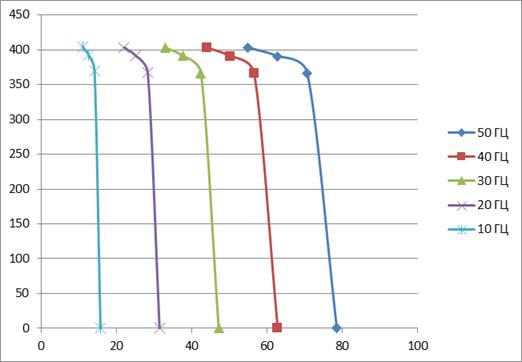
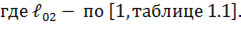
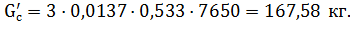
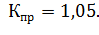
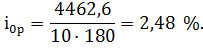
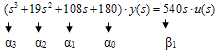
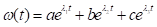
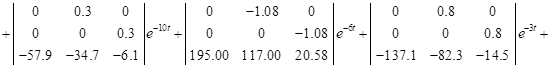
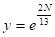
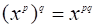
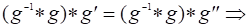
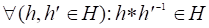
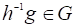
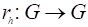
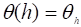
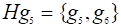
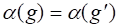
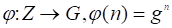
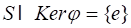
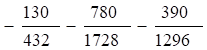
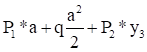
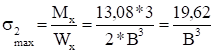
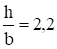
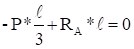
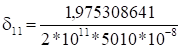
Построим функцию, которую назовем функцией Лагранжа,.

(5.2).

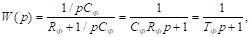
переменные, называют множителями Лагранжа.

Если функции, непрерывно дифференцируемы, то верна следующая теорема.

Эта теорема позволяет, решив систему уравнений.

найти точки, и затем среди полученных точек отобрать оптимальные решения задачи (5.1). Но при этом используются достаточные условия оптимальности. Получим их. Сравним значения целевой функции в точках и, где — вектор приращений. Тогда, если и — допустимые решения, то.

.

и .

Разложим функцию в ряд Тейлора, получим.

=.

В точке выполняются необходимые условия из теоремы и, следовательно,. Итак,, где вектор приращений удовлетворяет условиям. Если функции разложить в ряд Тейлора до слагаемых первого порядка малости, то условия, накладываемые на приращения, приобретут вид. Полученный результат сформулируем в виде теоремы.

Алгоритм решения задачи Лагранжа.

• 1. Преобразуйте задачу к виду (5.1), когда правые части ограничений нули.
• 2. Постройте функцию Лагранжа.
• 3. Найдите все стационарные точки функции Лагранжа.
• 4. Каждую стационарную точку проверьте на оптимальность, используя достаточные условия оптимальности.
• 5.2 Задачи условной оптимизации с ограничениями-неравенствами

Рассмотрим задачу, в которой ограничения являются нестрогими неравенствами.

Функция Лагранжа для этой задачи:, где переменные , — множители Лагранжа.

Определение 5.1. Точка, где, называется седловой точкой функции Лагранжа, если в этой точке выполняются неравенства для всех .

Доказательство. Для седловой точки выполняется неравенство, или для любого.

. (5.4).

Перепишем неравенство (5.4) для точки, определив ее координаты по формуле. Получим, а так как k выбирали произвольно, то этот результат верен для любого k. Это означает, что .

Теперь перепишем неравенство (5.4) для точки, определив ее координаты по формуле. Получим для произвольного k. С другой стороны по определению седловой точки, и, что было доказано выше. Следовательно, для всех k, то есть .

Следующая теорема устанавливает связь между седловой точкой функции Лагранжа и оптимальным решением.

Первая теорема Куна-Таккера. Если седловая точка функции Лагранжа, то оптимальное решение задачи (5.3).

Доказательство. По определению седловой точки, и. Учитывая вид функции Лагранжа и лемму, получаем для, а значит тем более для. При этом. Тогда,, и. А это означает, что — оптимальное решение задачи (5.3).

Контр-пример к первой теореме Куна-Таккера Приведем пример задачи, функция Лагранжа которой не имеет седловой точки:

Функция Лагранжа для этой задачи имеет вид. У данной задачи единственное допустимое решение, которое является оптимальным решением Покажем, что при точка не является седловой, то есть не выполняется для всех неравенство.

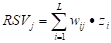
. (5.5).

Действительно, если, то из неравенства (5.5) получаем, что верно не для всех. Если и, то (5.5) преобразуется к виду, и вновь приходим к выводу, что неравенство (5.5) выполняется не для всех .

5.3 Выпуклое программирование

Определение 5.2. Задачей выпуклого программирования называется задача минимизации выпуклой функции на выпуклом множестве, или преобразуемая в таковую эквивалентными преобразованиями.

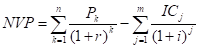
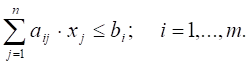
Очевидно, что задача (5.3) является задачей выпуклого программирования при условии, что все входящие в нее функции — выпуклые. Если все ограничения задачи (5.1) линейные, а целевая функция выпуклая, то эта задача то же будет задачей выпуклого программирования.

Определение 5.3. Ограничение задачи (5.3) называется регулярным, если существует допустимое решение задачи, при котором .

Определение 5.4. Если все ограничения задачи регулярные, то говорят о регулярности самой задачи.

Условия седловой точки для гладких функций (условия Куна-Таккера).

Теоремы Куна-Таккера дают метод нахождения оптимального решения задачи (5.3) через поиск седловых точек функции Лагранжа. Поэтому особый интерес вызывают условия, определяющие седловые точки. Получим эти условия для непрерывно дифференцируемых функций.

Предположим, что все функции в задаче (5.3) выпуклые и непрерывно дифференцируемые. Тогда можно сформулировать необходимые и достаточные условия седловой точки функции Лагранжа, называемые условиями Куна-Таккера.

Теорема 5.2. Точка является седловой точкой функции Лагранжа задачи выпуклого программирования тогда и только тогда, когда в ней выполняются условия Куна-Таккера:

, (5.6).

.

Доказательство.

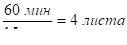
Точка седловая и в ней по переменной x достигается минимум в области и максимум по переменной y в области. Следовательно, если, то частная производная в точке либо равна 0, либо положительна. Если, то частная производная в точке равна 0. Это можно записать, используя условие дополняющей нежесткости.

для .

В векторной форме этот результат выглядит так.

.

Аналогично выводится группа условий для переменной y.

В условиях Куна-Таккера, а функция, являясь неотрицательной линейной комбинацией выпуклых функций, — выпуклая функция. Из теоремы об эквивалентных условиях выпуклости из выпуклости функции следует.

.

Используя равенство, и неравенство, получаем для всех. И так, доказано неравенство для всех .

Вспомним вид функции Лагранжа:

.

Из условий Куна-Таккера.

.

Следовательно,.

для всех .

Или для всех. Доказано, что точка — седловая.

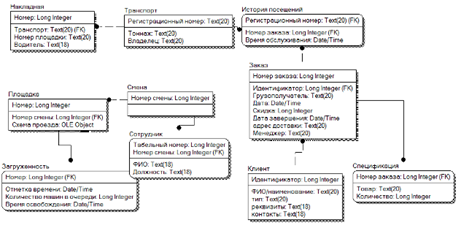
В таблице 5.1 приведены условия Куна-Таккера для общей задачи выпуклого программирования:

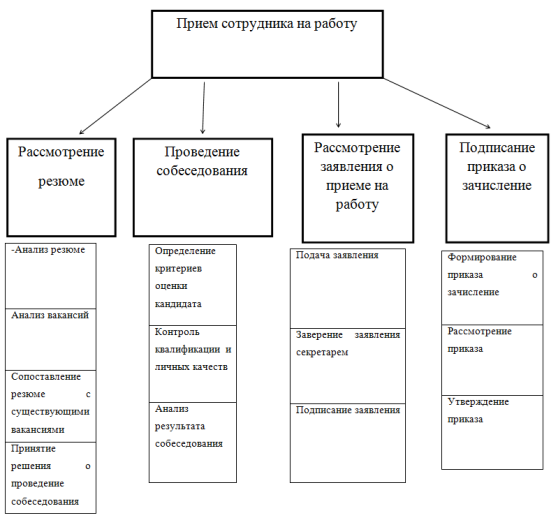
где.

Таблица 5.1 — Условия Куна-Таккера к задаче (5.7).

Ограничение задачи.	Соответствующие ограничению условия Куна-Таккера в точке.
	,.
,.

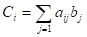
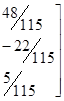
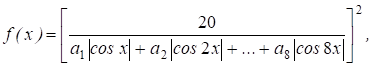
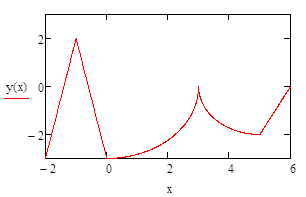
Если исходная задача является задачей выпуклого программирования, функции в задаче непрерывно дифференцируемы, а ограничения регулярные, то можно любую данную точку проверить на оптимальность.

Алгоритм проверки точки на оптимальность.

• 1. Преобразовать задачу к виду (5.7), выписав все функции .
• 2. Проверить выпуклость всех функций, входящих в ограничения-неравенства, и линейность, входящих в ограничения-равенства. Доказать регулярность каждого из нелинейных ограничений.
• 3. Выписать условия Куна-Таккера, подставив в них координаты точки .
• 4. Если полученная система имеет решение, то — седловая точка функции Лагранжа, а — оптимальное решение задачи (5.7) по 1-й теореме Куна-Таккера. В противном случае по второй теореме Куна-Таккера не является оптимальным решением. Проверка завершается.