Применение статистики в решении экономических проблем

Задача 1.

Условие: Имеется информация о количестве книг, полученных студентами по абонементу за прошедший учебный год.

Построить вариационный, ранжированный, дискретный ряд распределения, обозначив элементы ряда.

Решение: Ранжированным называется ряд, в котором значения признака расположены либо в порядке убывания, либо в порядке возрастания. Дискретным вариационным рядом распределения называется ранжированная совокупность вариантов с соответствующими им частотами .

Выпишем все различные значения величин в порядке возрастания и подсчитаем их частоты. Полученный дискретный вариационный ранжированный ряд представлен в Таблице1.

Таблица 1 — Дискретный вариационный ранжированный ряд

Задача 2.

Условие: В таблице приведены данные о продажах автомобилей в одном из автосалонов города за 1 квартал прошедшего года. Определите структуру продаж.

Решение: Чтобы определить структуру продаж надо рассчитать относительные величины структуры. ОВС это показатель, характеризующий долю отдельных частей изучаемой совокупности во всем ее объеме.

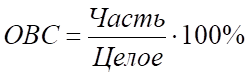
Автомобили Skoda:

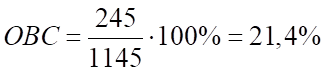
Автомобили Hyundai:

Автомобили Daewoo:

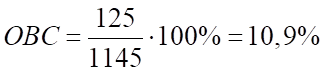
Автомобили Nissan:

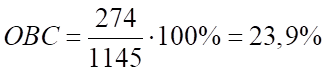
Автомобили Renault:

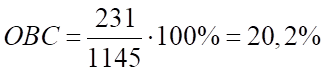
Автомобили Kia:

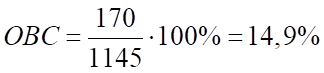
Результаты расчетов представлены в Таблице 2.

Таблица 2 — Структура продаж автомобилей в автосалоне

Лидером продаж являются автомобили Nissan. Удельный вес их продаж составляет 23,9%. Наименьшую долю продаж 8,7% составляют продажи автомобилей Hyundai.

Задача 3.

Условие: Имеется информация о численности студентов ВУЗов города и удельном весе (%) обучающихся студентов на коммерческой основе:

Определить:

• 1) средний удельный вес студентов ВУЗов, обучающихся на коммерческой основе;
• 2) число этих студентов.

Решение: 1) Средний удельный вес студентов ВУЗов, обучающихся на коммерческой основе определяется по формуле:

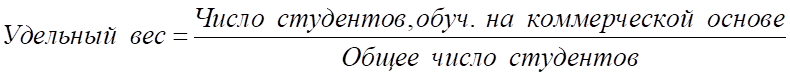
Числитель неизвестен, применим формулу средней арифметической взвешенной:

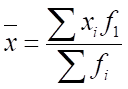
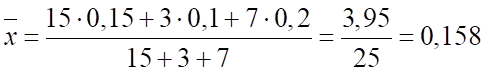
или 15,8%.

Средний удельный вес студентов ВУЗов, обучающихся на коммерческой основе, составляет 15,8%.

2) Найдем число студентов, обучающихся на коммерческой основе: тыс. чел.

Задача 4.

Условие: При изучении влияния рекламы на размер среднемесячного вклада в банках района обследовано 2 банка. Получены следующие результаты:

Определить:

для каждого банка: а) средний размер вклада за месяц; б) дисперсию вклада;

средний размер вклада за месяц для двух банков вместе.

Дисперсию вклада для 2-х банков, зависящую от рекламы;

Дисперсию вклада для 2-х банков, зависящую от всех факторов, кроме рекламы;

Общую дисперсию используя правило сложения;

Коэффициент детерминации;

Корреляционное отношение.

Решение: Для расчета числовых характеристик заменим интервальный ряд дискретным. Все значения признака в пределах интервала приравниваем к его срединному значению, и считаем, что частота относится к середине интервала. Открытый интервал «До 500» заменяем закрытым интервалом «480 — 500», величина которого равна величине ближайшего к нему интервала, то есть 20.

Таблица 3 — Расчетная таблица

Размер месячного вклада, рубли.	Середина интервала,.	Банк с рекламой.	Банк без рекламы.
Число вкладчиков,.	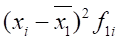Число вкладчиков,.
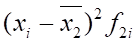480−500.							8363,52.
500−520.							4303,36.
520−540.							2785,28.
540−560.							777,6.
560−580.							4439,04.
580−600.							11 139,2.
600−620.
620−640.
Итого.	;

1) а) Средний размер вклада за месяц банк с рекламой: руб.

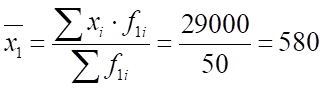
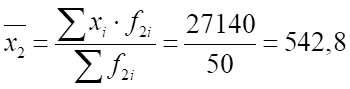
банк без рекламы: руб.

б) Дисперсия вклада банк с рекламой:

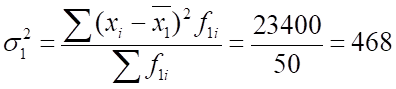
банк без рекламы:

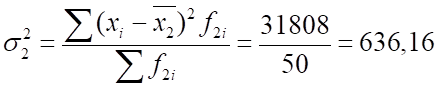
2) Средний размер вклада за месяц для двух банков вместе найдем как среднюю взвешенную из групповых средних:

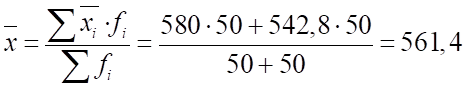
руб.

3) Дисперсия вклада для 2-х банков, зависящая от рекламы:

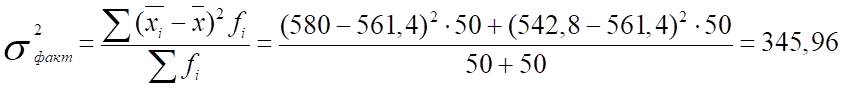
4) Дисперсия вклада для 2-х банков, зависящая от всех факторов, кроме рекламы:

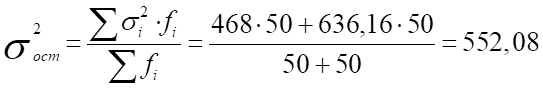
5) Общая дисперсия, используя правило сложения:

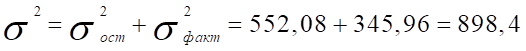
6) Коэффициент детерминации:

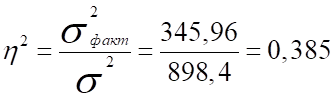
Таким образом, размер месячного вклада на 38,5% зависит от наличия рекламы и на 61,5% от других факторов.

7) Корреляционное отношение:

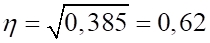
Итак, между рекламой и размером месячного вклада существует заметная связь.

Задача 5.

Условие: Имеется информация о выпуске продукции (работ, услуг), полученной на основе 10% выборочного наблюдения по предприятиям области:

Определить:

• 1) по предприятиям, включенным в выборку:
  • а) средний размер произведенной продукции на одно предприятие;
  • б) дисперсию объема производства;
  • в) долю предприятий с объемом производства продукции более 400 тыс. руб.;
• 2) в целом по области с вероятностью 0,954 пределы, в которых можно ожидать:
  • а) средний объем производства продукции на одно предприятие;
  • б) долю предприятий с объемом производства продукции более 400 тыс. руб.;
• 3) общий объем выпуска продукции по области.

Решение: Рассчитаем середины интервалов и заменим интервальный ряд дискретным. Открытые интервалы «До 100» и «500 и >» заменяем закрытыми. Середины этих интервалов определяем, исходя из предположения, что величина открытого интервала равна величине ближайшего к нему интервала, то есть для нашей задачи равна100.

Таблица 4 — Расчетная таблица

Группы предприятий по объему продукции, тыс. руб.	Середина интервала,.	Число предприятий,.
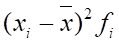0 — 100.
100 — 200.
200 — 300.
300 — 400.
400 — 500.
500 — 600.
Итого:

1) а) средний размер произведенной продукции на одно предприятие:

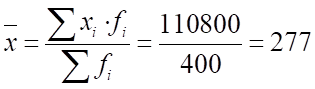
тыс.руб.

б) дисперсия объема производства:

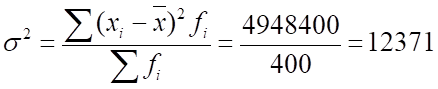
в) доля предприятий с объемом производства продукции более 400 тыс. руб.:

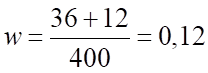
или 12%.

• 2) в целом по области с вероятностью 0,954 пределы, в которых можно ожидать:
  • а) средний объем производства продукции на одно предприятие.

Найдем число предприятий области:

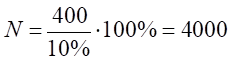
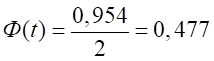
По таблице значений интегральной функции Лапласа находим значение аргумента, такое, что, получаем .

Средний объем производства продукции на одно предприятие в целом по области отличается от выборочного среднего объема на величину ошибки выборки :

.

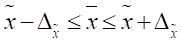
Предельную ошибку выборки находим по формуле:

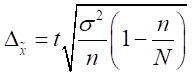
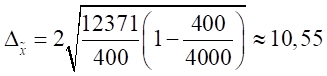
тыс.руб.

С вероятностью 0,954 можно утверждать, что средний объем производства продукции на одно предприятие по области находится в пределах от 266,45 тыс. руб. до 287,55 тыс. руб.

б) долю предприятий с объемом производства продукции более 400 тыс. руб.:

Предельная ошибка для доли:

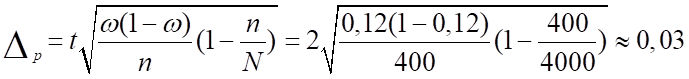
Доверительный интервал для генеральной доли:

С вероятностью 0,954 можно утверждать, что доля предприятий с объемом производства продукции более 400 тыс. руб. по области составит от 9% до 15%.

3) Общий объем выпуска продукции по области составит в среднем:

млн. руб.

Общий объем выпуска продукции по области составит от млн. руб. до млн. руб.

Задача 6.

Условие: Данные о площадях под картофелем до и после изменения границ района, тысяч гектаров:

Сомкнуть ряд, выразив площадь под картофелем в условиях изменения границ района.

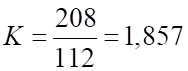
Решение: Определим коэффициент пересчета уровней в 3 периоде, когда произошло изменение границ района: .

Умножая на этот коэффициент уровни ряда динамики в прежних границах, приводим их к сопоставимым уровням в новых границах.

Другой способ смыкания рядов динамики рядов заключается в том, что уровни периода, в котором произошли изменения (в нашей задаче 3 периода), как до изменений, так и после изменений (для нашей задачи 112 и 208) принимаются за 100%, а остальные — пересчитываются в процентах по отношению к этим уровням соответственно (до изменений — по отношению к 112; а после изменений — по отношению к 208).

В результате получается сомкнутый ряд (Таблица 5).

Таблица 5. — Динамика площадей под картофелем

Задача 7.

Условие: По нижеприведенным данным ответить на вопросы, поставленные в таблице, т. е. определить недостающие показатели.

Решение: Используем взаимосвязь индексов. Индивидуальный индекс товарооборота:

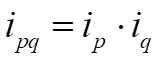
Для II квартала:

;

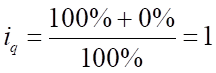
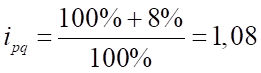
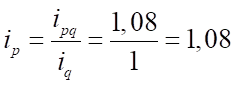
Тогда .

То есть цена увеличилась во II квартале на 8% по сравнению с предыдущим.

Для III квартала:

;

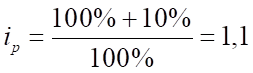
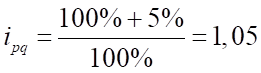
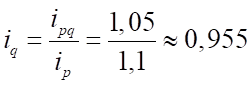
Тогда .

То есть натуральный объем продаж уменьшился в III квартале на 4,5% по сравнению с предыдущим.

Для IV квартала:

; ;

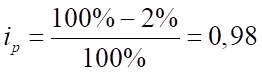
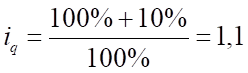
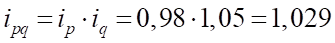
Тогда .

То есть товарооборот в денежном выражении увеличился в IV квартале на 2,9% по сравнению с предыдущим.

Результаты решения представлены в таблице 6.

Таблица 6 — Результаты расчетов

Задача 8.

Условие: По пяти рабочим цеха имеются данные о квалификации и месячной выработке. Для изучения связи между квалификацией рабочих и их выработкой определить линейное уравнение связи и коэффициент корреляции. Дать интерпретацию коэффициентам регрессии и корреляции.

Решение: Составим расчетную таблицу 7.

Таблица 7 — Расчетная таблица

Уравнение линейной парной регрессии имеет вид.

.

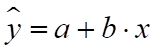
Найдем коэффициенты теоретического уравнения регрессии методом наименьших квадратов:

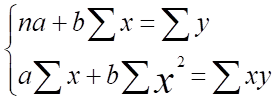
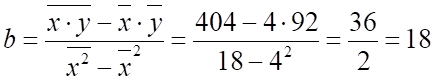
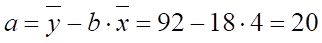
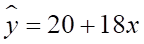
Получили уравнение: .

Т.е. с увеличением разряда на единицу выработка продукции за смену увеличится на 18 штук.

Рассчитаем дисперсии и среднеквадратические отклонения:

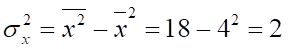
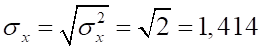
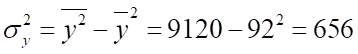
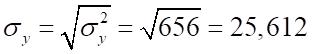
Рассчитаем линейный коэффициент корреляции :

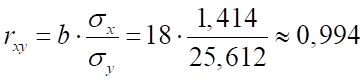
Коэффициент корреляции близок к единице и положителен, значит, между квалификацией рабочих и их выработкой наблюдается прямая очень тесная линейная связь.

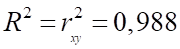
Коэффициент детерминации показывает, что уравнением регрессии объясняется 98,8% дисперсии результативного признака (т.е. выработки продукции за смену), а на долю прочих факторов приходится лишь 1,2%.

Задача 9.

Условие: Имеются следующие данные за 2006 год:

численность населения, тыс чел.: на 1 января — 430,0;

на 1 апреля — 430,2;

на 1 июля 430,3;

на 1 октября — 430,7;

на 1 января 2007 г. 430,8.

. число умерших, чел. — 8 170.

. число выбывших на постоянно жительство в другие населенные пункты, чел. — 570.

. коэффициент жизненности — 1,075.

. доля женщин в общей численности населения, % - 58.

. доля женщин в возрасте 15−49 лет в общей численности женщин, % - 39.

Определите: коэффициенты рождаемости, смертности, естественного, механического и общего прироста населения; число родившихся; число прибывших на постоянно жительство из других населенных пунктов; специальный коэффициент рождаемости.

Решение: Найдем среднюю численность населения за 2006 год. Так как интервалы между наблюдениями расположены через равные промежутки времени, то используем формулу простой хронологической средней:

тыс. чел.

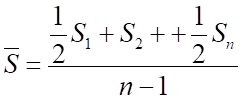
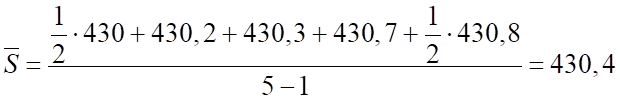
Рассчитаем число родившихся, зная коэффициент жизненности:

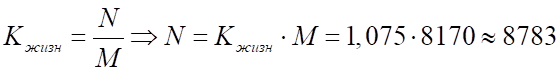
чел.

Коэффициент рождаемости:

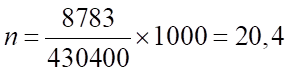
Т.е. рождаемость в расчете на каждую 1000 чел. населения составляла в 2006 году приблизительно 20 — 21 чел.

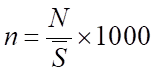
Для характеристики рождаемости используется специальный коэффициент рождаемости (показатель фертильности) или плодовитости женщин в возрасте 15−49 лет:

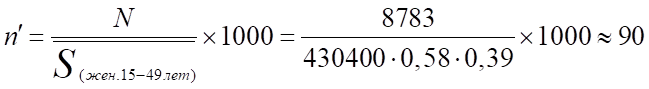
Т. е. в среднем на 1000 женщин в возрасте от 15 до 49 лет приходится 90 рождений.

Коэффициент смертности:

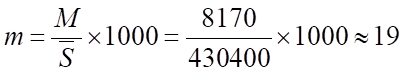
Т.е. смертность в расчете на каждую 1000 чел. населения составляла в 2006 году приблизительно 19 чел.

Коэффициент естественного прироста населения:

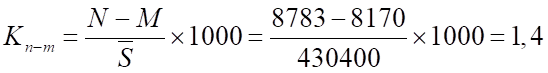
Естественный прирост населения в течение 2006 года в среднем на 1000 человек составлял от 1 до 2 человек.

Найдем число прибывших на постоянное жительство из других населенных пунктов.

чел.

На постоянное жительство из других населенных пунктов в 2006 году прибыло 757 человек.

Коэффициент механического прироста населения:

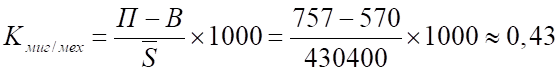
Механический (миграционный) прирост населения в течение 2006 года в среднем на 1000 человек составлял от 0 до 1 человека.

Коэффициент общего прироста населения:

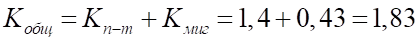
Общий прирост населения в течение 2006 года в среднем на 1000 человек составлял от 1 до 2 человек.

Задача 10.

Условие: Имеются данные на конец года по РФ, млн. чел.:

• — численность населения — 146,7
• — экономически активное население — 66,7
• — безработных, всего — 8,9, в том числе

зарегистрированных в службе занятости — 1,93.

Определить:

• 1) уровень экономически активного населения;
• 2) уровень занятости;
• 3) уровень безработицы;
• 4) уровень зарегистрированных безработных;
• 5) коэффициент нагрузки на 1 занятого в экономике.

Решение: 1) Уровень экономически активного населения:

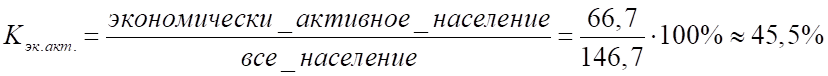
2) Экономически активное население включает в себя занятых и безработных поэтому, число занятых: 66,7 — 8,9 = 57,8 млн. чел.

Уровень занятости:

3) Уровень безработицы:

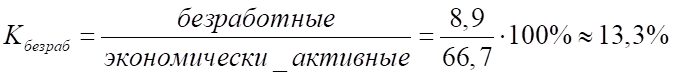
4) Уровень зарегистрированных безработных:

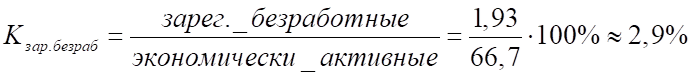
5) Коэффициент нагрузки на одного занятого в экономике — это число не занятых в экономике, приходящееся на одного занятого:

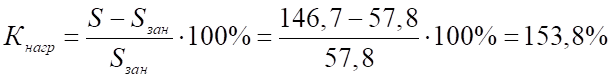
дисперсия вариационный ранжированный.

• 1) Гусаров В. М. Статистика: Учебное пособие для ВУЗов. М.: ЮНИТИ-ДАНА, 2002.
• 2) Елисеева И. И., Юзбашев М. М. Общая теория статистики. М.: ФиС, 2004.
• 3) Ефимова М. Р., Рябцев В. М. Общая теория статистики. М.: ФиС, 2003.
• 4) Салин В. Н., Шпаковская Е. П. Социально-экономическая статистика. — М.: Юристъ, 2000.
• 5) Социально-экономическая статистика. Практикум/под ред. В. Н. Салина, Е. П. Шпаковской. М.: ФиС, 2003.
• 6) Шмойлова Р. А., Минашкин В. Г., Садовникова Н. А. Практикум по теории статистики. М.: ФиС, 2006.