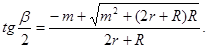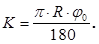Разбивка серпантины. 
Камеральное трассирование автомобильной дороги IV категории

При трассировании дороги по крутому склону часто приходится разбивать линию в виде зигзагов с очень острыми внутренними углами. В этом случае нет возможности сопрягать прямые участки при помощи обычных закруглений, т.к. вследствие большой разности высот между НК и КК и незначительной длины самого закругления получаются большие продольные уклоны, намного превышающие предельные. В связи с этим сопряжение линий на таких участках осуществляется при помощи сложных внешних закруглений, называемых серпантинами. На косогорных трассах серпантины часто проектируют также для обхода оврагов, ущелий и других препятствий.

Основными элементами серпантины являются (рис.2):

• 1. Основная круговая кривая FDE радиуса R;
• 2. Две вспомогательные кривые AP и BG c радиусами r₁ и r₂;
• 3. Две прямые вставки или переходные кривые PF = m₁ и EG = m₂.

Если радиусы вспомогательных кривых и прямые вставки серпантина соответственно равны, т. е. r₁ = r₂ и m₁ = m₂, то она называется симметричной.

Серпантины разрешают устраивать на дорогах III-IV категорий.

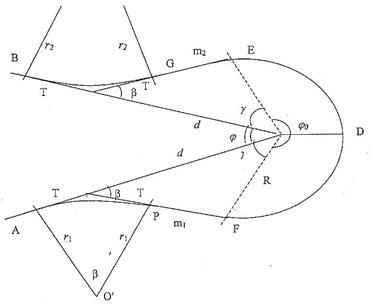
Рис. 2. Разбивка симметричной серпантины

Расчет симметричной серпантины При расчете серпантина обычно задаются радиусом основной кривой R, радиусами вспомогательных кривых r, а также величинами прямых вставок.

Основные элементы (в, d, г, ц₀), необходимые для разбивки серпантина на местности, вычисляют.

Угол поворота вспомогательной кривой в находится по формуле:

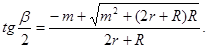
(12).

Расстояние от вершины вспомогательной кривой до центра основной кривой, равно:

Угол в центре серпантины, определяющий направление на начальную или конечную точки основной кривой, равен:

(14).

а центральный угол основной кривой.

(15).

Длина основной кривой.

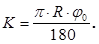
(16).

Пример разбивки симметричного серпантина:

R = 70 м, r = 150 м, m₁=m₂=30 м.

tg = 0,3614 > в = 39°44'23?,.

Т = r * tg = 54,21 м,.

d = 109,49 м, г = 90° - в = 48°,.

ц = 111°16?36?,.

К_вк= 109,9 м, К= 186,49 м.

В ПП устанавливаем теодолит, ориентируемся на вершину предыдущего угла поворота, откладываем величину d и получаем т. М. Из полученной точки откладываем величину Т и получаем т. А — начало серпантина. Из т. М ориентируем прибор на т. О и откладываем угол в. Вдоль полученного направления откладываем величину Т, получаем т. Р — конец вспомогательной кривой. Из т. О ориентируемся на т. М и откладываем угол г, вдоль полученного направления откладываем величину R — получаем т. F — начало основной кривой. Вторую часть серпантина разбивают аналогично.

Основная кривая разбивается и закрепляется на местности колышками через 3−5 м.