Решение задач линейного программирования

Решение задачи линейного программирования симплекс методом

Симплекс-метод является основным в линейном программировании. Решение задачи начинается с рассмотрений одной из вершин многогранника условий. Если исследуемая вершина не соответствует максимуму (минимуму), то переходят к соседней, увеличивая значение функции цели при решении задачи на максимум и уменьшая при решении задачи на минимум. Таким образом, переход от одной вершины к другой улучшает значение функции цели. Так как число вершин многогранника ограничено, то за конечное число шагов гарантируется нахождение оптимального значения или установление того факта, что задача неразрешима.

Этот метод является универсальным, применимым к любой задаче линейного программирования в канонической форме. Система ограничений здесь — система линейных уравнений, в которой количество неизвестных больше количества уравнений. Если ранг системы равен r, то мы можем выбрать r неизвестных, которые выразим через остальные неизвестные. Не всегда можно выражать через остальные первые r неизвестных. Однако такие r неизвестных обязательно найдутся. Эти неизвестные (переменные) называются базисными, остальные свободными. Придавая определенные значения свободным переменным и вычисляя значения базисных (выраженных через свободные), мы будем получать различные решения нашей системы ограничений. Таким образом, можно получить любое ее решение. Нас будут интересовать особые решения, получаемые в случае, когда свободные переменные равны нулю. Такие решения называются базисными, их столько же, сколько различных базисных видов у данной системы ограничений. Базисное решение называется допустимым базисным решением или опорным решением, если в нем значения переменных неотрицательны. Если в качестве базисных взяты переменные X₁, X₂, …, X_r, то решение {b₁, b₂,…, b_r, 0, …, 0} будет опорным при условии, что b₁, b₂,…, b_r? 0.

Симплекс-метод основан на теореме, которая называется фундаментальной теоремой симплекс-метода. Среди оптимальных планов задачи линейного программирования в канонической форме обязательно есть опорное решение ее системы ограничений. Если оптимальный план задачи единственен, то он совпадает с некоторым опорным решением. Различных опорных решений системы ограничений конечное число. Поэтому решение задачи в канонической форме можно было бы искать перебором опорных решений и выбором среди них того, для которого значение F самое большое. Но, во-первых, все опорные решения неизвестны и их нужно находить, a, во-вторых, в реальных задачах этих решений очень много и прямой перебор вряд ли возможен. Симплекс-метод представляет собой некоторую процедуру направленного перебора опорных решений. Исходя из некоторого, найденного заранее опорного решения по определенному алгоритму симплекс-метода мы подсчитываем новое опорное решение, на котором значение целевой функции F не меньше, чем на старом. После ряда шагов мы приходим к опорному решению, которое является оптимальным планом.

Итак, симплексный метод вносит определенный порядок как при нахождении первого (исходного) базисного решения, так и при переходе к другим базисным решениям. Его идея состоит в следующем.

Имея систему ограничений, приведенную к общему виду, то есть к системе m линейных уравнений с n переменными (m < n), находят любое базисное решение этой системы, заботясь только о том, чтобы найти его как можно проще.

Если первое же найденное базисное решение оказалось допустимым, то проверяют его на оптимальность. Если оно не оптимально, то, осуществляется переход к другому, обязательно допустимому базисному решению.

Симплексный метод гарантирует, что при этом новом решении линейная форма, если и не достигнет оптимума, то приблизится к нему. С новым допустимым базисным решением поступают так же, пока не находят решение, которое является оптимальным. Если первое найденное базисное решение окажется недопустимым, то с помощью симплексного метода осуществляется переход к другим базисным решениям, которые приближают нас к области допустимых решений, пока на каком-то шаге решения либо базисное решение окажется допустимым и к нему применяют алгоритм симплексного метода, либо мы убеждаемся в противоречивости системы ограничений.

Таким образом, применение симплексного метода распадается на два этапа: нахождение допустимого базисного решения системы ограничений или установление факта ее несовместности; нахождение оптимального решения. При этом каждый этап может включать несколько шагов, соответствующих тому или иному базисному решению. Но так как число базисных решений всегда ограниченно, то ограниченно и число шагов симплексного метода.

Вычисления по симплекс-методу организуются в виде симплекс-таблиц которые являются сокращенной записью задачи линейного программирования в канонической форме. Перед составлением симплекс-таблицы задача должна быть преобразована, система ограничений приведена к допустимому базисному виду, c помощью которого из целевой функции должны быть исключены базисные переменные.

Для составления симплекс-таблицы во всех равенствах в условии задачи члены, содержащие переменные, переносятся в левую часть, свободные оставляются справа, т. е. задача записывается в виде системы равенств.

Далее эта система оформляется в виде симплекс-таблиц:

Первая симплекс-таблица подвергается преобразованию, суть которого заключается в переходе к новому опорному решению.

Алгоритм перехода к следующей таблице такой:

• · просматривается последняя строка (индексная) таблицы и среди коэффициентов этой строки выбирается наименьшее отрицательное число при отыскании max, либо наибольшее положительное при задачи на min. Если такового нет, то исходное базисное решение является оптимальным и данная таблица является последней;
• · просматривается столбец таблицы, отвечающий выбранному отрицательному (положительному) коэффициенту в последней строкеключевой столбец, и в этом столбце выбираются положительные коэффициенты. Если таковых нет, то целевая функция неограниченна на области допустимых значений переменных и задача решений не имеет;
• · среди выбранных коэффициентов столбца выбирается тот, для которого абсолютная величина отношения соответствующего свободного члена (находящегося в столбце свободных членов) к этому элементу минимальна. Этот коэффициент называется разрешающим, а строка в которой он находится ключевой;
• · в дальнейшем базисная переменная, отвечающая строке разрешающего элемента, должна быть переведена в разряд свободных, а свободная переменная, отвечающая столбцу разрешающего элемента, вводится в число базисных. Строится новая таблица, содержащая новые названия базисных переменных.

В результате получают новую симплекс-таблицу, отвечающую новому базисному решению.

Теперь следует просмотреть строку целевой функции (индексную), если в ней нет отрицательных значений (в задачи на нахождение максимального значения), либо положительных (в задачи на нахождение минимального значения) кроме стоящего на месте (свободного столбца), то значит, что оптимальное решение получено. В противном случае, переходим к новой симплекс таблице по выше описанному алгоритму.

Пример решения задачи линейного программирования симплекс методом.

F (x) = 57X₁ + 49X₂ + 46X₃

• 346X₁ + 266X₂ + 326X₃? 826,
• 196X₁ + 156X₂ + 136X₃? 726,
• 406X₁ + 466X₂ + 476X₃? 926 .

X₁, X₂, X₃? 0.

Решение :

Приводим задачу к каноническому виду для этого в левую часть первого ограничения вводим дополнительную переменную Х₆ с коэффициентом + 1.

В целевую функцию переменную Х₆ вводим с коэффициентом 0.

Получаем,.

F (x) = 57X₁ + 49X₂ + 46X₃ + 0X₄ + 0X₅ + 0X₆ max.

• 346X₁ + 266X₂ + 326X₃ + X₄ = 826,
• 196X₁ + 156X₂ + 136X₃ + X₅ = 726,
• 406X₁ + 466X₂ + 476X₃ + X₆ = 926 .

Находим начальное опорное решение. Для этого свободные переменные приравниваем к 0.

Х₁=Х₂=Х₃=0.

Получаем опорное решение Х₁= (0, 0, 0, 726, 826, 926).

Получаем опорное решение Х₁ с единичным базисом Б= (А₄, А₅, А₆).

Вычисляем оценки разложения векторов условий по базису опорного решения по формуле :

Д_к=С_б*Х_к-С_к, где С_б=(С₁, С₂, С₃… С_n) -это вектор коэффициентов целевой функции при базисных переменных.

Х_к=(Х_к1, Х_к2…Х_nк) — это вектор разложения соответствующего вектора А_к по базису опорного решения.

С_к— это коэффициент целевой функции при переменной Х_к.

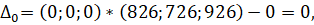
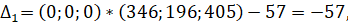
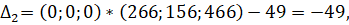
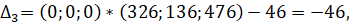
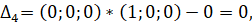
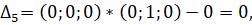
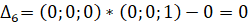
Оценки векторов, входящих в базис всегда равно 0. Опорное решение коэффициенты разложений и оценки разложения векторов условий по базису опорного решения записываются в симплексную таблицу.

В первом столбце под названием Б записываются векторы, входящие в базис опорного решения. Порядок записи этих векторов соответствуют разрешенных неизвестных в уравнениях ограничений.

Во втором столбце таблицы записывают коэффициент целевой функции для базисных переменных в том же порядке.

В 3 столбце таблицы записывают значения целевой функции на опорном решении f (Х₁). Начальное опорное решение не является оптимальным, т.к. задачи на максимум оценки Д₁ =-57, Д₂ = -49, Д₃ = -46.

По теореме об улучшении опорного решения, если задачи на максимум хотя бы один вектор имеет отрицательное значение, то можно найти новое опорное решение, на котором значений целевой функции будет больше.

Д₀=(0 ;0;57) * (30,2; 275,2; 2,3)-0= 131, 1.

Д₁=(0, 0; 57) * (0;0;1)-57 = 0.

Д₂= (0;0;57) * (- 26,6; -59,6; 1,1)-49 = 8.

Д_{3 =} (0;0;57) * (-89,2;-99,2; 1,2) -46 =22,4.

Д₄₌(0;0;57)* (1, 0, 0) — 0=0.

Д₅₌(0;0;57)* (0,1,0) — 0 =0.

Д₆₌(0;0;57)* (-0,692; -0, 392; 0, 002) — 0 = 0, 144.

Вводим А₁.

Выводим А₆.

Ответ: это решение является единственным оптимальным, т.к. для всех векторов не входящих в базис оценки положительный max f (x)=131, 1, при Х= (0; 8; 22, 4; 0; 0; 0, 114).