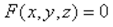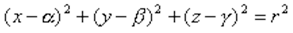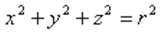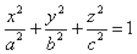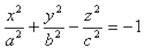Уравнение поверхности. 
Прямые и плоскости в пространстве

Уравнением данной поверхности (в выбранной системе координат) называется такое уравнение с тремя переменными которому удовлетворяют координаты каждой точки, лежащей на этой поверхности, и не удовлетворяют координаты никакой точки, не лежащей на ней.

Сфера

В декартовых прямоугольных координатах сфера, имеющая центр и радиус r, определяется уравнением:

Сфера радиуса r, центр которой находится в начале координат, имеет уравнение:

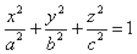
Эллипсоидом называется поверхность, которая в некоторой системе декартовых прямоугольных координат определяется уравнением:

Уравнение называется каноническим уравнением эллипсоида. Величины a, b, c полуоси эллипсоида. Если все они различны, эллипсоид называется трехосным; в случае, когда какие-нибудь две из них одинаковы, эллипсоид называется вытянутым, при a=b>c — сжатым. В случае, когда a=b=c, эллипсоид представляет собой сферу.

Гиперболоидами называются поверхности, которые в некоторой системе декартовых прямоугольных координат определяются уравнениями:

Гиперболоид, определяемый уравнением (1), называется однополостным;

уравнение прямая точка поверхность.

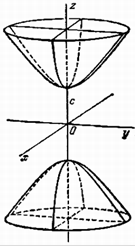
Гиперболоид, определяемый уравнением (2), — двуполостным.

уравнения (1) и (2) называются каноническими уравнениями соответствующих гиперболоидов. Величины a, b, c называются полуосями гиперболоида. В случае однополостного гиперболоида, заданного уравнением (1), только первые из них (а и b) показаны на рис. В случае двуполостного гиперболоида, заданного уравнением (2), одна из них (именно, с) показана на рис.

Гиперболоиды, определяемые уравнениями (1) и (2), при a=b являются поверхностями вращения.