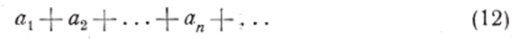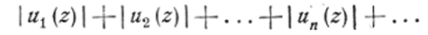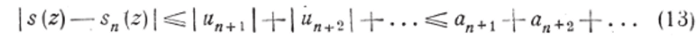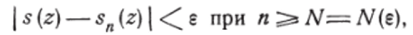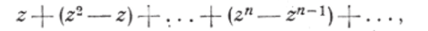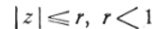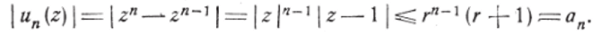Признак равномерно сходящегося ряда

Весьма часто можно заключить о равномерной сходимости ряда (5) на основании следующего простого признака:

если все члены (5) в области G удовлетворяют условию:

где а_п — постоянные положительные числа, причем числовой ряд.

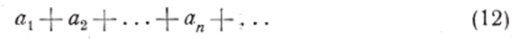
сходится, то данный ряд (5) сходится равномерно {и притом абсолютно) в области G. Действительно, ряд.

сходится во всякой точке г области G, так как его члены не больше соответствующих членов а_п сходящегося ряда (12). Следовательно, данный ряд (5) абсолютно сходится в каждой точке z области G. Обозначая через s (z) и s"(z) соответственно полную сумму ряда (5) и сумму первых п его членов, получим:

Так как ряд (12), по условию, сходится, то его остаточный член + л_л+2 + • • • будет меньше s, каково бы ни было е^>0, начиная с достаточно большого п^ N== N (b).

Таким образом, из неравенства (13) получаем:

независимо от точки z области О, что и доказывает равномерную сходимость ряда (5) в области G. В качестве примера рассмотрим ряд: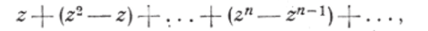

равномерную сходимость которого мы уже обнаружили при 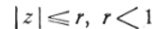(гл. И, § 2, и. 1). Здесь u_n(z) = zⁿ— zⁿ~^l, следовательно:

Так как ряд с общим членом а_п = г^п~¹ (г-j-l) при г<^1 сходится, как бесконечно убывающая геометрическая прогрессия, то на основании доказанного признака рассматриваемый ряд должен сходиться равномерно (и абсолютно) при г<^.