Множество положительных рациональных чисел как расширение множества натуральных чисел

Чтобы множество Q+ положительных рациональных чисел являлось расширением множества N натуральных чисел, необходимо выполнение ряда условий.

Первое условие — это существование между N и Q+ отношения включения. Докажем, что N Q+.

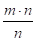
Пусть длина отрезка х при единичном отрезке е выражается натуральным числом т. Разобьем единичный отрезок на п равных частей. Тогда n-ая часть единичного отрезка будет укладываться в отрезке х точно раз, т. е. длина отрезка х будет выражена дробью. Значит, длина отрезка х выражается и натуральным числом т, и положительным рациональным числом. Но это должно п быть одно и то же число.

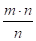
Поэтому целесообразно считать, что дроби вида являются записями натурального числа т. Следовательно, N Q+.

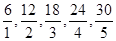
Так, например, натуральное число 6 можно представить в виде следующих дробей:, ,, ,, и т. д.

Отношение между множествами N и Q+ представлено на рисунке 28.

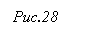
Числа, которые дополняют множество натуральных чисел до множества положительных рациональных, называются дробными.

Второе условие, которое должно быть выполнено при расширении множества натуральных чисел, — это согласованность операций, т. е. результаты арифметических действий, произведенных по правилам, существующим для натуральных чисел, должны совпадать с результатами действий над ними, но выполненных по правилам, сформулированным для положительных рациональных чисел. Нетрудно убедиться в том, что и это условие выполняется.

Пусть а и b — натуральные числа, — их сумма, полученная по правилам сложения в N. Вычислим сумму чисел а и b по правилу сложения в Q+.

Так как, , то.

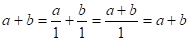
Третье условие, которое должно быть выполнено при расширении множества натуральных чисел — это выполнимость в Q+ операции, не всегда осуществимой в N. И это условие соблюдено: деление, которое не всегда выполняется в множестве N, в множестве Q+ выполняется всегда.

Сделаем еще несколько дополнений, раскрывающих взаимосвязи между натуральными и положительными рациональными числами.

1. Черту в записи дроби можно рассматривать как знак деления.

Действительно, возьмем два натуральных числа т и п и найдем их частное по правилу (4) деления положительных рациональных чисел:

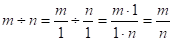
Обратно, если дана дробь, то ее можно рассматривать как частное натуральных чисел т и п .

2. Любую неправильную дробь можно представить либо в виде натурального числа, либо в виде смешанной дроби.

Пусть — неправильная дробь. Тогда т > п. Если т кратно п, то в этом случае дробь является записью натурального числа. Если число т не кратно п, то разделим т на п с остатком:, где. Подставим вместо т в запись и применим правило (1) сложения положительных рациональных чисел:

.

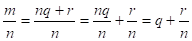
Так как , то дробь — правильная. Следовательно, неправильная дробь оказалась представленной в виде суммы натурального числа q и правильной дроби. Это действие называется выделением целой части из неправильной дроби. Например,.

Сумму натурального числа и правильной дроби принято записывать без знака сложения: т. е. вместо пишут и называют такую запись смешанной дробью.

Справедливо также утверждение: всякую смешанную дробь можно записать в виде неправильной дроби. Например:

.

Основными математическими объектами с незапамятных времен являются числа, множества и элементы множества, их свойства. Число — абстракция, используемая для количественной характеристики объектов. Возникнув ещё в первобытном обществе из потребностей счёта, понятие числа изменялось и обогащалось и превратилось в важнейшее математическое понятие. Письменными знаками (символами) для записи чисел служат цифры. Современная математика оперирует несколько другими математическими понятиями. Если внимательно проанализировать их суть, то они, в общем-то, являются эквивалентными или изоморфными понятиям «число», «множество», «отображение», «свойство».

В теоретико-множественном смысле числа являются классом множеств с определенными свойствами. Эти свойства выражаются через тип упорядоченности, размерность, топологические и метрические свойства основанных на них множеств. Основное свойство чисел — это их мощность, которая может быть конечной, счетной или континуальной. Соответственно, числа могут быть представителями любого класса множеств с подходящей мощностью. Даже множества с мощностью больше континуума можно представить как множество всех функций, определенных на числовом множестве. В этом проявляется универсальность понятия «число».

Другое важное свойство чисел — это ее размерность. Есть несколько классов чисел с различающимися свойствами. Есть линейные (одномерные) числа — это натуральные N, положительные N⁺, целые Z, рациональные R и вещественные Q числа. Есть составные многомерные или гиперкомплексные числа — это комплексные числа C, кватернионы H, бикватернионы B, невырожденные квадратные матрицы M, числа Клиффорда K и другие. Тензор (в том числе и вектор) в обычном понимании не является числом.

Интересным видом чисел являются гипердействительные числа. Они появляются в нестандартном анализе, использующем понятия «бесконечно малые» и «бесконечно большие» чисел как расширение множества действительных до этих «бесконечных» чисел.

Попробуем определить, что такое «число». Точнее, виды чисел.

Самыми простыми числами являются целые, рациональные, вещественные и комплексные числа. Они коммутативны, ассоциативны и дистрибутивны.

Основными видами чисел, обладающими похожими свойствами, являются четыре вида чисел. Это действительные числа, комплексные, кватернионы и октавы. Коммутативность умножения для последних двух видов чисел не выполняется. Но они все обладают алгебрами без делителей нуля.

Дальнейшие расширения чисел могут не иметь и свойство ассоциативности. Дистрибутивность соблюдается.

Основные виды чисел Натуральные числа, получаемые при естественном счёте; множество натуральных чисел обозначается N. Т.о. (иногда к множеству натуральных чисел также относят ноль, то есть N = {0, 1, 2, 3, …}). Натуральные числа замкнуты относительно сложения и умножения (но не вычитания или деления). Натуральные числа коммутативны и ассоциативны относительно сложения и умножения, а умножение натуральных чисел дистрибутивно относительно сложения.

Целые числа получаемые объединением натуральных чисел с множеством отрицательных чисел и нулём, обозначаются Z = {-2, -1, 0, 1, 2, …}. Целые числа замкнуты относительно сложения, вычитания и умножения (но не деления).

Рациональные числа — числа, представленные в виде дроби m/n (n? 0), где m — целое число, а n — натуральное число. Для рациональных чисел определены все четыре «классические» арифметические действия: сложение, вычитание, умножение и деление (кроме деления на ноль). Для обозначения рациональных чисел используется знак Q.

Действительные (вещественные) числа представляют собой расширение множества рациональных чисел, замкнутое относительно некоторых (важных для математического анализа) операций предельного перехода. Множество вещественных чисел обозначается R. Его можно рассматривать как пополнение поля рациональных чисел Q при помощи нормы, являющейся обычной абсолютной величиной. Кроме рациональных чисел, R включает множествоиррациональных чисел, не представимых в виде отношения целых. Кроме подразделения на рациональные и иррациональные, действительные числа также подразделяются на алгебраические и трансцендентные. При этом каждое трансцендентное число является иррациональным, каждое рациональное число — алгебраическим.

Комплексные числа, являющиеся расширением множества действительных чисел. Они могут быть записаны в виде z = x + iy, где i — т. н. мнимая единица, для которой выполняется равенство i² = -1. Комплексные числа используются при решении задач квантовой механики, гидродинамики, теории упругости и пр.

Для перечисленных множеств чисел справедливо следующее выражение: N? Z? Q? R? C.

Гипердействительные числа — это числа вида:

1) a + ?, где a — обычное число, a — бесконечно малое число;

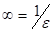
2)? = 1/? — бесконечно большое число.

Гипердействительные числа не являются числами в обычном понимании. Они применяются во многих разделах математики, особенно в дифференциальном и интегральном исчислениях, а также везде, где используются предельные числовые последовательности, даже при определении вещественных чисел.

Множество рациональных чисел является естественным обобщением множества целых чисел. Легко видеть, что если у рационального числа a = m/n знаменатель n = 1, то a = m является целым числом. В этой связи возникают некоторые обманчивые предположения. Во-первых, кажется, что рациональных чисел больше чем целых, на самом же деле и тех и других счётное число. Во-вторых, возникает предположение, что такими числами можно измерить абсолютно точно любое расстояние в пространстве. На самом деле, для этого используются вещественные числа, рациональных же чисел для этого недостаточно.

Виды дроби Правильной называется дробь, у которой модуль числителя меньше модуля знаменателя. Дробь, не являющаяся правильной, называется неправильной.

Например, дроби 3/5, 7/8 и ½ — правильные дроби, в то время как 8/3, 9/5, 2/1и 1/1 — неправильные дроби. Всякое целое число можно представить в виде неправильной обыкновенной дроби со знаменателем 1.

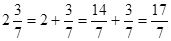
Дробь, записанная в виде целого числа и правильной дроби, называется смешанной дробью и понимается как сумма этого числа и дроби. Например,. В строгой математической литературе такую запись предпочитают не использовать из-за схожести обозначения смешанной дроби с обозначением произведения целого числа на дробь.

Несмотря на то, что рациональных чисел бесконечное множество и то, что мы можем записать только не бесконечно большие числа, можно считать, что мы можем записать любое рациональное число указанным выше способом, потому что любое рациональное число явно не бесконечное и запись ее будет содержать конечное число символов.

Высота дроби Высота обыкновенной дроби — то модуль суммы числителя и знаменателя этой дроби. Высота рационального числа — это модуль суммы числителя и знаменателя несократимой обыкновенной дроби, соответствующей этому числу.

Например, высота дроби (-15/6) равна 15 + 6 = 21. Высота же соответствующего рационального числа равна 5 + 2 = 7, так как дробь сокращается на 3.

Как следствие, множество рациональных чисел является счетным множеством. Дробь рациональное число нерациональное число Это множество обладает свойством непрерывности. Это означает, что между любыми неравными между собой числами можно найти третье число, не равное предыдущему. Более того, сечение рациональных чисел на две половинки может быть открытым по одной или обеим границам этого сечения.

Множество рациональных чисел является абелевой группой по операциям «сложение» и «умножение» по отдельности.

Множество рациональных чисел является полем по операциям «сложение» и «умножение».

Формальное определение Формально рациональные числа определяются как множество классов эквивалентности пар {(m, n) | m? Z, n? N} по отношению эквивалентности (m, n) ~ (m', n'), если m • n' = m' n. При этом операции сложения и умножения определяются следующим образом:

• (m₁, n₁) + (m₂, n₂) = (m₁, n₂ + m₂, n₁, n₁ • n₂),
• (m₁, n₁) • (m₂, n₂) = (m₁ • m₂, n₁ • n₂).

Свойства рациональных чисел Рациональные числа удовлетворяют шестнадцати основным свойствам, которые легко могут быть получены из свойств целых чисел.

• 1. Упорядоченность. Для любых рациональных чисел a и b существует правило, позволяющее однозначно идентифицировать между ними одно и только одно из трёх отношений: «» или «= «. Это правило называется правилом упорядочения и формулируется следующим образом: два неотрицательных числа a = ma/na и b = mb/nb связаны тем же отношением, что и два целых числа ma/nb и mb/na;два неположительных числа a и b связаны тем же отношением, что и два неотрицательных числа |b| и |a|; если же вдруг a неотрицательно, а b — отрицательно, то a >b.
• ?a, b? Q: a < b? b < a? a = b
• 2. Транзитивность отношения порядка. Для любой тройки рациональных чисел a, b и c если a меньше b и b меньше c, то a меньше c, а если a равно b и b равно c, то a равно c.
• ?x, y, z? Q: (x < y)? (y < z)> x < z (транзитивность порядка);
• 3. Операция сложения. Для любых рациональных чисел a и b существует так называемое правило суммирования, которое ставит им в соответствие некоторое рациональное число c. При этом само число c называется суммой чисел a и b и обозначается (a + b), а процесс отыскания такого числа называется суммированием. Правило суммирования имеет следующий вид: (m1/n1) + (m2/n2) = (m1 • n2 + m2 • n1)/(n1 • n2).
• ?a, b? Q: ?(a + b)? Q
• 4. Коммутативность сложения. От перемены мест рациональных слагаемых сумма не меняется.
• (?x, y? Q): (x + y) = (y + x)
• 5. Ассоциативность сложения. Порядок сложения трёх рациональных чисел не влияет на результат.
• (?x, y, z? Q): (x + y) + z = x + (y + z)
• 6. Наличие нуля. Существует рациональное число 0, которое сохраняет любое другое рациональное число при суммировании.
• (?0? Q) (?x? Q): (x + 0 = x)
• 7. Наличие противоположных чисел. Любое рациональное число имеет противоположное рациональное число, при суммировании с которым даёт 0.
• (?x, y? Q) ?(-x? Q): (x + (-x) = 0).
• 8. Связь отношения порядка с операцией сложения. К левой и правой частям рационального неравенства можно прибавлять одно и то же рациональное число.
• ?x, y, z? Q: (x < y) > (x + z) < y + z
• 9. Операция умножения. Для любых рациональных чисел a и b существует так называемое правило умножения, которое ставит им в соответствие некоторое рациональное число c. При этом само число c называется произведением чисел a и b и обозначается (a · b), а процесс отыскания такого числа также называется умножением. Правило умножения имеет следующий вид: ma/na · mb/nb = ma · mb / na · na.
• ?a, b ?Q: ?(a · b)? Q
• 10. Коммутативность умножения. От перемены мест рациональных множителей произведение не меняется.
• ?x, y? Q: (x • y) = (y • x);
• 11. Ассоциативность умножения. Порядок перемножения трёх рациональных чисел не влияет на результат.
• ?x, y, z? Q: (x • y) • z = x • (y • z);
• 12. Наличие единицы. Существует рациональное число 1, которое сохраняет любое другое рациональное число при умножении.
• ?1? Q{0}: ?x? Q: x • 1 = x;
• 13. Наличие обратных чисел. Любое рациональное число имеет обратное рациональное число, при умножении на которое даёт 1.
• ?x? Q{0}:?x-¹: x • x-¹ = 1.
• 14. Связь отношения порядка с операцией умножения. Левую и правую части рационального неравенства можно умножать на одно и то же положительное рациональное число.
• ?x, y, z? Q: (x < y)? (z > 0) > y • z < x • z
• 15. Дистрибутивность умножения относительно сложения. Операция умножения согласована с операцией сложения посредством распределительного закона:
  • (?x, y, z? Q: (x + y) • z = x • z + y • z
• 16. Аксиома Архимеда. Каково бы ни было рациональное число a, можно взять столько единиц, что их сумма превзойдёт a.

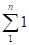
?a? Q ?n? N: > a

Дополнительные свойства Все остальные свойства, присущие рациональным числам, не выделяют в основные, потому что они, вообще говоря, уже не опираются непосредственно на свойства целых чисел, а могут быть доказаны исходя из приведённых основных свойств или непосредственно по определению некоторого математического объекта. Таких дополнительных свойств очень много. Здесь имеет смысл привести лишь некоторые из них.

Второе отношение порядка «>» также транзитивно.

?x, y, z? Q: (x > y)? (y > z)> x > z (транзитивность порядка);

Произведение любого рационального числа на ноль равно нулю.

?x? Q: x · 0 = 0;

Отсутствие делителей нуля.

Рациональные неравенства одного знака можно почленно складывать.

?a, b, c, d? Q: a > b? c > d > a + c > b + d

Множество рациональных чисел Q является полем (а именно, полем частных кольца целых чисел Z) относительно операций сложения и умножения дробей.

Каждое рациональное число является алгебраическим.

Математика в силу своей специфики предоставляет большие возможности для учителя в плане развития мышления детей. Развивать мышление учащихся можно при изучении, практически, любой математической темы. Мы остановились на рассмотрении долей и дробей, и именно это обусловило выбор темы нашего исследования: «Развитие мышления младших школьников в процессе пропедевтической работы по изучению дробей».