Геометрические построения. 
Математика народов Средней Азии, Ближнего и Среднего Востока

С нуждами землемерия, архитектуры, техники связаны разработки методов геометрических построений. Внук Сабита ибн Коры Ибрагим ибн Синан (908−946) в «Книге о построении трех (конических) сечений» рассматривает семь способов построения эллипса, гиперболы и параболы по точкам с помощью циркуля и линейки.

Абу Саид ас-Сиджизи (X-XI вв.) в «Трактате об описании конических сечений» применял для непрерывного построения всех трех конических сечений так называемый совершенный циркуль, одна из ножек которого при вращении может вытягиваться и сокращаться по длине отрезка прямоугольной образующей конуса от его вершины до точек сечения. На рис. 4 изображен совершенный циркуль, ножка АВ которого закреплена под углом б к плоскости бумаги, а ножка ВС переменной длины вращается вокруг ножки АВ под углом в.

При б > в сечение является эллипсом, при б =в — параболой, а при б < в — ветвью гиперболы.

Непрерывному построению эллипса с помощью нити, закрепленной в его фокусах (так называемый способ садовника), посвящен написанный в IX в. Трактат одного из братьев Бану Мусса ал-Хасана «Об удлиненном круге». Большое число геометрических построений изложено в «Книге о том, что необходимо ремесленнику из геометрических представлений» Абу-л-Вафы ал-Бузджани (недавно выяснилось, что большая часть этой книги текстуально совпадает с написанной на 50 лет ранее книги знаменитого философа Абу Насыра ал-Фараби (ок 870 — 950)).

Из геометрических задач Абу-л-Вафы отметим остроугольное построение квадрата, равновеликого трем равным квадратам, путем раскроя этих квадратов: два из них делятся диагонально пополам, полученные треугольники приставляются к сторонам третьего квадрата.

Тогда фигура EFGH-искомый квадрат, который получается отрезанием выступающих частей треугольников и вставлением их на место равных им частей квадрата EFGH, незаполненных треугольниками.

Из других методов решения Абу-л-Вафом этой задачи следует отметить построение стороны утроенного квадрата как диагонали куба, построенного на одном из малых квадратов. Особенно важно замечание его к последнему методу: «точно так же обстоит дело, если мы хотим построить квадрат, состоящий более чем из трех или менее чем из трех квадратов», который для n>3 квадратов означает мысленное построение диагонали n-мерного куба, построенного на данном квадрате. Именно в эту эпоху на востоке получили распространение геометрические названия степеней выше третьей: квадрато-квадрат, квадрато-куб, кубо-куб …, являющиеся переводами терминов Диофанта и их обобщениями. Эти термины были известны Абу-л-Вафе, которому принадлежит комментарий к «Арифметике» Диофанта.

Используются вычислительные методы, тригонометрические приемы. С большой точностью вычисляются правильные многоугольники и многогранники.

Ярким примером искусного применения вычислительной техники служит «Трактат об окружности» ал-Каши, в котором длина окружности вычислена как среднее арифметическое периметров вписанного и описанного правильных многоугольников с числом сторон. При этом им получено значение числа, где неверна последняя цифра 5, а надо поставить вместо нее число 38.

Подобная точность была вновь достигнута лишь 150 лет спустя А. ван Рооменом, который воспользовался вписанным и описанным 2³⁰-угольниками.

Заметим, что математики стран ислама уже высказывали мысль об иррациональности числафакт, доказанный только в XVIII в. Ламбертом и Лежандром.

Вычисление стороны правильного пятиугольника.

Из «Измерения пятиугольника и десятиугольника Абу Камила (ок 900 г.)».

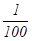
Рассмотрим в качестве образца применения алгебры к решению задач геометрии вычисление стороны правильного пятиугольника, вписанного в данную окружность. Правильные 5-ти и 10-ти угольники были изучены еще в древней Греции. Я начинаю с определения меры (хорды) одно пятой окружности, диаметр которой известен. Пусть дан круг и пусть его диаметр 10 в числах. АВСDЕ — вписанный 5-ти угольник с равными сторонами и углами. Если ты хочешь знать меру каждой стороны этого пяти угольника, то проведем линию СHD, отсекаемую две пятые окружности. Будем считать линию ED вещью (неизвестная). Так как квадрат ED равен плоской фигуре EH на EF (т.е. прямоугольник на отрезках EH и EF), то EH равна 1/10 квадрата и CH равна корню из квадрата без квадрато-квадрата. Но CH равна Ѕ CD, поэтому CD равна корню из 4 квадратов без 2/5 от 1/10 квадрато-квадрата. Действительно, так как и EF = 10, из равенства.

ED²=EH•EF.

EH=x²/10,.

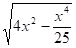
CD=2CH= .

Но плоская фигура АС на BD равна квадрату CD. Но квадрат СD равен 4квадратам без 2/5 1/10 квадрато-квадрата, если вычесть отсюда плоскую фигуру AD на BC, равную квадрату ED, т. е. квадрату, то останется плоская фигура АВ на CD равная 3 квадратам без 2/5 1/10 квадрато-квадрата. Раздели это на АВ, то есть вещь, в частном получим: СD равна 3 вещам без 2/5 1/10 кубов. Умножь это на себя, получится: квадрат CD = 9 квадратам и 1/625 кубо-куба без 6/25 квадрато-квадрата, но это равно 4 квадратам без 2/5 1/10 квадрато-квадрата. Вспомни это, получится 5/25 квадрато-квадрата равны 5 квадратам и 1/625 кубо-куба. Раздели все это на квадрат, получится 1/5 квадрата, равная 5 и 1/625 квадрато-квадрата; вспомни это так, чтобы получился квадрато-квадрата, для чего умножь это на 625, получится квадрато-квадрат и 3125 равны 125 квадратам.

Действительно, равенство.

AB•CD+АD•BС=CD²

можно записать в виде:

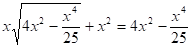
откуда (*).

Далее говорится: раздвой квадраты, получится 62 ½, умножь это на себя, получится 3906 ¼, вычти из этого 3125, останется 781 ј, корень из этого вычти из 62 Ѕ, корень из остатка линия ED, являющаяся одной из сторон пятиугольника.

Действительно из (*) найдем :

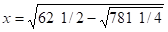
Теория параллельных.

Теорией параллельных на протяжении IX—XIV вв.еков занимались многие арабские математики. Напомним постулат параллельных Евклида (если прямая образует с двумя другими прямыми, лежащими в одной плоскости, внутренние односторонние углы, в сумме меньше двух прямых, то эта прямая при достаточном продолжении пересекается с той стороны, где эта сумма меньше 2-х прямых).

Ал-Джаухари в «Совершенной книге „Начала“» опирался на неявно предполагаемое допущение, равносильное доказываемому постулату: если при пересечении двух прямых какой либо третьей накрест лежащие углы равны, то тоже имеет место при пересечении тех же двух прямых любой другой прямой. Он доказал в качестве теоремы предложение: через любую точку внутри любого данного угла можно провести прямую пересекающую обе его стороны.

Два трактата, посвященные доказательству пятого постулата, принадлежит Сабиту ибн Корре. В «Книге о доказательстве известного постулата Евклида» он основывается на предположении, что если две прямые удаляются друг от друга с одной стороны, они обязательно приближаются с другой стороны. С помощью этого утверждения он доказывает существование параллелограмма, после чего доказывается пятый постулат. Другой трактат его называется в «Книге о том, что две линии, проведенные под углами, меньшими двух прямых, встретятся», в котором он исходит из существования равноотстоящих прямых, с помощью чего доказывает начало существования прямоугольника. Но существование равноотстоящих прямых на плоскости не постулируется и пытается вывести его из представления о «простом движении», т. е. о равномерном поступательном движении вдоль прямой. Он (ибн Корра) считает при таком движении все движущиеся точки описывают прямые линии.

Ибн ал-Хайсам в трактате «О разрешении сомнений в книге Евклида „Начала“», исходит из того, что две пересекающиеся прямые не могут быть параллельны одной прямой, т. е. что из одной точки нельзя провести двух параллелей к одной прямой. В «Книге комментариев к введениям книги» Евклида «Начала» Ибн ал-Хайсам использует тоже представление о простом «движении». С помощью которого он устанавливает, что конец отрезка, перпендикулярного к прямой, вдоль которой происходит движение, описывает прямую, которая, т.о., является равноотстоящей от данной прямой. Далее доказывается существование прямоугольника для чего рассматривается четырехугольник с тремя прямыми углами и три гипотезы о четвертом угле этого четырех угольника: либо этот угол острый, либо тупой, либо прямой.

Теперь мы знаем, что гипотеза острого угла имеет место в геометрии Лобачевского, в котором выполняются все аксиомы геометрии Евклида, кроме пятого постулата. Гипотеза тупого угла выполняется в неевклидовой геометрии Римана (Эллиптическая геометрия) и на сфере, если считать большие круги сферы прямыми линиями.

Гипотеза прямого угла имеет место в геометрии Евклида. Ибн-ал-Хайсам опровергает первые две гипотезы с помощью «доказанного» им существованием равноотстоящих прямых.

Омар Хайям в «Комментариях к трудностям во введениях книги Евклида» считает, что в геометрию нельзя вводить движение. Он исходит из принципа: две сходящиеся прямые пересекаются и невозможно, чтобы две сходящиеся прямые расходились в направлении схождения. Он рассматривает четырехугольник с двумя равными сторонами, перпендикулярными к основанию. Углы, прилегающие к четвертой стороне равны между собой. Рассматриваются три гипотезы о величине этих углов.

Омар Хайям так же приходит к существованию прямоугольника. Арабские математики сделали несколько выдающихся открытий: установили двустороннюю зависимость между этим постулатом и величиной суммы углов четырехугольника, треугольника; установили логическую эквивалентность ряда предложений теории параллельных; применили для опровержения гипотез острого и тупого углов способ приведения к противоречию и т. д. О. Хайям получил некоторые предложения, по существу принадлежащие к первым теоремам неевклидовых геометрий Лобачевского и Римана.