Методы решения уравнений в частных производных

уравнение лагранж производная вариационный Основные понятия и методы, используемые при конечно-разностном решении уравнений в частных производных. Основой метода конечных разностей является дискретизация — замена непрерывной области совокупностью изолированных точек (сеткой), причем решение уравнений ищется лишь в этих точках (узлах сетки).

Производные аппроксимируются конечными разностями и решение уравнений в частных производных сводится к решению системы алгебраических уравнений.

Основные особенности получающейся системы алгебраических уравнений определяются типом исходного уравнения (или системы уравнений) в частных производных. Стационарные задачи обычно сводятся к системам алгебраических уравнений, которые приходится решать одновременно во всей области, учитывая заданные граничные условия. Нестационарные (маршевые) задачи часто сводятся к алгебраическим уравнениям, которые можно решать последовательно.

Основные понятия теории разностных схем

Пусть в некоторой области D поставлена некоторая дифференциальная краевая задача, определяемая дифференциальным уравнением и краевыми (граничными) условиями.

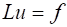
(1).

где через обозначен некоторый заданный дифференциальный оператор, действующий на искомую функцию, через — правая часть. Примем, что оператор включает как дифференциальное уравнение, так и граничные условия.

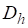
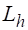
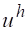
На некоторой разностной сетке строим разностный оператор, действующий на сеточную функцию .

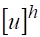
Обозначим через таблицу значений искомого решения в узлах сетки. Тогда соответствующая (1) разностная краевая задача (разностная схема) запишется в виде.

. (2).

Определение 1:

Будем говорить, что решение разностной краевой задачи (2) при сгущении сетки сходится к решению дифференциальной краевой задачи (1), если.

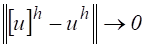
при, т. е. если норма разности точного и приближенного решений стремится к нулю при стремлении к нулю шага разностной сетки.

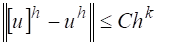
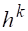
Если, сверх того, выполнено неравенство, где , — некоторые постоянные, не зависящие от, то будем говорить, что имеет место сходимость порядка или, что разностная схема имеет — й порядок точности.

В этом определении — проекция точного решения задачи (1) на сетку (- сеточная функция, компоненты которой есть значения точного решения в узлах сетки).

Предположим, что разностная задача (2) имеет единственное решение .

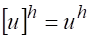
Если бы при подстановке в левую часть (2) вместо сеточной функции проекции точного решения на сетку — равенство (2) оказалось бы в точности выполненным, то ввиду единственности решения имело бы место равенство, идеальное с точки зрения сходимости.

Это означало бы, что решение разностной задачи (2) совпадает с искомой сеточной функцией, которую мы условились считать точным решением.

Однако, как правило, систему (2) не удается выбрать так, чтобы в точности ей удовлетворяла. При подстановке в уравнение (2) возникает некоторая невязка:

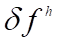
Величина называется невязкой, и при подстановке точного решения уравнения (1) в оператор имеем.

Определение 2:

Будем говорить, что разностная схема (2) аппроксимирует исходную дифференциальную задачу (1) на решении, если.

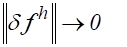
при, т. е. норма невязки стремится к нулю при стремлении к нулю шага разностной сетки.

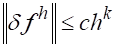
Если, сверх того, имеет место неравенство ,.

где , — некоторые постоянные, не зависящие от, то будем говорить, что имеет место аппроксимация порядка или порядка относительно величины .

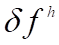
В случае аппроксимации можно считать, что уравнение (3) которому удовлетворяет, получается из уравнения (2) путем прибавления к правой части некоторой малой (при малом) добавки .

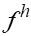
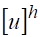
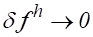
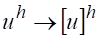
Следовательно, если решение задачи (2) устойчиво относительно возмущения правой, т. е. мало изменяется при малом изменении правой части, то решение задачи (2) и решение задачи (3) отличаются мало, так что из аппроксимации при следует сходимость, т. е. при .

Определение 3:

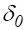
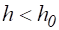
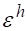
Будем называть разностную схему (2) устойчивой, если существуют такие постоянные и, что при любом и любой сеточной функции, такой, что разностная задача.

.

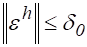
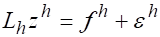
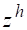
полученная из (2) добавление к правой части возмущения имеет место и имеет только одно решение, причем справедлива оценка.

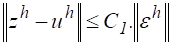
(4).

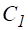
где — некоторая постоянная, не зависящая от .

Последнее неравенство означает, что малое возмущение правой части разностной схемы (2) вызывает равномерно относительно малое возмущение решения .

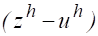
Теорема (теорема Лакса о сходимости):

Пусть разностная схема (2) аппроксимирует задачу (1) на решении с порядком и устойчива.

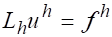
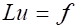
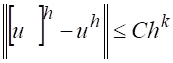
Тогда решение разностной задачи сходится к решению дифференциальной задачи, причем имеет место оценка, где — некоторая постоянная, не зависящая от .

Эта теорема позволяет свести вопрос о важнейшей с практической точки зрения проблемы исследования сходимости к вопросу исследования аппроксимации и устойчивости.

Заметим, что оба этих свойства разностных схем являются независимыми друг от друга.

Установить устойчивость разностной схемы с использованием данного выше определения на практике весьма затруднительно. Поэтому предложен ряд способов исследования устойчивости, позволяющих получить достаточные, а в ряде случаев необходимые и достаточные условия устойчивости разностных схем.

Прежде, чем рассматривать вариационный принципа Лагранжа, сначала рассмотрим энергию деформации упругого тела.