«Хи-квадрат» в задачах статистического анализа данных

Статистические методы анализа данных применяются практически во всех областях деятельности человека. Их используют всегда, когда необходимо получить и обосновать какие-либо суждения о группе (объектов или субъектов) с некоторой внутренней неоднородностью.

Современный этап развития статистических методов можно отсчитывать с 1900 г., когда англичанин К. Пирсон основал журнал «Biometrika». Первая треть ХХ в. прошла под знаком параметрической статистики. Изучались методы, основанные на анализе данных из параметрических семейств распределений, описываемых кривыми семейства Пирсона. Наиболее популярным было нормальное распределение. Для проверки гипотез использовались критерии Пирсона, Стьюдента, Фишера. Были предложены метод максимального правдоподобия, дисперсионный анализ, сформулированы основные идеи планирования эксперимента.

Распределение «хи-квадрат» является одним из наиболее широко используемых в статистике для проверки статистических гипотез. На основе распределения «хи-квадрат» построен один из наиболее мощных критериев согласия — критерий «хи-квадрата» Пирсона.

Критерием согласия называют критерий проверки гипотезы о предполагаемом законе неизвестного распределения.

Критерий ч2 («хи-квадрат») используется для проверки гипотезы различных распределений. В этом заключается его достоинство.

Расчетная формула критерия равна.

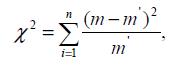
где m и m' - соответственно эмпирические и теоретические частоты рассматриваемого распределения;

n — число степеней свободы.

Для проверки нам необходимо сравнивать эмпирические (наблюдаемые) и теоретические (вычисленные в предположении нормального распределения) частоты.

При полном совпадении эмпирических частот с частотами, вычисленными или ожидаемыми S (Э — Т) = 0 и критерий ч2 тоже будет равен нулю. Если же S (Э — Т) не равно нулю это укажет на несоответствие вычисленных частот эмпирическим частотам ряда. В таких случаях необходимо оценить значимость критерия ч2, который теоретически может изменяться от нуля до бесконечности. Это производится путем сравнения фактически полученной величины ч2ф с его критическим значением (ч2st).Нулевая гипотеза, т. е. предположение, что расхождение между эмпирическими и теоретическими или ожидаемыми частотами носит случайный характер, опровергается, если ч2ф больше или равно ч2st для принятого уровня значимости (a) и числа степеней свободы (n).

Распределение вероятных значений случайной величины ч2 непрерывно и ассиметрично. Оно зависит от числа степеней свободы (n) и приближается к нормальному распределению по мере увеличения числа наблюдений. Поэтому применение критерия ч2 к оценке дискретных распределений сопряжено с некоторыми погрешностями, которые сказываются на его величине, особенно на малочисленных выборках. Для получения более точных оценок выборка, распределяемая в вариационный ряд, должна иметь не менее 50 вариантов. Правильное применение критерия ч2 требует также, чтобы частоты вариантов в крайних классах не были бы меньше 5; если их меньше 5, то они объединяются с частотами соседних классов, чтобы в сумме составляли величину большую или равную 5. Соответственно объединению частот уменьшается и число классов (N). Число степеней свободы устанавливается по вторичному числу классов с учетом числа ограничений свободы вариации.

Так как точность определения критерия ч2 в значительной степени зависит от точности расчета теоретических частот (Т), для получения разности между эмпирическими и вычисленными частотами следует использовать неокругленные теоретические частоты.

В качестве примера возьмем исследование, опубликованное на сайте, который посвящен применению статистических методов в гуманитарных науках.

Критерий «Хи-квадрат» позволяет сравнивать распределения частот вне зависимости от того, распределены они нормально или нет.

Под частотой понимается количество появлений какого-либо события. Обычно, с частотой появления события имеют дело, когда переменные измерены в шкале наименований и другой их характеристики, кроме частоты подобрать невозможно или проблематично. Другими словами, когда переменная имеет качественные характеристики. Так же многие исследователи склонны переводить баллы теста в уровни (высокий, средний, низкий) и строить таблицы распределений баллов, чтобы узнать количество человек по этим уровням. Чтобы доказать, что в одном из уровней (в одной из категорий) количество человек действительно больше (меньше) так же используется коэффициент Хи-квадрат.

Разберем самый простой пример.

Среди младших подростков был проведён тест для выявления самооценки. Баллы теста были переведены в три уровня: высокий, средний, низкий. Частоты распределились следующим образом:

Высокий (В) 27 чел.

Средний © 12 чел.

Низкий (Н) 11 чел.

Очевидно, что детей с высокой самооценкой большинство, однако это нужно доказать статистически. Для этого используем критерий Хи-квадрат.

Наша задача проверить, отличаются ли полученные эмпирические данные от теоретически равновероятных. Для этого необходимо найти теоретические частоты. В нашем случае, теоретические частоты — это равновероятные частоты, которые находятся путём сложения всех частот и деления на количество категорий.

В нашем случае:

(В + С + Н)/3 = (27+12+11)/3 = 16,6.

Формула для расчета критерия хи-квадрат:

ч2 = ?(Э — Т)І / Т Строим таблицу:

Находим сумму последнего столбца:

ч2= 9,64.

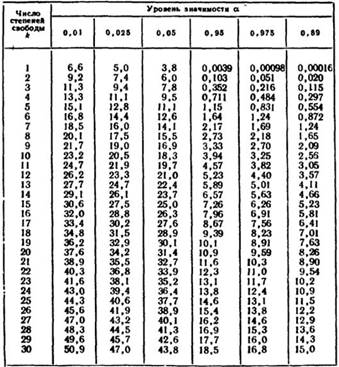
Теперь нужно найти критическое значение критерия по таблице критических значений (Таблица 1 в приложении). Для этого нам понадобится число степеней свободы (n).

n = (R — 1) * (C — 1).

где R — количество строк в таблице, C — количество столбцов.

В нашем случае только один столбец (имеются в виду исходные эмпирические частоты) и три строки (категории), поэтому формула изменяется — исключаем столбцы.

n = (R — 1) = 3−1 = 2.

Для вероятности ошибки p?0,05 и n = 2 критическое значение ч2 = 5,99.

Полученное эмпирическое значение больше критического — различия частот достоверны (ч2= 9,64; p?0,05).

Как видим, расчет критерия очень прост и не занимает много времени. Практическая ценность критерия хи-квадрат огромна. Этот метод оказывается наиболее ценным при анализе ответов на вопросы анкет.

Разберем более сложный пример.

К примеру, психолог хочет узнать, действительно ли то, что учителя более предвзято относятся к мальчикам, чем к девочкам. Т. е. более склонны хвалить девочек. Для этого психологом были проанализированы характеристики учеников, написанные учителями, на предмет частоты встречаемости трех слов: «активный», «старательный», «дисциплинированный», синонимы слов так же подсчитывались.

Данные о частоте встречаемости слов были занесены в таблицу:

Для обработки полученных данных используем критерий хи-квадрат.

Для этого построим таблицу распределения эмпирических частот, т. е. тех частот, которые мы наблюдаем:

Теоретически, мы ожидаем, что частоты распределятся равновероятно, т. е. частота распределится пропорционально между мальчиками и девочками. Построим таблицу теоретических частот. Для этого умножим сумму по строке на сумму по столбцу и разделим получившееся число на общую сумму (s).

Итоговая таблица для вычислений будет выглядеть так:

ч2 = ?(Э — Т)І / Т.

n = (R — 1),.

где R — количество строк в таблице.

В нашем случае хи-квадрат = 4,21; n = 2.

По таблице критических значений критерия находим: при n = 2 и уровне ошибки 0,05 критическое значение ч2 = 5,99.

Полученное значение меньше критического, а значит принимается нулевая гипотеза.

Вывод: учителя не придают значение полу ребенка при написании ему характеристики.