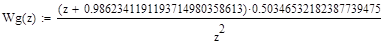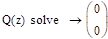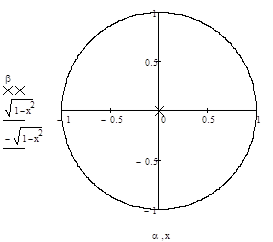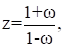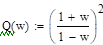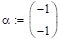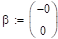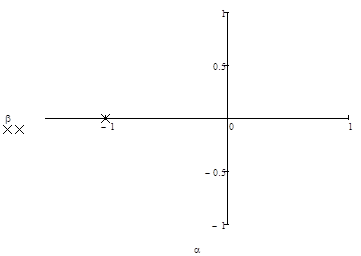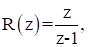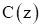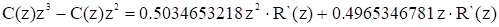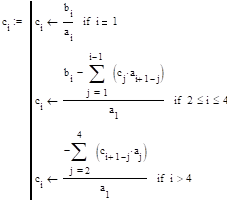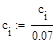Анализ дискретной СПР с переходным процессом конечной длительности
Определим корни характеристического полинома и изобразим их в плоскости «w». На рисунке 12 представлен переходный процесс конечной длительности. Система устойчива так как корни находятся в левой полуплоскости. Определим показатели качества по графику переходного процесса: Принимая что z=(n+1)T0, тогда разностное уравнение примет вид: Рисунок 12 — переходный процесс конечной длительности. Решение… Читать ещё >
Анализ дискретной СПР с переходным процессом конечной длительности (реферат, курсовая, диплом, контрольная)
Определение передаточной функции дискретной СПР
Желаемая передаточная функція системы с D (z):
.
Проверка устойчивости дискретной СПР по корням характеристического уравнения в плоскостях «z» и «w».
Результаты проверки устойчивости в плоскости «z» проведенные с помощью Mathcad приведены на рисунке 10.
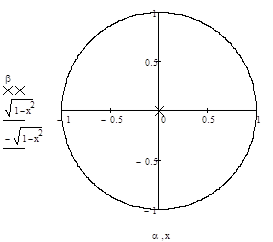
Рисунок 10 — Результаты расчетов.
Система устойчива так как корни находятся в середине окружности единичного радиуса.
Определим корни характеристического полинома и изобразим их в плоскости «w».
Проведем подстановку:
Тогда результат расчетов приведен на рисунке 11.
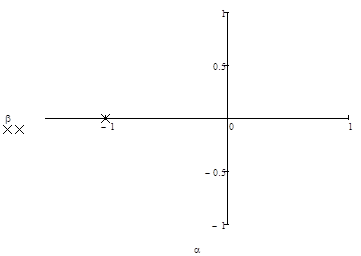
Рисунок 11 — Результат расчетов.
Система устойчива так как корни находятся в левой полуплоскости.
Нахождение уравнения переходного процесса и показателей качества при реакции дискретной СПР на единичное ступенчатое воздействие.
Выполним построение переходного процесса в цифровой СПР по разностному уравнению.
а выходная реакция:
Найдем :
.
По последнему выражению составляем уравнение:
.
Принимая что z=(n+1)T0, тогда разностное уравнение примет вид:
.
Принимая k=(n+3)Т0, обращаем выражение в прошлое.
Решение разностного уравнения приведено в таблице 2.
Таблица 2 — Решение разностного уравнения
k. | С (k-1). | R (k-1). | R (k-2). | Ck. | Ck/0,07. | |
0,503 465. | 0,496 535. | |||||
0,503 465. | 0,503 465. | 7,192 362. | 0,92. | |||
0,503 465. | 0,496 535. | 14,28 571. | 0,184. | |||
14,28 571. | 0,276. | |||||
14,28 571. | 0,368. | |||||
14,28 571. | 0,0046. | |||||
14,28 571. | 0,552. | |||||
14,28 571. | 0,644. | |||||
14,28 571. | 0,736. | |||||
14,28 571. | 0,828. | |||||
14,28 571. | 0,0092. |
На рисунке 12 представлен переходный процесс конечной длительности.
Рисунок 12 — переходный процесс конечной длительности.
Проведем тот же расчет в Mathcad:
Рисунок 13 — Решение в Mathcad.
Построим переходной процесс дискретной СПР в среде Matlab Simulink. mathcad регулятор ток Математическая модель системы представлена на рисунке 14.
Рисунок 14 — Математическая модель.
Результат моделирования представлен на рисунке 15.
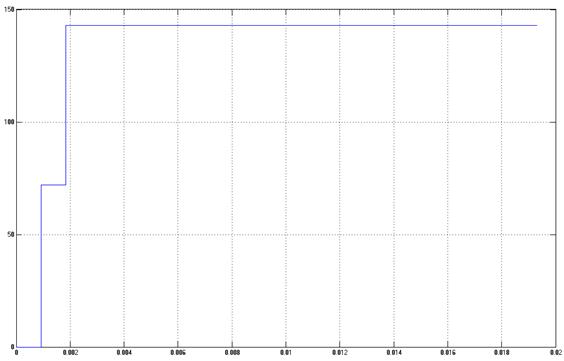
Рисунок 15 — График переходного процесса дискретной СПР при реакции на единичное ступенчатое воздействие.
Определим показатели качества по графику переходного процесса:
- — Время регулирования tо=0.184 с;
- — Перерегулирование .
Исходя из вида переходных процессов можно сделать вывод что СПР с дискретным регулятором конечной длительности переходного процесса имеет явные преимущества перед аналоговой СПР.