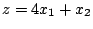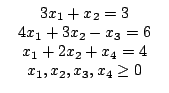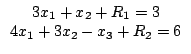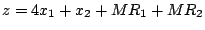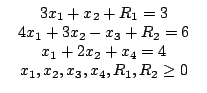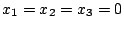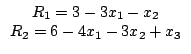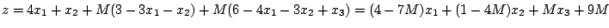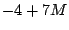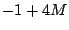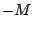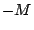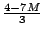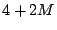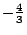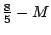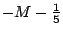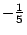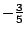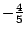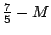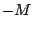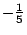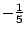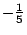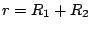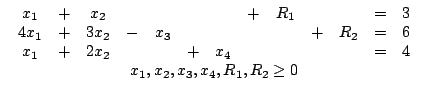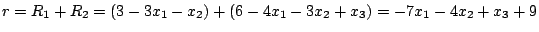Искусственное начальное решение

Для получения начального базисного решения мы использовали остаточные переменные. Однако когда исходное ограничение записано в виде равенства или имеет знак, нельзя сразу же получить НДБР. Поэтому были разработаны два метода, в которых используется «штрафование» искусственных переменных.

Метод больших штрафов (М-метод).

Рассмотрим линейную модель, приведённую к стандартной форме:

Минимизировать.

при ограничениях.

В первом и втором уравнениях нет переменных, исполняющих роль остаточных. Поэтому введём в каждое из этих уравнений по одной из искусственных переменных R1 и R2:

За использование этих переменных в составе целевой функции можно ввести штраф, приписывая им достаточно большой положительный коэфффициент. Получим линейную модель:

Минимизировать.

при ограничениях.

Теперь если.

то начальное допустимое решение:

Метод оптимизации, направленный на нахождение минимального значения, приведёт к тому, что переменные R1 и R2 в оптимальном решении обратятся в нуль.

Необходимо переформулировать условие задачи, чтобы представить процесс решения в удобной табличной форме. Подставив в целевую функцию полученные из соответствующих ограничений выражения для искусственных переменных.

получим выражение для :

Решение представлено в сводной таблице:

Итерация.		Решение.	Отно-шение.
	;
	;
	;
	;
	;
	;
	;
	;

Т.к. целевая функция минимизируется, переменные, включаемые в базис, должны иметь наибольшие положительные коэффициенты вуравнении. Оптимум достигается, когда все небазисные переменные имеют коэффициенты вуравнении. Оптимальному решению соответствует точка.

.

Т.к. в оптимальном решении отсутствуют искусственные переменные, имеющие положительное значение, то данное решение — допустимое оптимальное решение задачи в её стандартной постановке.

Двухэтапный метод Этап 1. Вводятся искусственные переменные, необходимые для получения стартовой точки. Записывается новая целевая функция, предусматривающая минимизацию суммы искусственных переменных при исходных ограничениях, видоизменённых за счёт искусственных переменных. Если минимальное значение новой целевой функции равно нулю (т.е. все искусственные переменные в оптимуме равны нулю), то исходная задача имеет допустимое решение и переходим к Этапу 2.

Этап 2. Оптимальное базисное решение, полученное на Этапе 1, используется в качестве начального условия исходной задачи.

Рассмотрим на примере.

Этап 1.

Минимизация.

при ограничениях.

Т.к., можно переходить к Этапу 2.

Этап 2. Исходную задачу сформулируем следующим образом:

Минимизировать при ограничениях.

Теперь, приравняв x3=0, получим НДБР.

Для решения задачи необходимо подставить в целевую функцию выражения для базисных переменных x1 и x2: