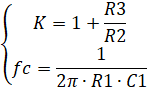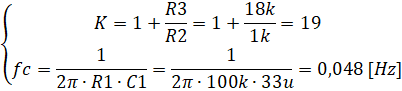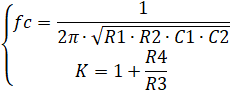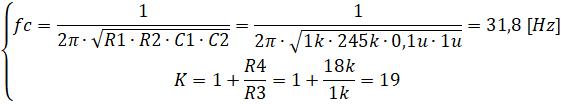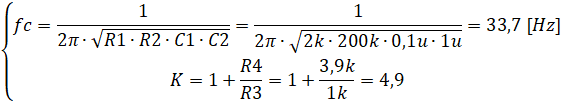Фильтр верхних частот. 
Расчет и моделирование

Зададим частоту среза fc=0,05 Гц. Выбирем неинвертирующий фильтр верхних частот первого порядка.

Исходя из рассуждений, описанных выше, коэффициент усиления фильтра примем 20.

Рассчитаем элементы схемы. Основные соотношения:

Выберем (в соответствии с «ГОС 28 884−90 Ряды предпочтительных значений для резисторов и конденсаторов»):

R1=100 [кОм];

R2=1 [кОм];

R3=18 [кОм];

C1=33 [мкФ].

Проверим подобранные параметры:

Промоделируем выбранный ФВЧ в среде MicroCap.

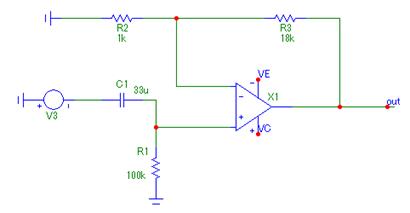
Рис. 12. Неинвертирубщий фильтр верхних частот в среде MicroCap.

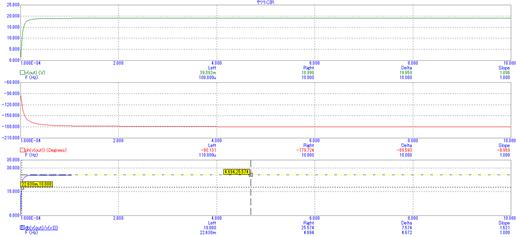
Рис. 13. Частотный анализ ФВЧ в среде MicroCap.

Фильтр нижних частот. Расчет и моделирование Частоту среза фильтра нижних частот выберем, исходя из полосы частот исследуемого сигнала. Примем частоту среза равную fc=30 Гц.

Для реализации выберем фильтр Баттерворта второго порядка.

Основные соотношения:

ФНЧ1.

Коэффициент усиления: 20.

Определим номиналы элементов схемы (в соответствии с «ГОС 28 884−90 Ряды предпочтительных значений для резисторов и конденсаторов»):

R1=1 [кОм];

R2=245 [кОм];

R3=1 [кОм];

R4=18 [кОм];

C1=0,1 [мкФ];

C2=1 [мкФ].

Проверим, подходят ли выбранные элементы:

Промоделируем рассчитанный фильтр в среде MicroCap.

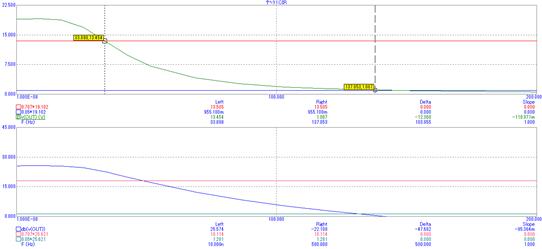
Рис. 15. Частотный анализ ФНЧ в среде MicroCap

ФНЧ2.

Коэффициент усиления данного фильтра: 5.

Определим номиналы элементов схемы (в соответствии с «ГОС 28 884−90 Ряды предпочтительных значений для резисторов и конденсаторов»):

R1=2 [кОм];

R2=200 [кОм];

R3=1 [кОм];

R4=3,9 [кОм];

C1=0,01 [мкФ];

C2=1 [мкФ].

Проверим, подходят ли выбранные элементы:

Промоделируем рассчитанный фильтр в среде MicroCap.

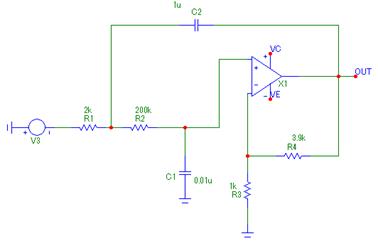
Рис. 16. Фильтр нижних частот второго порядка в среде MicroCap.

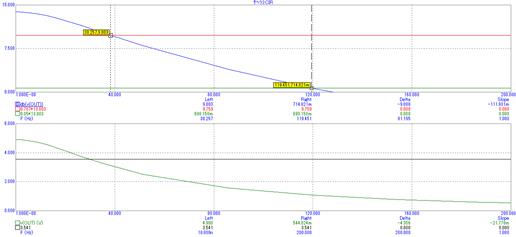
Рис. 17. Частотный анализ ФНЧ в среде MicroCap