Фильтрующий алгоритм. 
Алгоритм планирования пути на местности

Принцип динамического планирования Беллмана можно выразить фразой: «любая часть оптимальной траектории оптимальна». В частности, для любой промежуточной точки оптимального маршрута минимальна сумма затрат от стартового множества до данной точки. На основе принципа Беллмана можно предложить следующий вариант алгоритма решения общей задачи оптимального планирования пути. Начиная от точек стартового множества, строится веер оптимальных траекторий до тех пор, пока некоторая оптимальная траектория не достигнет какой-либо конечной точки. На каждом шаге алгоритма запоминается оптимальное направление перехода в текущую точку (шаговое управление на предшествующем шаге), что позволяет при достижении конечной точки восстановить весь оптимальный маршрут.

В предлагаемом алгоритме матрица накопленных затрат Q и матрица направлений C интерпретируются как двумерные изображения. Значение каждого элемента матрицы соответствует уровню яркости изображения. Алгоритм построения веера оптимальных траекторий реализуется как многоступенчатый пространственный параметрический ранговый фильтр минимума с маской размером 3Ѓ~3 (рис. 1).

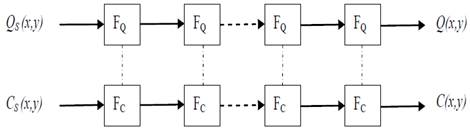
Рисунок 1 — Многоступенчатый фильтр оптимальных затрат.

Рисунок 2 — Маска пространственного фильтра Фильтрация производится над матрицами накопленных затрат Q = q (y, x) и матрицей шаговых управлений C = c (y, x). Матрица Z = z (y, x) определяет параметр фильтра для каждой точки (элемента) матриц Q и C. Веер траекторий строится от множества стартовых точек и распространяется по всем направлениям карты. Эффект пространственной фильтрации матриц эквивалентен ослаблению дуг в алгоритме Форда-Беллмана. Размещение фильтрующей маски в точке с координатами (y, x) показано на рис. 2. Число ступеней фильтра заведомо не определено, каждая ступень улучшает предыдущее решение. Матрица затрат Z содержит относительные затраты, приведенные к диапазону [0,1] (0 — минимальные затраты, 1 — максимальные затраты в пределах зоны). Непреодолимые области имеют значение Ѓ‡. Матрица может иметь необрабатываемые области, которые помечены символом NaN. Значение элемента матрицы z (y, x) используется как параметр пространственного фильтра в точке (y, x). Матрица накопленных затратQ = q (y, x) имеет размер матрицы Z и содержит следующие области:

• ? необрабатываемая область — точки помечены символом NaN. При выполнении пространственной фильтрации эти точки пропускаются и не участвуют в обработке;
• ? стартовые точки (в пределе это может быть одна точка) определяют границу, от которой распространяется волновой процесс накопления затрат. В начальном состоянии стартовые точки заполняются соответствующими значениями из матрицы затрат Z ;
• ? точки, до которых волновой фронт еще не дошел — имеют значение Ѓ‡. В процессе выполнения алгоритма значение этих точек изменяется и в конце первой ступени алгоритма содержит оценку минимальных затрат на движение от множества стартовых точек к данной точке.

Рисунок 3 — Возможные варианты шаговых управлений При пространственной фильтрации в классическом варианте маска последовательно перемещается вдоль строк и столбцов изображения, формируя новые значения яркости. Однако в данном случае на первой ступени фильтрации такая реализация оказывается неэффективной, поскольку большинство точек матрицы Q (имеющих бесконечные значения) не граничат со стартовыми точками и поэтому не изменяют свое значение, но, тем не менее, будут просматриваться сканирующей маской. Поэтому на первой ступени фильтрации маска перемещается только вдоль границы, отделяющей настоящее и прошлое движение от будущего. Вначале граница охватывает только стартовые точки, а затем, по мере построения веера оптимальных траекторий, она распространяется в виде волны по всей плоскости матрицы Q.

При движении маски вдоль границы только часть точек, покрываемых маской, может быть использована для вычисления накопленных затрат. Это означает, что в процессе вычисления шаговых управлений будут пропущены некоторые направления из-за того, что будущее движение нам пока не известно. После первой ступени фильтрации будут получены оценки накопленных затрат для всех точек матрицы Q (оценки первого приближения). При этом в матрице направлений C (y, x) все элементы будут содержать направления маршрута первого приближения. Последующие ступени фильтрации позволяют уточнить первое приближение.

Поскольку после первой ступени матрицы Q и C полностью определены, то на последующих ступенях фильтрации сканирование маской выполняется последовательно по строкам и столбцам, при этом фильтр маски использует все восемь возможных шаговых управлений.