Синтез системы частотным методом

В данном разделе необходимо синтезировать систему, согласованную по частотному спектру с сигналом внешнего воздействия. Синтез системы будет производиться спектральным методом.

В разделе 2 была найдена спектральная функция треугольного импульса (2.1).

.

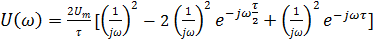
Из курса теоретической радиотехники известно, что частотная передаточная функция, согласованная с сигналом по спектру системы равна.

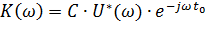
где U^*(щ) — функция комплексно сопряженная заданному спектру.

Функция, комплексно сопряженная спектральной плотности сигнала входного воздействия.

.

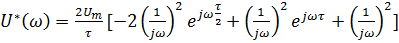
Таким образом, согласованная заданному сигналу система имеет частотную передаточную функцию.

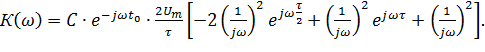
Если для упрощения предположим, что.

.

то.

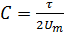
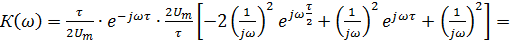
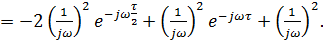
Для того, чтобы убедиться в эквивалентности синтеза согласованной системы частотным и временным методом, производится обратное преобразование Фурье по отношению к частотному коэффициенту передачи, так как импульсная характеристика связана с частотным коэффициентом передачи обратным преобразованием Фурье.

.

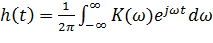
Для заданного сигнала.

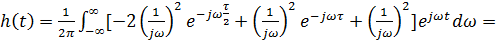
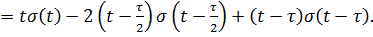
Таким образом, спектральным методом получен тот же результат, что и временным.

ОПРЕДЕЛЕНИЕ ХАРАКТЕРИСТИК СИСТЕМЫ

В данном разделе необходимо определить временные и частотные характеристики разрабатываемой системы и построить их графики. Для решения поставленной задачи будет использован пакет расширения MatLab — Control System Toolbox.

Для того, чтобы воспользоваться возможностями данного пакета необходимо перейти от частотного коэффициента передачи К (jщ) к передаточной функции К (p), которая является аналитическим продолжением К (jщ) с мнимой оси jщ на всю плоскость комплексных частот p=у+jщ.

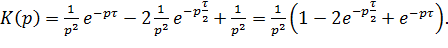
(5.1).

Учитывая параметры сигнала (см. раздел 1).

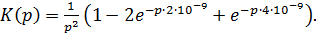
(5.2).

На основании полученной передаточной функции (5.2) рассчитываются АЧХ и ФЧХ и строятся их графики. Для этого передаточной функции (5.2) в Control System Toolbox создается TF-объект. Звено чистого запаздывания представляется передаточной функцией, полученной в результате разложения этого звена в ряд Паде (в Matlab существует встроенная процедура разложения звена чистого запаздывания в ряд Паде). Последовательность процедур для решения поставленной задачи представлена ниже. Результаты выполнения этой последовательности представлены на рисунках 5.2 — 5.9.

i=tf (1,[1 0]);

[num, den]=pade (2e-9,2);

z1=tf ([num],[den]);

[num, den]= pade (4e-9,2);

z2=tf ([num],[den]);

p=(i²)*(1−2*z1+z2);

a=pole (p).

b=zero (p).

w=0:1e+7:2e+10;

kw=j*w;

[num, den]=tfdata (p,'v');

ch=polyval (num, kw);

zn=polyval (den, kw);

ACH=abs (ch./zn);

FCH=angle (ch./zn)*180/pi;

figure (1);

plot (w, ACH,'k');

grid;

gtext ('w, rad/s');

gtext ('U, B');

figure (2);

plot (w, FCH,'k');

grid;

gtext ('w, rad/s');

gtext ('Fi, degr');

figure (3).

step (p,'k');

grid;

figure (4).

impulse (p,'k');

grid;

figure (5).

bode (p,'k');

grid;

figure (6).

nyquist (p,'k');

grid;

figure (7).

nichols (p,'k');

grid;

figure (8).

pzmap (p,'k');

grid;

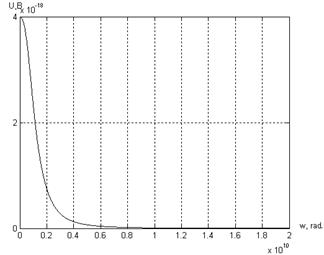
Рисунок 5.2 — График АЧХ разрабатываемой системы.

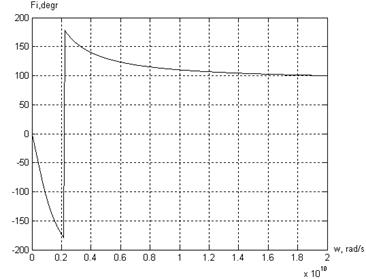
Рисунок 5.3 — График ФЧХ разрабатываемой системы.

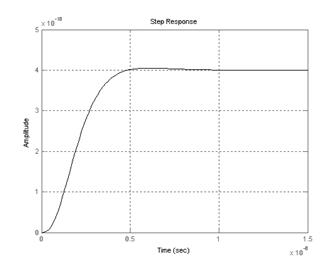
Рисунок 5.4 — График переходной характеристики разрабатываемой системы.

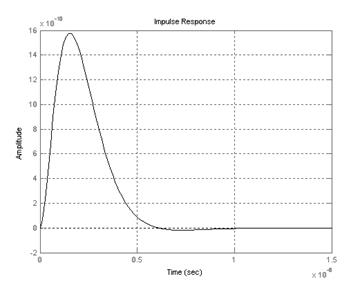
Рисунок 5.5 — График импульсной характеристики разрабатываемой системы.

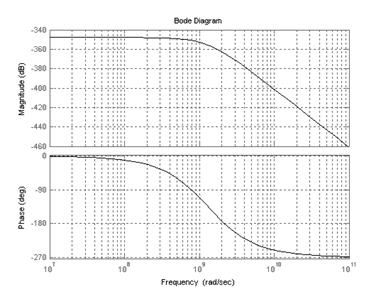
Рисунок 5.6 — Графики ЛАЧХ и ЛФЧХ разрабатываемой системы.

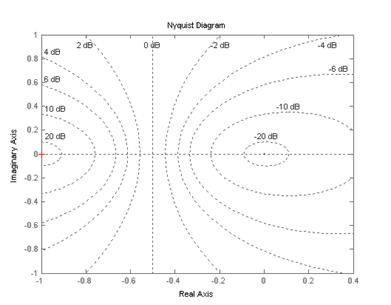
Рисунок 5.7 — График амплитудно-фазовой характеристики разрабатываемой системы.

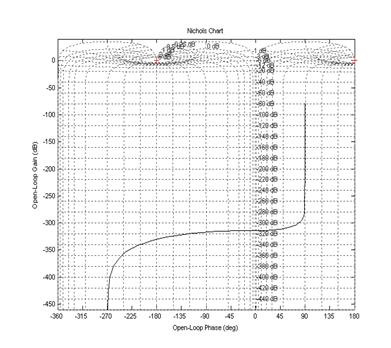
Рисунок 5.8 — График Николса разрабатываемой системы.

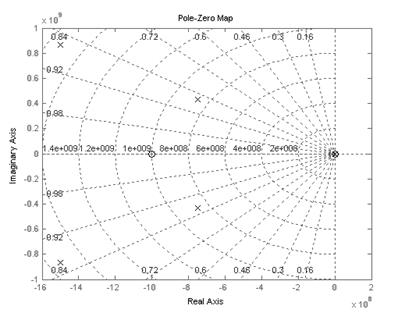
Рисунок 5.9 — Карта полюсов и нулей разрабатываемой системы.