Построение математической и компьютерной моделей решения задачи

При решении многочисленных проблем управления и планирования производства, при проектировании и перспективном планировании в разных областях практической деятельности человека возникают многовариантные задачи. Среди множества возможных способов их решения приходится отыскивать наилучшие в некотором смысле при ограничениях, налагаемых на природные, экономические, технологические и другие возможности.

В рамках современных масштабов производства неудачный выбор варианта решения может привести к значительным потерям. В связи с этим возникла необходимость применять для анализа и синтеза экономических ситуаций и систем математические методы и современную вычислительную технику. Однако непосредственное применение здесь классических методов, основанных на аппарате дифференциального исчисления, наталкивается на серьезные вычислительные трудности, что делает соответствующий аппарат неэффективным. Мощным инструментом разрешения подобного рода задач стали специальные методы поиска экстремума, составляющие содержание раздела математики, который называется математическим программированием.

Целью данной работы является сформировать ответ на теоретический вопрос «Математическое программирование. Линейная задача программирования: постановка задачи, основные методы решения», а также решить задачу экономической оптимизации, построив математическую и компьютерную модель решения задачи.

КОНТРОЛЬНЫЕ ЗАДАНИЯ

Задание № 1.

Задание: Сформировать ответ на теоретический вопрос. Математическое программирование. Линейная задача программирования: постановка задачи, основные методы решения.

Математическое программирование — раздел прикладной математики, изучающий методы поиска экстремума функций. Алгоритмы: математического программирования используются при решении оптимизационных задач, в частности, при синтезе объектов, выполняемых оптимизационными методами.

По типу целевых функций математическое программирование подразделяется на линейное математическое программирование и нелинейное математическое программирование. Иногда в отдельную группу выделяют квадратичное, выпуклое и квазивыпуклое математическое программирование.

По типу области определения целевой функции математическое программирование подразделяется на дискретное, непрерывное и дискретно-непрерывное математическое программирование. Алгоритмы непрерывного математического программирования используются при параметрическом синтезе, дискретного — для синтеза структур, дискретно-непрерывного — при структурно-параметрическом синтезе.

В зависимости от того, используются ли значения производных, а также порядка эти производных. алгоритмы математического программирования подразделяются на алгоритмы нулевого порядка (производные не используются), первого, второго и т. д. порядков (используются производные соответствующих порядков). [2].

Линейное программирование (ЛП) это область математического программирования, являющегося разделом математики и изучающего методы решения экстремальных (наибольших и наименьших) значений линейной функции конечного числа переменных, на неизвестные которой наложены линейные ограничения.

Эта линейная функция называется целевой, а ограничения, которые представляют количественные соотношения между переменными, выражающие условия и требования экономической задачи и математически записываются в виде уравнений или неравенств, называются системой ограничений.

Математическое выражение целевой функции и ее ограничений называется математической моделью экономической задачи.

В общем виде математическая модель задачи линейного программирования записывается как:

L (х)=с₁х₁ + с₂ х₂

+… + c_jх_j +… + с_пх_{п >} mах (min),.

(1)при ограничениях:

а₁₁х₁ + а₁₂х₂ +… + а_{1 j} х_j +… +а_1n х_n = b₁

а₂₁х₁ + а₂₂х₂ +… + а_{2 j} х_j +… +а_2n х_n = b₂

_…(2).

a_i1х₁ + а_i2х₂ +… + а_{i j} х_j +… +а_in х_n = b_i

_…

a_m1х₁ + а_m2х₂ +… + а_{m j} х_j +… +а_mn х_n = b_2m

х₁ ? 0; i =i.m; j= 1, n, (3).

где х₁ — неизвестные;

a_i1, b_i , c_j - заданные постоянные вели чины.

Все или некоторые уравнения системы ограничений могут быть записаны также в виде неравенств.

Для составления математической модели необходимо:

• — обозначить переменные;
• — составить целевую функцию исходя из цели задачи;
• — записать систему ограничений, учитывая имеющие в условии задачи показатели и их количественные закономерности.

Если все ограничения задачи заданы уравнениями и переменные х., неотрицательные, то модель такого вида называется канонической. Если хотя бы одно ограничение является неравенством, то модель неканоническая. Переход от неканонической формы модели к канонической осуществляется введением в каждое неравенство балансовой переменной х_п+i,. При знаке неравенства? балансовая переменная вводится в неравенство со знаком плюс, если знак неравенства? — со знаком минус. В целевую функцию балансовые переменные не вводятся.

Наиболее известными и широко применяемым на практике для решения общей задачи линейного программирования являются графический и симплекс-методы.

1 Симплекс-метод, известный также под названием метода последовательного улучшения плана, впервые разработал Г. Данциг в 1947 г. Этот метод позволяет переходить от одного допустимого базисного решения к другому, причем так, что значения целевой функции непрерывно возрастают. В результате оптимальное решение находят за конечное число шагов. Алгоритмы симплекса-метода позволяют также установить, является ли задача ЛП разрешимой. Таким образом общая идея симплексного метода (метода последовательного улучшения плана) для решения задачи линейного программирования состоит:

Задание № 2.

Для изготовления изделий, А и В используется три вида сырья. На изготовление одного изделия, А требуется 9 кг сырья первого вида, 6 кг сырья второго вида и 3 кг сырья третьего вида. На изготовление одного изделия В требуется, соответственно, 4 кг, 7 кг и 8 кг сырья. Производство «обеспечено сырьем первого вида в количестве 801 кг, второго — 807 кг, третьего — 703 кг. Прибыль от продажи изделия, А равна 3 д.е., изделия В -2 д.е. Составить план производства, максимизирующий прибыль Вначале построим математическую модель решения задачи. Обозначим: х₁ — количество произведенных изделий А, х₂ — количество произведенных изделий В. Задача оптимизации имеет вид:

• 3 х ₁ + 2х₂ > mах,
• 9 х ₁ +4х₂? 801,
• 6 х ₁ + 7х₂? 807,
• 3 х ₁ + 8х₂ ? 703,

х ₁? 0,.

х₂? 0.

В первой строке выписана целевая функция — прибыль при производстве х₁ изделий, А и х₂ изделий В. Ее требуется максимизировать, выбирая оптимальные значения переменных х₁ и х₂. При этом должны быть выполнены ограничения по ресурсу сырья (вторая, третья, четвертая строчки) — расход сырья первого вида не более 801 кг., расход сырья второго вида не более 807 кг., расход сырья третьего вида не более 703 кг. Кроме того что число произведенных изделий, А и В неотрицательны. В пятой и шестой строчках задачи и констатируется, что переменные неотрицательны.

Далее построим компьютерную модель решения задачи. На рисунке 1. представлены исходные и расчетные данные задачи.

Рисунок 1. Исходные и расчетные данные задачи.

1 В ячейки В3, В4 занесены нули в качестве первоначального приближения к решению. В дальнейшем значения этих ячеек будут подобраны автоматически.

Выделить ячейку с целевой функцией В12 и выбрать вкладку «Данные», после чего активизируем команду «Поиск решения».

Заполнить ячейки окна «Поиск решения» в соответствии с условием задачи (см. рисунок.2).

Нажать кнопку «Выполнить».

По завершении оптимизации откроется диалоговое окно «Результаты поиска решения». Установить переключатель «Сохранить найденное решение», после чего щелкните на кнопке ОК.

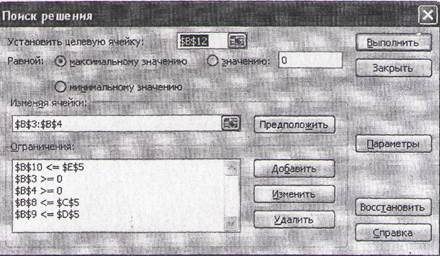
Рисунок 2. Окно «Поиск решения».

На рисунке 3 представлены результаты поиска решения.

Рисунок 3. Результаты поиска решения Ответ: чтобы максимизировать прибыль, необходимо производить 61 шт. изделий, А и 63 шт. изделий В.

математическое программирование линейная компьютерная.

ЗАКЛЮЧЕНИЕ

Содержание математического программирования составляют теория и методы решения задач о нахождении экстремумов функций на множествах, определяемых линейными и нелинейными ограничениями (равенствами и неравенствами). Математическое программирование является одним из разделов науки об исследовании операций. Задачи математического программирования находят применение в различных областях человеческой деятельности, где необходим выбор одного из возможных образов действий (программ: действий), например, при решении проблем управления и планирования производственных процессов, в проектировании и перспективном планировании, в военном деле и т. д.

Особенно широкое применение методы и модели линейного программирования получили при решении задач экономии ресурсов (выбор ресурсосберегающих технологий, составление смесей, раскрой материалов, производственно-транспортных и других задач).

Отличительной особенностью всех экономических задач, которые можно решить, применяя методы линейного программирования, является выбор вариантов решения, а также определенные ограничивающие условия. Решение подобной задачи означает выбор наиболее оптимального из всех альтернативных вариантов.