Этапы нечеткого вывода

Типовая структура процесса нечеткого вывода показана на рис. 17.

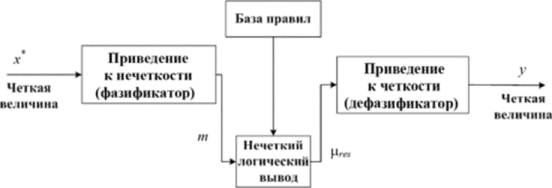
Рис, 17 — Процесс нечеткого вывода Прежде всего, должна быть сформирована база правил, представляющая собой конечное множество правил нечетких продукций. Формирование базы правил включает определение входных и выходных лингвистических переменных, а также собственно правил. Входными лингвистическими переменными называются лингвистические переменные, используемые в подусловиях правил. Выходные переменные — переменные, используемые в подзаключениях правил. Определение лингвистических переменных означает определение базовых терм-множеств переменных и функций принадлежности терм-множеств. Правила формируется, как было рассмотрено в разделе 2.4. Каждому правилу может быть приписан вес, принимающий значение из интервала [0,1]. Если вес отсутствует, можно считать, что вес равен нулю.

На вход системы нечеткого вывода поступает вектор х* =[*,*,*2,•••"?**,•••] четких значений лингвистических переменных д. Блок фаззификации (am. fuzzification — приведении к нечеткости) вычисляет степени принадлежности этих значений нечетким множествам значений лингвистических переменных. Для этого должны быть известны функции каждого терма лингвистической переменной.

Фаззификация производится следующим образом. Пусть для каждой входной лингвистической переменной д известно ее числовое значение х*. Рассматривается каждое высказывание подусловий, в котором фигурирует переменная д, например, «р. есть от «, где ос₍ -терм с известной функцией принадлежности [лАх). Значение х* используется в качестве аргумента //(л), в результате чего находится = д (х*). При этом могут использоваться модификаторы. Таким образом вычисляются значения истинности всех подусловий системы нечеткого вывода. Высказывания в подусловиях заменяются числами. На выходе блока фаззификации формируется вектор m = [//,(**),/^(х*),…//,(**),…], который является входом блока вывода.

Блок нечеткого логического вывода получает на входе вектор степени истинности всех подусловий т и вычисляет результирующую функцию принадлежности выходного значения (система вывода может иметь несколько выходов, тогда речь идет о выходном векторе). Вычисление результирующей функции принадлежности включает следующие процедуры [12] (в скобках указаны названия процедур в соответствии с международным стандартом языков программирования контроллеров IEC 1131 — Programmable Controllers. Part 7 — Fuzzy Control Programming [12]):

• — вычисление степени истинности условий (Aggregation — агрегирование);
• — определение активизированных функций принадлежности заключений (Activftion — активизация);
• — определение результирующих функций принадлежности выходных лингвистических переменных (Accumulation — аккумуляция).

В процедуре вычисления степени истинности условий по каждому из правил системы нечеткого вывода (агрегирование) рассматривается каждое условие правил системы нечеткого вывода и вычисляется степень истинности условий. Исходными данными являются степени истинности подусловий (вектор т), вычисленные в блоке фаззификации. Если условие содержит одно нечеткое высказывание вида, то степень истинности условия равна степени истинности высказывания условия. Если условие состоит из двух подусловий, связанных конъюнкцией, или дизъюнкцией, степень выполнения условия вычисляется с помощью треугольных норм (раздел 1.5). Например, для условия правила ЕСЛИ «(3, есть а,» И «Р₂ естьа₂» получаем ц (ц, дс_г')=⁷'(ц₁₁ (х;)ц"(л-;)),.

х и х₂ — значения входных переменных л;, и х₂,

Т — один из операторов t-нормы, /и_а (х) и М_а, (*) — функции принадлежности термов «, и а₂.

Аналогично для условия правила :

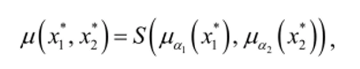
где S — один из операторов s-нормы. Если условие содержит множество подусловий, соединенных дизъюнкциями и конъюнкциями, то сначала вычисляются степени истинности подусловий, соединенных конъюнкциями, затем — дизъюнкциями. Как обычно, скобки нарушают порядок действий. Рекомендуется [12] использовать согласованные правила расчета истинности. Например, если для вычисления нечеткой конъюнкции используется операция min-пересечения, то для вычисления нечеткой дизъюнкции следует применить операцию max-объединения .

Процедура определения активизированных функций принадлежности заключений (активизация) основана на операции нечеткой импликации (раздел 2.1). Входными данными для процедуры являются степени истинности условий правил и функции принадлежности выходных величин, выходными — функции принадлежности всех подзаключений. Рассмотрим пример [14]. Пусть правило имеет вид ЕСЛИ (х= Л) ТО (у = В), функции принадлежности ц_А(х) и Мв (у) -треугольные (рис. 18), входное значение х* = 6,5, степень истинности условия /i,_f (х*) = 0,5 (см. рис. 18).

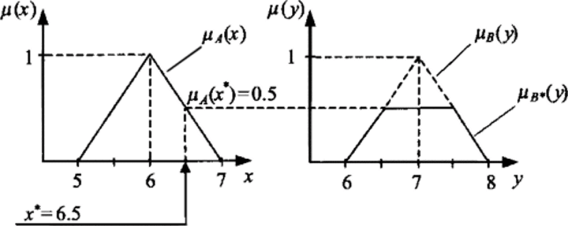
Рис. 18 — Активизация заключения с использованием импликации Мамдани Используем импликацию Мамдаии:

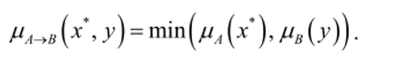
Практически активизированная функция принадлежности заключения при использовании импликации Мамдани находится простым усечением функции принадлежности заключения Мв (у) Д° уровня степень истинности условия [л_А(х*) (рис. 18). Можно использовать другие операторы нечеткой импликации.

Например, результат активизации заключения с использованием правила «произведение» показан на рис. 19.

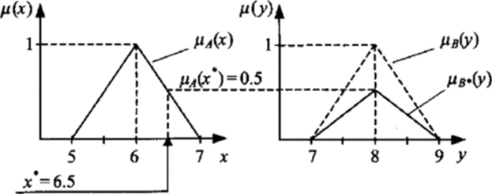
Рис. 19 — Активизация заключения с использованием правила «произведение».

На практике, особенно при наличии в правилах нескольких позаключений, удобно использовать процедуру активизации, основанную на алгоритме вывода Мамдани [12] (алгоритм будет рассмотрен в разделе 2.6). В этом алгоритме для каждого правила задастся весовой коэффициент /^е[0,1]. Может быть F/= 1, такое значение принимают, если весовой коэффициент не задан явно. Для отдельных подзаключений одного правила могут быть заданы разные весовые коэффициенты. Степень истинности всех подзаключений /-го правила рассчитывается по формуле Активизированная функция принадлежности j-го подзаключения /-го правила вычисляется по одной из формул, основанных на методе нечеткой композиции:

min-активизация /J* (д>) = min {с_п (j')};

prod-активизация //* (у) = c_t • // (у).

Рассмотренный алгоритм особенно удобен, когда правила содержат по несколько подзаключений вида .

Так как подзаключения, относящиеся к одной и той же выходной лингвистической переменной, в общем виде принадлежат разным правилам, то необходимо построить единую результирующую функцию принадлежности для каждой выходной переменной. Эта процедура называется аккумуляцией. Аккумуляция производится объединением с помощью одной из s-норм активизированных функций принадлежности каждой выходной лингвистической переменной. В результате для каждой выходной переменной получается одна функция принадлежности, возможно, весьма сложной формы.

Дефаззификация (приведение к четности) — нахождение для каждой выходной лингвистической переменной четкого значения в некотором смысле наилучшим образом, представляющим нечеткую переменную. Необходимость в дефаззификации объясняется тем, что на выходе системы нечеткого вывода нужны, как правило, четкие значения, которые поступают, например, на исполнительный механизм. Так как возможны разные критерии представления чечеткой переменной одним числом, то существуют различные методы дефаззификации [12, 14, 24]. В результате определения результирующих функций принадлежности выходных лингвистических переменных получаются результирующие функции принадлежности №res{y) — Для унимодальной функции принадлежности простейшим методом дефаззификации является выбор четкого числа, соответствующего максимальной степени принадлежности. Обобщением этого метода на многомодальные функции являются методы левого и правового модального значения.

В методе левого модального значения (LM — Lost Most Maxi mum), называемом еще метод первого максимума (FM — FirstofMaxima) [14], или наименьший из максимумов (SOM — Smallest Of Maximums) [24] в качестве четкого значения берется у = min {х_т}, где х_т — модальное значение результирующей функции принадлежности. Другими словами, в качестве четкой выходной переменной берется наименьшая (самая левая) мода.

В методе правого модального значения (RM — RightMostMaximum), называемом еще метод последнего максимума (LM — LastofMaxima), или метод наибольшего максимума (LOM — Largest Of Maximums) в качестве четкого значения берется у = тах{х_/и|, то есть наибольшая (самая правая) из мод. Примеры дефаззификации с использование левого и правого модальных значений представлены на рис. 20а и 206.

В методе среднего максимума (ММ — MidleofMaxima), или методе центра максимумов (MOM — MeanOfMaximums) находится среднее арифметическое элементов универсального множества, имеющих максимальные степени принадлежностей.

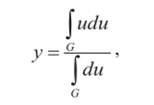
где G — множество всех элементов из интервала, имеющих максимальную степень принадлежности нечеткому множеству. Пример дефаззификации с использование метода среднего максимума представлен на рис. 20 В.

Дефаззификация по методу центра тяжести (CG — Center of Gravity, Centroid) производится по формуле определения центра тяжести плоской фигуры, ограниченной осями координат и графиком функции принадлежности нечеткого множества.

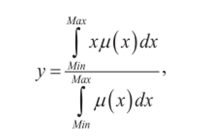
где Min и Мах — левая и правая точки интервала носителя выходной переменной.

Пример дефаззификации с использование метода центра тяжести представлен на рис. 20 В.

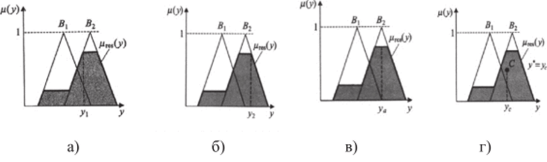
Рис. 20 — Примеры дефаззификации а) результат дефаззификации по методу левого модального значения у =у₁;

• б) результат дефаззификации по методу правого модального значения у = у₂;
• в) результат дефаззфификации по методу среднего максимума;
• г) результат дефаззификации по методу центра тяжести. Дефаззификацияпо методу центра площади (СА — Center of

Area, Bisector of Area, Bisector) состоит в нахождении такого чис;

>' Мах

ла у, что J //(x)dx= J //(x)dx. Геометрический смысл метода Мл у

состоит в нахождении такой точки на оси абсцисс, что перпендикуляр, восстановленный в этой точке, делит площадь под кривой функции принадлежности на две равные части.