Методы Адамса. 
Методика формирования и решения дифференциальных уравнений

Явные методы Адамса Итак, допустим к настоящему моменту мы вычислили значения x_i?1,…, x_i?p приближенного решения в узлах сетки t_i?1,…, t_i?p. Уравнение (1).

эквивалентно интегральному уравнению:

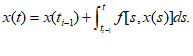
В частности, при t = t_i

Пример. Явный двухшаговый метод Адамса.

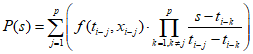
Так как метод двухшаговый, то при вычислении x_i мы используем значения x_i-1, x_i-2.

Запишем соответствующий многочлен Лагранжа:

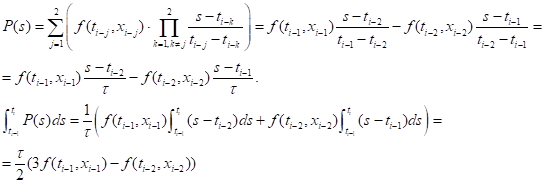
Таким образом, явный двухшаговый метод Адамса имеет вид:

Обратите внимание на следующее обстоятельство. Формула (3) неприменима при i=1: для нахождения x₁ необходимо знать x_-1.

Разумеется, (2) представляет собой лишь «заготовку» для метода. Конкретные методы получаются после вычисления коэффициентов интерполяционного полинома и интеграла.

Несомненным достоинством явных методов Адамса является тот факт, что все они независимо от своей точности требуют лишь однократного вычисления функции f (s, x (s)) на одном шаге и конкурировать с ним в этом плане весьма трудно. Остальные значения производной решения берутся из предыдущих шагов. Вместе с тем методы Адамса, как и другие многошаговые алгоритмы, не являются самостартующими, т. е. они требуют для начала интегрирования специальных стартовых алгоритмов для расчета дополнительных начальных условий.

Проблема «запуска» многошаговых методов Как уже отмечалось, существует проблема «запуска» многошаговых методов, которая связана с тем, что схема разностного метода не позволяет вычислить первые p — 1 значения. То есть, разностная схема является неполной.

Обычно эту проблемы решают так:

• — либо вычисляют первые p — 1 значение с помощью одношагового метода того же порядка точности,
• — либо вычисляют одношаговым методом более низкого порядка, но при этом используют более мелкий шаг, чтобы через соответствующее число шагов получить начальные значения с нужной точностью.

В качестве этих стартовых методов может быть использован метод Рунге-Кутты, рассматриваемый далее. Специфический способ представляют стартовые алгоритмы Ракитского, имеющие асимптотический характер. В частности, для приведенных выше методов Адамса (вплоть до четвертой степени) достаточно вычислять начальные точки по формуле:

причем уже после нескольких первых шагов обеспечивается точность, адекватная степени выбранного метода.

Неявные методы Адамса Заметим, что при выводе явных методов Адамса мы использовали значения интерполяционного полинома P на отрезке [t_i?1, t_i]. Узлы же интерполяции лежат вне и, более того, по одну сторону от этого отрезка. Известно, что в таких случаях интерполяционный полином является плохим приближением. Чтобы избежать такой ситуации, добавим к нашим узлам интерполяции узел t_i и (неизвестное) значение f (t_i, x_i), обозначив получившийся полином через Q. В результате мы получим неявный p-шаговый метод Адамса.

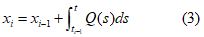
где Q — интерполяционный полином, построенный по узлам t_i?p,…, t_i и значениям f (t_i?p, x_i?p),…, f (t_i, x_i). Подчеркнем (ср. с явными и неявными методами Рунге—Кутты), что метод (4) не дает явной формулы для вычисления x_i, но представляет собой уравнение, которое должно быть разрешено относительно x_i.

Неявные метода Адамса могут быть использованы как сами по себе (тогда на каждом шаге решаются нелинейные уравнения относительно x_n+1), так и в паре с явными методами. В последнем случае значение x_n+1 сначала оценивается явным методом (х^э_n+1), а затем уточняется неявным алгоритмом. Например, такую пару образуют следующие методы:

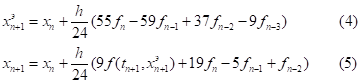
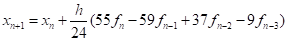
— явный метод Адамса третьей степени;

— неявный метод Адамса третьей степени.

В зарубежной литературе совместное использование явного и неявного методов называют методами прогноза — коррекции. Так же часто используют термин экстраполяционные методы для (4)и интерполяционные методы для (5).

Явные методы Адамса часто называют методами Адамса — Бэшфорта, а неявные — методами Адамса — Мултона.

Методы Рунге-Кутты Метод трапеций (6) является неявным. Если вычислить сначала по формуле (4), а затем уточнить по (6), получим одношаговый метод, называемый методом Эйлера-Коши, который является явным.

.

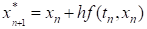
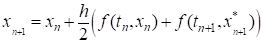
Он имеет вторую степень, которая достигается ценой двух вычислений f (t, x) на каждом шаге.

Сделаем полшага с помощью явного метода ломаных Эйлера, а затем используем полученное значение в квадратурной форме средних прямоугольников, примененной к интегралу (3). Получим метод, называемый усовершенствованным методом ломаных Эйлера.

.

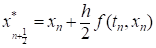
Он также имеет вторую степень и требует двукратного вычисления f (t, x) на каждом шаге.

Эти примеры укладываются в схему:

.

.

Параметры p₁, p₂, б₂, в₂ следует выбирать так, чтобы разложение (9) в ряд максимальным образом совпало с разложением точного решения (10).

,.

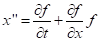
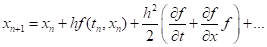
Раскладывая (9) в ряд и приравнивая коэффициенты при соответствующих степенях h, добиваемся того, что (9) задает методы второй степени.

.

, .

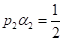
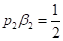
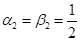
Условия (10) — три уравнения с четырьмя неизвестными, т. е. методов второй степени вида (9) оказывается бесконечно много. Если определить параметры, , получим метод Эйлера-Коши, а если, , — усовершенствованный метод ломаных Эйлера.

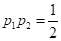
Учитывая число вычислений функций f (t, x) на одном шаге, получаем семейство методов Рунге-Кутты в виде:

,.

.

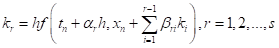
Коэффициенты методов вычисляем аналогично. При этом метод третей степени требует трех вычислений f (t, x) на каждом шаге, а метод четвертой степени — четыре. Все эти методы также образуют семейства. Среди них наиболее популярны следующие методы третьей степени:

,.

.

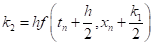
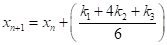
И четвертой степени:

, ,.

.

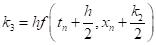
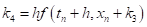
С увеличением степени метода резко возрастает число параметров p_r, б_r, в_ri и число нелинейных уравнений для их определения. С ростом степени методов трудности их построения растут по экспоненте.