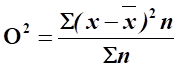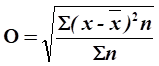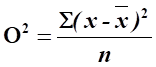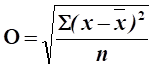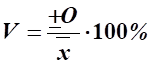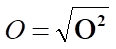Измерение величины риска (степени риска)

Величина риска (степени риска) измеряется двумя критериями: средним ожидаемым значением и колеблемостью (изменчивостью) возможного результата.

Средне ожидаемое значение — это то значение величины события, которое связано с неопределенной ситуацией; оно является средневзвешенным для всех возможных результатов, где вероятность каждого результата используется в качестве частоты или веса соответствующего значения, оно измеряет результат, который мы ожидаем в среднем.

Колеблемость возможного результата представляет собой степень отклонения ожидаемого значения от средней величины.

Для этого на практике обычно применяют два близко связанных критерия: дисперсия и средне квадратическое отклонение.

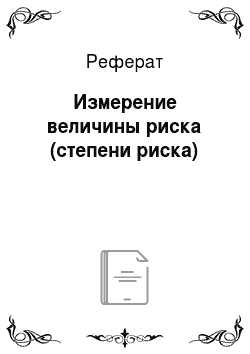
Дисперсия представляет собой среднее взвешенное из квадратов отклонений действительных результатов от средних ожидаемых:

;

где, х — ожидаемое значение для каждого случая наблюдения;

х — средне ожидаемое значение;

n — число случаев наблюдения (частота) Среднее квадратическое отклонение:

;

При равенстве частот имеет место частный случай:

; ;

Среднее квадратическое отклонение указывается в тех же единицах, в каких измеряется варьирующий признак.

Дисперсия n среднее квадратическое отклонение являются мерами абсолютной колеблемости.

Для анализа обычно используют коэффициент вариации — отношение среднего квадратического отклонения к средней арифметической и показывает степень отклонения полученных значений:

;

Коэффициент вариации — относительная величина. Поэтому на его размер не оказывает влияние абсолютные значения изучаемого показателя. С его помощью можно сравнивать даже колеблемость признаков, выраженных в разных единицах измерения.

Он изменяется от 0 до 100%.

Чем больше коэффициент, тем сильнее колеблемость; чем ниже коэффициент, тем меньше размер относительного риска.

Установлена следующая качественная оценка различных значений коэффициента вариации:

до 10% - слабая колеблемость;

10 — 25% - умеренная колеблемость;

свыше 25% - высокая колеблемость.

Существуют также несколько упрощенный метод определения степени риска.

Количественно риск инвестора характеризуется оценкой вероятной величины максимального и минимального доходов. При этом чем больше диапазон между этими величинами при равной их вероятности, тем выше степень риска. Тогда для расчета дисперсии среднего квадратического отклонения и коэффициента вариации используют следующие формулы:

О2=Рmax (хmax — х)2+Рmin (х — хmin)2;

;

;

где Рmax — вероятность получения максимального дохода (прибыли, рентабельности); хmax — максимальная величина дохода (прибыли, рентабельности); Х — среднее квадратическое отклонение.