Образование и распространение потоков волн в среде

С начала возникновения гидродинамики процессы распространения волн в среде, и образование потоков среды изучаются и исследуются относительно самостоятельно. Более того, классическая гидродинамика теоретически обосновала вывод о невозможности переноса вещества среды в потоке волн данной среды, поэтому даже прямые экспериментальные измерения оставляют в стороне вопрос о проверке или уточнении такого положения, заранее не предполагая обнаружить какие-либо потоки среды в потоках волн в данной среде.

Таким образом, согласно современным представлениям гидродинамической теории суперпозиция ударных волн в среде не вызывает образования потоков данной среды, сопровождаясь лишь передачей энергии волн без перемещения вещества в среде. За исторический период после фундаментальных трактатов Д. Бернулли «Гидродинамика» /1738 г./ и Л. Эйлера «Общие принципы движения жидкости» /1755 г./ в гидродинамике сформировалась система уравнений движения сплошной среды (жидкости или газа), которая рассматривает среду изотропной и гиротропной:

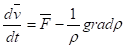
div = 0.

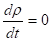
Для практических расчетов установившихся движений несжимаемой жидкости на основе уравнений широко используется первый интеграл Бернулли, частное решение которого для трубки тока можно записать:

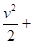
+ gh = Const.

По существу уравнение выражает собой закон сохранения энергии в трубке тока среды, что совершенно справедливо в условиях невмешательства извне в энергетический баланс данной трубки тока.

Именно поэтому, Б. Риман еще в 1860 году в своем мемуаре «О распространении плоских волн конечной амплитуды», рассматривая распространение возмущений в среде, пришел к выводу об образовании ударных волн в баротропных средах, так как:

х = tc () +().

В соответствии с выводом распространение возмущений плотности среды можно представить графически, но с учетом второго начала термодинамики волны разрежения невозможны, поэтому реально выполняется лишь правая часть графика.

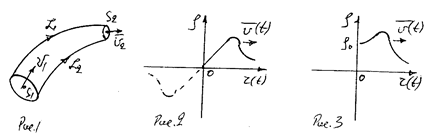
Рисунок 1.

Такие возмущения в среде называются акустическими, а описывающая их теория является линейной, не позволяя рассматривать импульсные явления с образованием в среде паро-газо-вакуумных полостей, когда жидкость уже нельзя рассматривать сплошной несжимаемой средой. Рассматривая такие импульсные явления в среде с позиций газовой динамики, на основе законов сохранения массы, импульса и энергии, мы придем к известным соотношениям Ренкина-Гюгонио, которые для плоского случая в неподвижной системе координат могут быть представлены:

₁ (D — U ₁) = ₂ (D — U₂).

P₁ +₁U₁(D — U ₁) = P ₂ + ₂ U ₂ (D — U ₂).

e₁ — e ₂ = (P₁+P ₂) (-).

где: D — скорость ударной волны, U — скорость среды,, P, e — соответственно плотность, давление и удельная внутренняя энергия жидкости. Здесь индексами 1 и 2 обозначены соответственно состояния среды по обе стороны поверхности разрыва.

В частном случае для покоящейся перед ударной волной среды, когда U₁ = 0 имеем следствия:

₁D = ₂(D — U₂).

P₁ = P₂ + ₂ U₂ (D — U₂).

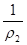
e₁ — e₂ = (P₁ + P₂) (-).

Отсюда следует вывод о том, что при условии образования ударной волны, то есть когда D 0, то имеет место U₂ 0.

Таким образом, импульсная ударная волна порождает движение сплошной среды во все стороны, то есть взрыв, который может быть направлен, например, неоднородностью среды или специальными техническими приспособлениями (отражателями, экранами и т. п.).