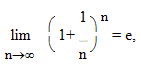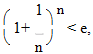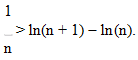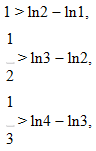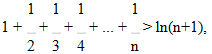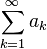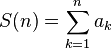Докажем расходимость гармонического ряда

Если.

где подпредельная функция монотонно возрастает, то.

где e=2.718… Возьмем от обеих частей неравенства натуральный логарифм:

или.

При n = 1,2,3, … n последовательно получим.

После сложения членов левой части неравенств получим.

или.

Если количество членов ряда неограниченно растет, то неравенство показывает, что сумма гармонического ряда неограниченно растет, т. е.

Критерий сходимости для положительных рядов

Доказать. Положительный ряд сходится тогда и только тогда, когда последовательность его частичных сумм ограничена сверху.

Доказательство:

Необходимое условие Так как ряд сходится, то последовательность частичных сумм имеет предел. Следовательно она ограничена. А значит она ограничена и снизу и сверху. Доказано Достаточное условие Дан положительный ряд и последовательность частичных сумм ограничена сверху. Покажем, что наша последовательность (из членов ряда частичных сумм) неубывающая:

Теперь используем свойство из теоремы о монотонной последовательности и получим, что последовательность частичных сумм сходится (она монотонно не убывает и ограничена сверху), следовательно ряд сходится (по определению).