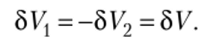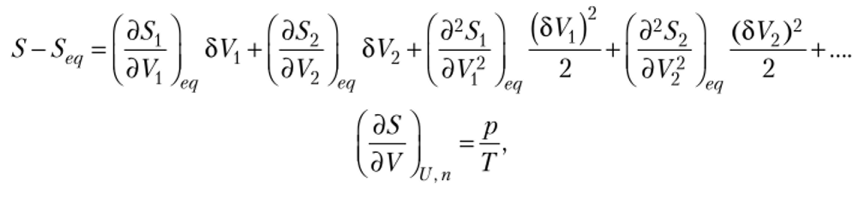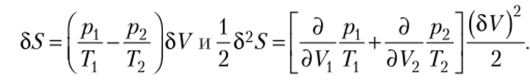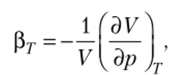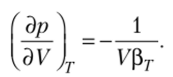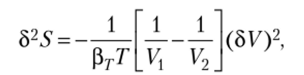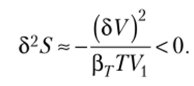Механическая устойчивость. 
Термодинамика. 
Часть 2

Рассмотрим вопрос об устойчивости системы к флуктуациям объема подсистемы при остающемся неизменным количестве вещества в ней.

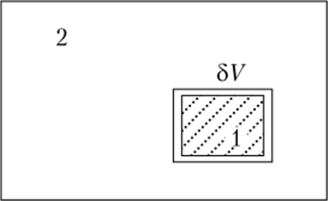
Рис. 15.4. Флуктуация объема термодинамической системы.

Как и в предыдущем случае, рассмотрим систему, разделенную на две части (рис. 15.4). Однако теперь предположим, что в частях 1 и 2 происходят малые изменения объемов 8Vj и bV₂. Поскольку объем системы по условию не меняется, то.

Рассуждая, как и прежде, разложим энтропию в ряд Тейлора относительно равновесного состояния: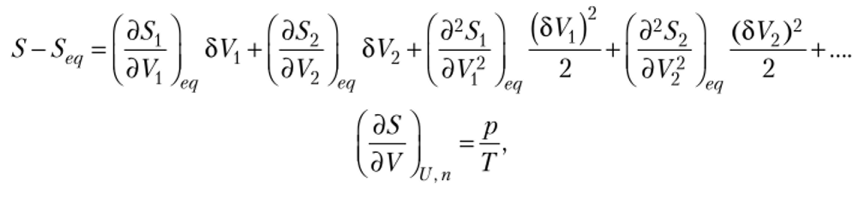

поэтому.

U Р Р2 Р о с, А В состоянии равновесия — = —^- = —, поэтому 65 =0.

М i₂ i.

Вспомним, что коэффициент изотермической сжимаемости.

откуда Положим, что 1] = 7'₂ = Г, тогда.

Очевидно, что это соотношение справедливо, если коэффициент изотермической сжимаемости положителен, (3₇ >0. В противном случае, (З_г <0, система находится в неустойчивом состоянии.

Принцип Ле Шателье — Брауна.

С условиями стабильности тесно связано положение, которое часто называют принципом наименьшего принуждения или принципом Ле Шателье — Брауна. Этот принцип в свое время был предложен А. Ле Шателье (1884 г.) и К. Брауном (1887 г.).

Простейшая формулировка принципа выглядит так: система, находящаяся в равновесии, реагирует на внешнее воздействие так, чтобы уменьшить это воздействие.

Например, если адиабатно сжимать газ, температура и давление возрастают, препятствуя сжатию. Если к системе подводится тепловая энергия, то система нагревается, при этом уменьшается разность температур между ней и нагревателем.

В некоторых простых случаях принцип Ле Шателье — Брауна просто эквивалентен условиям стабильности. Его часто применяют в химии для качественного объяснения тех или иных явлений и процессов. Однако иногда использование упрощенной формулировки принципа может привести к неверным выводам. В более точной формулировке фигурирует дополнительное условие: один из параметров пары возмущение — реакция должен быть интенсивным, а другой — экстенсивным (объем — давление, теплота — температура и т. д.).