Формирование баз знаний искднс

В основе интеллектуальной мониторинговой системы лежат базы знаний агентов БСС, включая распределенные БЗ агентов нижнего уровня и центральную БЗ агентов верхних уровней. Распределенные БЗ включают модели локальных динамических процессов, протекающих в контролируемых объектах, а центральная БЗ — модель глобального деформационного процесса и алгоритмы выработки диагностических решений.

Традиционно в качестве математических моделей динамических процессов выступают системы дифференциальных уравнений. Однако, проблема усложняется тем, что для рассматриваемых задач детальные сведения о моделируемых процессах либо отсутствуют вовсе, либо явно недостаточны. Единственная информация о свойствах таких процессов содержится в экспериментальных данных. Это приводит к необходимости разработки самообучающихся систем, способных воссоздавать модели контролируемых процессов на основе экспертной информации и объективных данных, поступающих в систему. Фактически, речь идет о реконструкции динамических систем, способных с известной степенью точности воспроизводить наблюдаемую динамику процессов, заданную в экспериментальных данных. Для решения проблемы авторы привлекают технологию мягких вычислений.

Каждый из агентов сети нижнего уровня в течение определенного интервала времени получает с контролируемого объекта информацию о развитии деформационного процесса в зоне расположения агента. На основе этой информации с использованием собственной БЗ агент вычисляет шейп развития динамического процесса на интервале и передает его через БСС агентам верхнего уровня в виде небольшого числа интегральных параметров, описывающих этот шейп. Агенты верхнего уровня на основе информации о развитии процесса в отдельных зонах конструкции определяют общую динамику процесса на интервале, интегрируют ее по всему контролируемого интервалу времени T и выносят диагностические решения.

Основными элементами распределенных БЗ мобильных агентов являются процедуры вычисления шейпов развития динамического процесса в зонах размещения агентов. Шейп формируется в виде нечетко-трендовых представлений процесса с использованием таких лингвистических термов как МАЛОЕ НАРАСТАНИЕ, РЕЗКОЕ СНИЖЕНИЕ и т. п. Для их вычисления на интервале используются нейросетевые модели (ИНС) На вход локальной ИНС подается последовательность чисел, характеризующих мгновенные значения деформаций по каждой из пространственных координат X, Y, Z, Эту информацию агент принимает от соответствующих сенсоров напряженности в течение интервала времени. Выходом ИНС является вектор нечетких термов, характеризующих шейп процесса на интервале, вместе со значениями соответствующих функций принадлежности.

База знаний агента верхнего уровня включает нечеткие продукционные правила и соответствующие им схемы вывода диагностических сообщений. Аргументами правил являются нечеткие термы, характеризующие локальные шейпы развития деформационных процессов полученные от агентов нижнего уровня. Нечеткие правила устанавливают причинно-временную связь между текущими и последующими состояниями процесса. Посылки правил характеризуют текущие значения фазовых координат (независимых переменных) динамической системы, представленные в виде нечетких числовых термов, а заключения правил — приращения фазовых координат во времени.

Нечеткие правила Сугено для БЗ агента верхнего уровня имеют вид:

где — нечеткие термы, характеризующие локальные тренды фазовых координат, — приращения фазовых координат, ci — числовые параметры. В качестве лингвистических значений нечетких переменных выступают такие термы, как: МАЛОЕ ПОЛОЖИТЕЛЬНОЕ, ОКОЛО НУЛЯ, БОЛЬШОЕ ОТРИЦАТЕЛЬНОЕ и т. п.

Для придания большей гибкости НДС предлагается вместо параметров ci, входящих в заключения правил, использовать нечеткие параметры, представленные в виде нечетких числовых термов, характеризующих приращения фазовых переменных.

Моделирование процесса на основе БЗ осуществляется путем реализации процедур нечетко-логического вывода в соответствии с теорией приблизительных рассуждений. В каждый из дискретных моментов времени t для всех независимых переменных системы на основании базы правил вычисляются их приращения с использованием механизма нечетко-логического вывода. Вычисленные нечеткие приращения прибавляются к текущим значениям переменных по правилам нечеткой арифметики и определяются новые значения переменных в последующий момент времени, после чего цикл моделирования повторяется.

Структура НДС, основанной на использовании стандартного механизма вывода из 4-этапов, приведена на рис. 1.

Нечеткий вывод начинается с этапа физзификации входных переменных, входящих в предусловия нечетких правил.

базы правил НДС, в результате чего вычисляются значения истинности предусловий правил.

.

Далее осуществляется вывод по каждому из правил путем распространения значения истинности посылки правила на его заключение .

В результате для каждого правила формируется заключение в виде вектора нечетких множеств.

.

характеризующих нечеткие приращения переменных. Затем заключения правил агрегируются на шкалах соответствующих переменных, в результате чего формируется вектор приращений координат в виде вектора нечетких множеств.

.

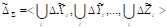
Нечеткий вывод завершается этапом дефаззификации вектора нечетких множеств путем приведения его к вектору четких значений приращений координат выходных переменных.

Рис. 1 Структура нечеткой динамической системы