Первый этап статистических исследований

Одной из задач анализа всей совокупности языков является внешнее представление их взаимосвязей, основанное на наборах признаков. Наиболее распространенным методом такого сопоставления является вычисление некоторой меры сходства или различия. Результаты сопоставления, представленные в виде матриц сходства, в свою очередь служат исходными данными для выявления структуры, образуемой языками как объектами пространства признаков. Под структурой здесь понимается в первую очередь выявление и представление близости языков и наличие градиентов — постепенных переходов от одних языков к другим в пространстве признаков, которые могут содержать важную информацию для их сопоставительного анализа.

Интересно, что использование двоичных признаков для описания языков с точки зрения возникающих при этом задач имеет сходство с исследованием видового состава растительных сообществ с использованием флористических списков. В этом случае аналогом площадки описания является язык, а аналогом списка присутствующих видов — список имеющихся у него признаков. Для каждого языка доля присутствующих признаков составляет лишь небольшую часть от всей совокупности признаков, также как и доля видов растений, встретившихся на данной площадке, составляет лишь небольшую часть от всех возможных видов. Одним из авторов подобные методы активно применялись при анализе растительных сообществ [Савельев, 2004].

Существует аналогия между языками и описаниями растительных сообществ, а так же общие проблему с вычислением мер сходства: относительно небольшое количество признаков (со значением `true') у каждого языка, разная степень информативности признаков, которая может быть обусловлена как их слишком большой распространенностью, так и уникальностью, разная степень подробности описания для различных языков, и т. д., которые создают дополнительные трудности при их сопоставлении. Кроме того, априорно неизвестно какую информацию несет каждый конкретный совпадающий признак в паре языков: информацию о непосредственном генетическом родстве этой пары, информацию о дальнем родстве (имеют общего родственника), или информацию о контактах между языками и заимствовании. Для преодоления этих трудностей были предложены различные меры сходства, в том числе ориентированные на использование именно двоичных признаков. Кроме того, для выявления и представления структуры объектов в пространстве признаков здесь разработаны и используются различные методы ординации, т. е. представления объектов в пространстве низкой размерности, обычно на плоскости.

Табл.1.

Наиболее известным способом ординации, основанным на использовании матрицы расстояний, является неметрическое многомерное шкалирование, отображающее объекты в пространство низкой размерности таким образом, что в нем Евклидовы расстояния между образами объектов пропорциональны расстояниям в исходной матрице. Это позволяет представить на плоскость «взаимоположение» объектов. Такие методы ординации основаны на вычислительных процедурах линейной алгебры, и известны достаточно давно. Кроме использования расстояний, существуют и другие методы ординации, объединяемые общим названием анализ соответствия, и позволяющие анализировать таблицы признаков с большим количеством нулей. Кроме представления структуры самих объектов, такой анализ позволяет выявлять структуру признаков и связь признаков с объектами [Legendre, 1998].

На первом этапе было отобрано 48 языков, таб.1. По техническим причинам нумерация, используемая на последующих рисунках, начата с № 2. Для них были рассчитаны расстояния, выполнена ординация и рассчитаны ошибки ординации. Все вычисления осуществлялись с помощью профессионального статистического пакета R [R, 2006], являющего, фактически, международным стандартом для проведения статистических исследований.

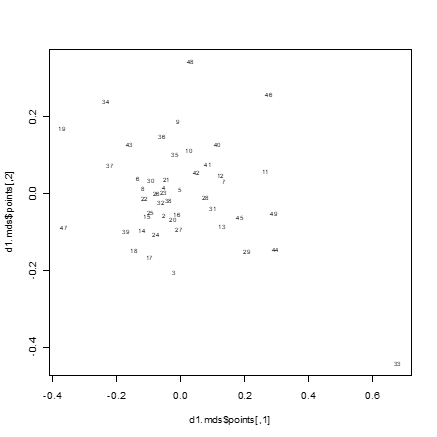
Рис. 1. Пример ординации

Для оценки качества полученной ординации, т. е. соответствия расстояний в матрице и Евклидовых расстояний на ординационной плоскости, используются как методы визуализации, так и численные характеристики. Наиболее распространенной численной характеристикой является STRESS, вычисляемая по формуле:

.

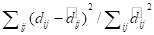
где суммирование ведется по всем парам объектов, есть исходная мера различия (расстояние) между i-м и j-м объектами (языками), а — Евклидово расстояние между i-м и j-м объектами на ординационной плоскости. Результаты вычисления STRESS для различных методов вычисления расстояния показали, что ни один из методов вычисления расстояний не дает существенно лучших результатов. В нижеследующей таблице для каждого метода слева указывается его STRESS. Рассматривались различные метрики — включенные в систему R (начиная с manhattan) и предложенные авторами статьи.

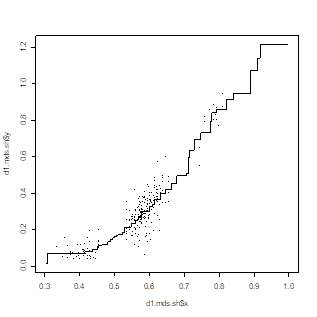
Рис. 2. График Шепарда для ординации рисунка 1

Для визуальной оценки качества ординации используется график Шепарда, в котором по горизонтали откладывается расстояние в исходноей матрице, а по вертикали — монотонная регрессия на него Евклидовых расстояний на ординационной плоскости. Если все точки лежат на ломаной, представляющей монотонную (неубывающую) регрессию, то ординаци сохранияет отношение «не больше» для расстояний: если, то и .

Табл.2.

Для содержательной оценки полученных ординаций предложен следующий подход. Языки, относящиеся к одной близкородственной группе языков (в данной выборке это славянские, германские, романские, иранские, тюркские, монгольские, уральские, северокавказские, палеоазиатские) должны располагаться на ординационной плоскости компактно. По этому критерию наилучшие результаты дает мера близости Additive-Fact-all-all. На рисунке 1 как раз и представлена ординация по этой мере.

Можно обратить внимание на следующие явно выделяющиеся данные на рис. 1. На периферии оказались следующие языки: № 19 — бирманский язык — принадлежит далеко отстоящему семейству языков (сино-тибетских), № 47 — нивхский язык — изолят, его происхождение не известно, № 46 — датский язык, как оказалось, его описание содержит ошибки (это, в частности указывает на одно из возможных применений данного метода — поиск ошибок), № 33 — русский язык оказался описан слишком подробно — «переописан».

Другим методом, совмещающим кластеризацию и ординацию, является использование непараметрических методов, относящихся к так называемым топографическим отображениям, и основанным на самоорганизации. Сюда относятся нейронные сети Кохонена (саморганизующиеся карты свойств), совмещающие классификацию методом к-средних с ординацией на плоскости [Kohonen, 1997], и генеративные топографические отображения, совмещающие нечеткую классификацию на основе Гауссовых смесей распределений с отображением классов в подпространство низкой размерности (например, на плоскость) [Bishop, 1998].

В результате применения метода нейронных сетей Кохонена с использованием всех признаков и Евклидового расстояния, был получен результат самоорганизации, представленный на рисунке 3. Для обучения использовалась нейронная сеть Кохонена SOM, топологически организованная в виде прямоугольной решетки из 7×7=49 классов. Для более полного представления о структуре классов при выводе использовалось отображение Сэммона центров классов, кроме того, вместо топологического соседства на рисунке показано минимальное остовое дерево классов. Отсутствие «перекрещиваний» в отображении Сэммона для минимального остового дерева интерпретируется как результат хорошей ординации, т. е. положения классов на ординационной плоскости соответствуют расстояниям в пространстве признаков.

Рис. 3. Кластеризация языков нейронной сетью Кохонена

Размеры классов показывают результаты калибровки полученной ординации с использованием 48 выделенных языков (калибровка осуществляется классификацией языков методом ближайшего соседа). Размер символа класса пропорционален числу отнесенных к нему языков; классы, к которым не отнесен ни один язык, показаны черными точками.

Нейронная сеть правильно объединила уральские языки (34 класс), алтайские (близкорасположенные классы 40 и 41), имеется хорошая корреляция германских языков с классом 49 и некоторые другие. В то же время ряд решений, например, помещение лезгинского языка в одну группу с германскими явно ошибочно. Требуется дальнейшая работа по настройке сети.