Суть метода. Об одной псевдоассоциативной модели текста

Представим анализируемый текст T в виде множества предложений P_i. (Название «предложение» здесь достаточно условно. На самом деле речь идет о некоторой смысловой единице — фразе в общем случае.).

T = {P_i}, i=1.N.

Каждое предложение — это упорядоченное множество лексем l_i

P_i = {lⁱ₁, lⁱ₂, …, lⁱ_k}.

Введем понятие величины псевдоассоциативной связи между лексемами l_i и l_j одного предложения. Нас интересует функционал, который определяет степень близости между лексемами на основе анализа их взаимного расположения. При этом желательно, чтобы степень близости находилась в интервале [0.1].

В простейшем случае этот функционал может быть определен так:

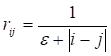
ij (1).

Параметр в знаменателе необходим для принудительного ослабления связи между соседними лексемами.

Теперь можно определить бинарные псевдоассоциации между лексемами уже на множестве предложений, т. е. на тексте. Для этого применяется следующая итерационная процедура.

• · Берется очередное предложение текста P_i.
• · Пусть на предыдущем шаге между лексемами A и B была установлена связь r'(A, B).

Если анализ P_i дает по формуле (1) между этими лексемами степень близости r''=r (A, B), то результирующее значение бинарной псевдоассоциации можно определить как.

r (A, B) = r'+r''-r'r''(2).

Это, во-первых, гарантирует сохранение итоговой оценки близости в интервале [0.1], а во-вторых — монотонно увеличивает степень связи между лексемами по мере того, как они встречаются совместно по ходу анализа предложений текста.

· Далее процесс повторяется.

Построенное таким образом множество пар бинарных псевдоассоциаций можно рассматривать как ассоциативную модель текста.

Интересно, что эта модель является работоспособной даже в самом примитивном случае, когда из текста выделяются предложения (на уровне просмотра теста до подходящего знака препинания), а лексемами объявляются последовательности символов без учета морфологии и правил словообразования.

После построения сети можно ввести слово и получить множество ассоциированных лексем. Ранжированных, например, по степени их близости. Помимо степени близости, полученной по формуле (2), можно использовать и общее количество ассоциаций для данной пары l_i, l_j (сколько раз эти лексемы встречались вместе в одном предложении) — частоту ассоциации _ij. Тогда в качестве интегральной оценки степени ассоциации можно рассматривать, скажем, произведение частоты и близости _ijr_ij.

Здесь можно вновь вернуться к формуле (1). Принудительное ослабление степени связности связано с тем, что наибольшую близость имеют лексемы, стоящие в соседних позициях. При отсутствии параметра соседние лексемы имели бы максимальную, единичную ассоциативную близость, даже если бы во всем тексте они встретились вместе лишь однажды. На самом деле, вместо функционала (1) можно было бы использовать и более тонкие функции — показательно-степенные или гиперболические, лишь бы обеспечивались их ограниченность и монотонность.

Следует отметить, что в [1] описывается несколько похожий механизм, однако в нем рассматриваются ассоциативные связи на основе частот повторения лексем в тексте. При этом каждое предложение рассматривается как вектор частот появления в нем лексем.