Информационная безопасность телекоммуникационных систем

Задание № 3

Требуется зашифровать заданное слово T₀ c помощью заданной матрицы-ключа А, а затем расшифровать зашифрованное слово.

Вид шифруемого слова и матрицы-ключа определяется номером варианта в соответствии с данными табл.3.

Таблица 3

Последняя цифра студенческого билета.
T0.	строка.	кирпич.	дерево.	кнопка.	голова.	мюзикл.	облако.	погода.	музыка.	фургон.
Предпоследняя цифра студенческого билета.
A.

Варианты матрицыключа А.

1. 2. 3. 4. 5.

Задание № 4.

Требуется выполнить шифрование и расшифрование в асимметричной криптосистеме RSA заданного сообщения при заданных значениях простыхp и q, а также открытого ключа е. Вид сообщения, значения чисел p, q и e определяются номером варианта в соответствии с данными табл.4.

Таблица 4.

Последняя цифра №студенческого билета.
p.
q.
Предпоследняя цифра № студенческого билета.
e.
Сообщение.

Вид шифруемого сообщения.

• 1. 5 764 996 751 347 924 992
• 2. 98 754 783 459 345 984
• 3. 634 923 499 192 345 216
• 4. 234 616 141 136 234 610 688
• 5. 663 487 195 324 672 768

Задание № 5.

Требуется сформировать и проверить ЭЦП Эль Гамаля при заданных начальных условиях: Р-простое целое число, G-целое число, Хсекретный ключ.

Значения P, G и X определяются номером варианта в соответствии с данными табл.5.

Таблица 5.

Последняя цифра № студенческого билета.
P.
G.
Предпоследняя цифра № студенческого билета.
X.

Задание № 6.

В симметричной криптографической системе реализовать алгоритм открытого распределения ключей Диффи-Хеллмана и вычислить общий секретный ключ K при заданных начальных условиях: Nмодуль, gпримитивный элемент, К_а и К_в -секретные ключи пользователей, А и В соответственно.

Значения N, g, К_а и К_в определяются номером варианта в соответствии с данными табл.6.

Таблица 6.

Последняя цифра №студенческого билета.
N.
g.
Предпоследняя цифра №студенческого билета.
Ka.
Kb.

Методические указания к заданию № 1.

Традиционные симметричные криптосистемы Основные понятия и определения Большинство средств защиты информации базируется на использовании криптографических шифров и процедур шифрования-расшифрования. В соответствии со стандартом ГОСТ 28 147–89 под шифром понимают совокупность обратимых преобразований множества открытых данных на множество зашифрованных данных, задаваемых ключом и алгоритмом криптографического преобразования.

Ключ-это конкретное секретное состояние некоторых параметров алгоритма криптографического преобразования данных, обеспечивающее выбор только одного варианта из всех возможных для данного алгоритма.

Основной характеристикой шифра является криптостойкость, которая определяет его стойкость к раскрытию методами криптоанализа. Обычно эта характеристика определяется интервалом времени, необходимым для раскрытия шифра.

К шифрам, используемым для криптографической защиты информации, предъявляется ряд требований:

• ? достаточная криптостойкость (надёжность закрытия данных);
• ? простота процедур шифрования и расшифрования;
• ? незначительная избыточность информации за счет шифрования;
• ? нечувствительность к небольшим ошибкам шифрования и др.

В той или иной мере этим требованиям отвечают:

• ? шифры перестановок;
• ? шифры замены;
• ? шифры гаммирования;
• ? шифры, основанные на аналитических преобразованиях шифруемых данных.

Шифрование перестановкой заключается в том, что символы шифруемого текста переставляются по определенному правилу в пределах некоторого блока этого текста. При достаточной длине блока, в пределах которого осуществляется перестановка, и сложном неповторяющемся порядке перестановки можно достигнуть приемлемой для простых практических приложений стойкости шифра.

Шифрование заменой (подстановкой) заключается в том, что символы шифруемого текста заменяются символами того же или другого алфавита в соответствии с заранее обусловленной схемой замены.

Шифрование гаммированием заключается в том, что символы шифруемого текста складываются с символами некоторой случайной последовательности, именуемой гаммой шифра. Стойкость шифрования определяется, в основном, длиной (периодом) неповторяющейся части гаммы шифра. Поскольку с помощью ЭВМ можно генерировать практически бесконечную гамму шифра, то данный способ является одним из основных для шифрования информации в автоматизированных системах.

Шифрование аналитическим преобразованием заключается в том, что шифруемый текст преобразуется по некоторому аналитическому правилу (формуле).

Например, можно использовать правило умножения вектора на матрицу, причем умножаемая матрица является ключом шифрования (поэтому ее размер и содержание должны храниться в секрете), а символами умножаемого вектора последовательно служат символы шифруемого текста. Другим примером может служить использование так называемых однонаправленных функций для построения криптосистем с открытым ключом.

Процессы шифрования и расшифрования осуществляются в рамках некоторой криптосистемы. Характерной особенностью симметричной криптосистемы является применение одного и того же секретного ключа как при шифровании, так и при расшифровании сообщений.

Шифры перестановки При шифровании перестановкой символы шифруемого текста переставляются по определенному правилу в пределах блока этого текста.

Шифрующие таблицы Правила перестановки букв в сообщении задают шифрующие таблицы. В качестве ключа в шифрующих таблицах используются:

• ? размер таблицы;
• ? слово или фраза, задающие перестановку;
• ? особенности структуры таблицы.

Одним из самых примитивных табличных шифров перестановки является простая перестановка, для которой ключом служит размер таблицы.

Задача 1.1. Зашифровать методами простой перестановки сообщение:

ТЕРМИНАТОР ПРИБЫВАЕТ СЕДЬМОГО В ПОЛНОЧЬ Решение. Сообщение записывается в таблицу поочерёдно по столбцам. Считывание производится по строкам.

Т.	Н.	П.	В.	Е.	Г.	Л.
Е.	А.	Р.	А.	Д.	О.	Н.
Р.	Т.	И.	Е.	Ь.	В.	О.
М.	О.	Б.	Т.	М.	П.	Ч.
И.	Р.	Ы.	С.	О.	О.	Ь.

Шифртекст записывается группами по пять букв:

ТНПВЕ ГЛЕАР АДОНР ТИЕЬВ ОМОБТ МПЧИР ЫСООЬ Отправитель и получатель сообщения должны заранее условиться об общем ключе в виде размера таблицы. Объединение букв шифртекста в 5-буквенные группы не входит в ключ шифра и осуществляется для удобства записи несмыслового текста. При расшифровании действия выполняют в обратном порядке.

Несколько большей стойкостью к раскрытию обладает метод шифрования, называемый одиночной перестановкой по ключу. Этот метод отличается от предыдущего тем, что столбцы таблицы переставляются по ключевому слову, фразе или набору чисел длиной в строку таблицы.

Задача 1.2.Зашифровать сообщение задачи 1.1. методом одиночной перестановки по ключу. В качестве ключа использовать слово П Е Л И К, А Н.

Решение. Составим две таблицы, заполненные текстом сообщения и ключевым словом. На рис. 1.1 представлена таблица до перестановки, а на рис. 1.2 — после перестановки.

П.	Е.	Л.	И.	К.	А.	Н.
Т.	Н.	П.	В.	Е.	Г.	Л.
Е.	А.	Р.	А.	Д.	О.	Н.
Р.	Т.	И.	Е.	Ь.	В.	О.
М.	О.	Б.	Т.	М.	П.	Ч.
И.	Р.	Ы.	С.	О.	О.	Ь.

Ключ Рис. 1.1 — Таблица до перестановки.

А.	Е.	И.	К.	Л.	Н.	П.
Г.	Н.	В.	Е.	П.	Л.	Т.
О.	А.	А.	Д.	Р.	Н.	Е.
В.	Т.	Е.	Ь.	И.	О.	Р.
П.	О.	Т.	М.	Б.	Ч.	М.
О.	Р.	С.	О.	Ы.	Ь.	И.

Рис. 1.2 — Таблица после перестановки

В верхней строке верхней таблицы записан ключ, а номера под буквами ключа определены в соответствии с естественным порядком соответствующих букв ключа в алфавите. Если бы в ключе встретились одинаковые буквы, они бы были пронумерованы слева направо. В нижней таблице столбцы переставлены в соответствии с упорядоченными номерами букв ключа.

При считывании содержимого нижней таблицы по строкам и записи шифртекста группами по пять букв получим шифрованное сообщение:

ГНВЕП ЛТООА ДРНЕР ТЕЬИО РПОТМ БЧМОР СОЫЬИ Для обеспечения дополнительной скрытности можно повторно зашифровать сообщение, которое уже прошло шифрование. Такой метод шифрования называется двойной перестановкой. В случае двойной перестановки столбцов и строк таблицы перестановки определяются отдельно для столбцов и отдельно для строк. Сначала в таблицу записывается текст сообщения, потом поочередно переставляются столбцы, а затем строки. При расшифровании порядок перестановок должен быть обратным.

Задача 1.3.Зашифровать методом двойной перестановки сообщение:

П РИ Л Е Т, А Ю В О С Ь М О Г О Для шифрования использовать ключи: по столбцам- 4 1 3 2, по строкам- 3 1 4 2.

Решение. Текст исходного сообщения записывается в таблицу 4Ч4, т.к. сообщение содержит 16 символов. Затем поочередно переставляются столбцы, а затем строки.

Исходная Перестановка Перестановка таблица столбцов строк.

	П.	Р.	И.	Л.
	Е.	Т.	А.	Ю.
	В.	О.	С.	Ь.
	М.	О.	Г.	О.
	Р.	Л.	И.	П.
	Т.	Ю.	А.	Е.
	О.	Ь.	С.	В.
	О.	О.	Г.	М.

	Т.	Ю.	А.	Е.
	О.	О.	Г.	М.
	Р.	Л.	И.	П.
	О.	Ь.	С.	В.

Если считывать шифртекст из правой таблицы построчно блоками по четыре буквы, то получится следующее:

ТЮАЕ ООГМ РЛИП ОЬСВ Число вариантов двойной перестановки быстро возрастает при увеличении размера таблицы:

• * для таблицы 3Ч3 — 36 вариантов;
• * для таблицы 4Ч4 — 576 вариантов;
• * для таблицы 5Ч5 — 14 400 вариантов.

Однако двойная перестановка не отличается высокой стойкостью и сравнительно просто «взламывается» при любом размере таблицы шифрования.

Шифрование магическими квадратами.

Магическими квадратами называют квадратные таблицы с вписанными в их клетки последовательными натуральными числами, начиная от 1, которые дают в сумме по каждому столбцу, каждой строке и каждой диагонали одно и то же число.

Шифруемый текст вписывали в магические квадраты в соответствии с нумерацией их клеток. Если затем выписать содержимое такой таблицы по строкам, то получится шифртекст, сформированный благодаря перестановке букв исходного сообщения. Считалось, что созданные с помощью магических квадратов шифртексты охраняет не только ключ, но и магическая сила.

Задача 1. 4. Зашифровать сообщение:

П Р И Л Е Т, А Ю В О С Ь М О Г О с помощью магического квадрата. Считать шифртекст построчно блоками по четыре буквы.

Решение. Используем магический квадрат 4Ч4 и заполним его заданным сообщением. Вначале пронумеруем буквы:

П Р И Л Е Т, А Ю В О С Ь М О Г О.

1 2 3 4 5 6 7 8 9 10 111 213 141 516.

О.	И.	Р.	М.
Е.	О.	С.	Ю.
В.	Т.	А.	Ь.
Л.	Г.	О.	П.

Рис. 1.3 — Магический квадрат 4×4 и его заполнение сообщением

Шифртекст, получаемый при считывании содержимого правой таблицы по строкам, имеет вид:

ОИРМ ЕОСЮ ВТАЬ ЛГОП Число магических квадратов быстро возрастает с увеличением размера квадрата. Существует только один магический квадрат размером 3×3. Количество магических квадратов 4×4 — 880, а 5×5 — 250 000.

Шифры простой замены При шифровании заменой (подстановкой) символы шифруемого текста заменяются символами того же или другого алфавита по заранее установленным правилам замены. В шифре простой замены каждый символ исходного текста заменяется символами того же алфавита одинаково на всем протяжении текста. Часто шифры простой замены называют шифрами одноалфавитной подстановки.

Шифрующие таблицы Трисемуса В 1508 г. аббат из Германии Иоганн Трисемус написал печатную работу по криптологии под названием «Полиграфия». В этой книге он впервые систематически описал применение шифрующих таблиц, заполненных алфавитом в случайном порядке. Для получения такого шифра замены обычно использовались таблица для записи букв алфавита и ключевое слово (или фраза). В таблицу сначала вписывалось по строкам ключевое слово, причем повторяющиеся буквы отбрасывались. Затем эта таблица дополнялась не вошедшими в нее буквами алфавита по порядку. При шифровании находят в этой таблице очередную букву открытого текста и записывают в шифртекст букву, расположенную ниже неё в том же столбце. Если буква текста оказывается в нижней строке таблицы, тогда для шифртекста берут самая верхнюю букву из того же столбца.

Задача 1.5. Зашифровать таблицей Трисемуса сообщение:

ВЫЛЕТАЕМ ПЯТОГО Решение. Для русского алфавита шифрующая таблица может иметь размер 48. Шифрующая таблица выглядит так:

Б.	А.	Н.	Д.	Е.	Р.	О.	Л.
Ь.	В.	Г.	Ж.	З.	И.	Й.	К.
М.	П.	С.	Т.	У.	Ф.	Х.	Ц
Ч.	Ш.	Щ.	Ы.	Ъ.	Э.	Ю.	Я.

Рис. 1.4 — Шифрующая таблица Трисемуса с ключевым словом БАНДЕРОЛЬ

Используя эту таблицу в соответствии с вышеизложенной методикой, получаем шифртекст ПДКЗЫВЗЧШЛЫЙСЙ.

Такие табличные шифры называются монограммными, так как шифрование выполняется по одной букве. Трисемус первым заметил, что шифрующие таблицы позволяют шифровать сразу по две буквы. Такие шифры называются биграммными.

Биграммный шифр Плейфейра.

Шифр Плейфейра, изобретенный в 1854 г., является наиболее известным биграммным шифром замены. Он применялся Великобританией во время первой мировой войны. Основой шифра Плейфейра является шифрующая таблица со случайно расположенными буквами алфавита исходных сообщений.

Для удобства запоминания шифрующей таблицы отправителем и получателем сообщений можно использовать ключевое слово (или фразу) при заполнении начальных строк таблицы. В целом структура шифрующей таблицы системы Плейфейра полностью аналогична структуре шифрующей таблицы Трисемуса. Поэтому для пояснения процедур шифрования и расшифрования в системе Плейфейра воспользуемся шифрующей таблицей Трисемуса из предыдущей задачи (рис. 1.4).

Процедура шифрования включает следующие шаги.

Открытый текст исходного сообщения разбивается на пары букв (биграммы). Текст должен иметь четное количество букв и в нем не должно быть биграмм, содержащих две одинаковые буквы. Если эти требования не выполнены, то текст модифицируется даже из-за незначительных орфографических ошибок.

Последовательность биграмм открытого текста преобразуется с помощью шифрующей таблицы в последовательность биграмм шифртекста по следующим правилам:

• 2а.Если обе буквы биграммы открытого текста не попадают на одну строку или столбец (как, например, буквы, А и Й в табл. на рис. 1.4), тогда находят буквы в углах прямоугольника, определяемого данной парой букв. (В нашем примере это — буквы АЙОВ. Пара букв АЙ отображается в пару ОВ. Последовательность букв в биграмме шифртекста должна быть зеркально расположенной по отношению к последовательности букв в биграмме открытого текста.)
• 2б.Если обе буквы биграммы открытого текста принадлежат одному столбцу таблицы, то буквами шифртекста считаются буквы, которые лежат под ними. (Например, биграмма НС дает биграмму шифртекста ГЩ.) Если при этом буква открытого текста находится в нижней строке, то для шифртекста берется соответствующая буква из верхней строки того же столбца. (Например, биграмма ВШ дает биграмму шифртекста ПА.)
• 2 В.Если обе буквы биграммы открытого текста принадлежат одной строке таблицы, то буквами шифртекста считаются буквы, которые лежат справа от них. (Например, биграмма, НО дает биграмму шифртекста ДЛ.) Если при этом буква открытого текста находится в крайнем правом столбце, то для шифра берут соответствующую букву из левого столбца в той же строке. (Например, биграмма ФЦ дает биграмму шифртекста ХМ.)

Задача 1.6. Зашифровать биграммным шифром Плейфера текст ВСЕ ТАЙНОЕ СТАНЕТ ЯВНЫМ Решение. Разобьём этот текст на биграммы:

ВС ЕТ АЙ, НО ЕС ТА НЕ ТЯ ВН ЫМ Данная последовательность биграмм открытого текста преобразуется с помощью шифрующей таблицы (рис. 1.5) в следующую последовательность биграмм шифртекста ГП ДУ ОВ ДЛ НУ ПД ДР ЦЫ ГА ЧТ При дешифровании применяется обратный порядок действий.

Шифрование биграммами резко повышает стойкость шифров к вскрытию. Хотя книга И. Трисемуса «Полиграфия» была относительно доступной, описанные в ней идеи получили признание лишь спустя три столетия. По всей вероятности, это было обусловлено плохой осведомленностью криптографов о работах богослова и библиофила Трисемуса в области криптографии.

Методические указания к заданию № 2.

Методы шифрования Метод перестановок на основе маршрутов Гамильтона Этот метод реализуется путем выполнения следующих шагов.

Шаг 1. Исходный текст разбивается на блоки. Если длина шифруемого текста не кратна длине блока, то на свободные места последнего блока помещаются служебные символы-заполнители (например,*).

Шаг 2. Символами блока заполняется таблица, в которой для каждого порядкового номера символа в блоке отводится вполне определенное место (рис. 2.1).

Рис. 2.1 — Вариант 8-элементной таблицы и маршрутов Гамильтона.

Шаг 3. Считывание символов из таблицы осуществляется по одному из маршрутов. Увеличение числа маршрутов повышает криптостойкость шифра. Маршруты выбирают либо последовательно, либо их очерёдность задаётся ключом К.

Шаг 4. Зашифрованная последовательность символов разбивается на блоки фиксированной длины L. Величина L может отличаться от длины блоков, на которые разбивается исходный текст на шаге 1.

Расшифрование производится в обратном порядке.

Задача 2.1. Требуется зашифровать текст <�МЕТОДЫ ПЕРЕСТАНОВКИ>. Ключ и длины зашифрованных блоков равны: К=, L=4. Для шифрования использовать таблицу и два маршрута, представленные на рис. 2.1.

Решение. Воспользуемся вышеизложенной методикой построения шифра по шагам.

Шаг 1. Исходный текст разбивается на 3 блока:

Блок =

Блок =

=.

Шаг 2. Заполняется 3 матрицы с маршрутами 2,1,1 (рис. 2.2.).

Рис. 2.2 — Шифрование с помощью маршрутов Гамильтона.

Шаг 3. Получение шифртекста путём расстановки символов в соответствии с маршрутами.

=.

Шаг4. Разбиение на блоки шифртекста.

=<ОП_Т МЕЫД ЕСРЕ ТАОН И*КВ ****>

Возможно применение и других маршрутов.

Методические указания к заданию № 3.

Аналитические методы шифрования.

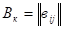
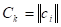
Среди аналитических методов наибольшее распространение получили методы, основанные на использовании матриц. Зашифрование К-го блока исходной информации, представленного в виде вектора осуществляется путём перемножения матрицы ключа и вектора. В результате перемножения получается блок шифртекста в виде вектора, где элементы вектора определяются по формуле:

.

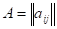
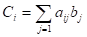
Расшифрование информации осуществляется путём последовательного перемножения векторов и обратной матрицы .

Задача 3.1. Требуется зашифровать слово = с помощью матрицы-ключа А.

A=

Решение.

1. Определим числовой эквивалент исходного слова как последовательность соответствующих порядковых номеров букв слова :

=<8,1,2,1,3,1>

• 2. Разобьём на два вектора и
• 3. Умножим матрицу А на векторы и :

=.

=.

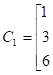
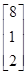
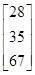
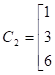
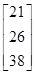
4. Зашифрованное слово запишем в виде последовательности чисел =.

Задача 3.2 Расшифровать текст, полученный в задаче 3.1.

Решение. криптосистема шифрование электронный компьютерный.

1. Вычисляется определитель .

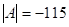
• 2. Определяется присоединённая матрица, каждый элемент которой является алгебраическим дополнением элемента матрицы А:
• 3. Получается транспонированная матрица

=.

4. Вычисляется обратная матрица по формуле:

=,.

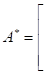
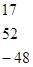
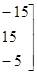
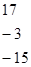
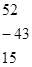
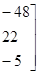
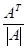
В результате вычислений обратная матрица имеет вид:

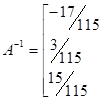
5. Определяются векторы и :

;

=.

=.

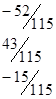
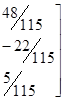
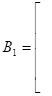
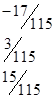
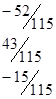
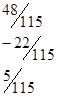
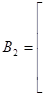
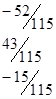
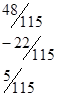
6. Получаем числовой эквивалент расшифрованного слова:

=<8,1,2,1,3,1>, который заменяется символами, в результате получается исходное слово.

Методические указания к заданию № 4.

Асимметричная криптосистема RSA.

Расширенный алгоритм Евклида.

• 1. Выбирают два больших простых числа pи q. Для большей криптостойкости p и q выбирают равной длины.
• 2. Вычисляют произведение: n=pq
• 3. Вычисляют z=(p-1)(q-1) и выбирают число е взаимно простое с z, т. е. НОД (е, z)=1.
• 4. Для вычисления закрытого (секретного) ключа d решается сравнение

еd 1modz (1).

Решение (1) имеет вид.

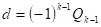
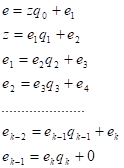
Для вычисления ключа d воспользуемся расширенным алгоритмом Евклида. Для этого число обращается в конечную цепную дробь:

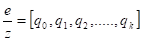
Цепная дробь имеет вид:, а последовательности и числителей и знаменателей подходящих дробей к цепной дроби определяются рекуррентно:

.

.

.

Их вычисления удобно оформить в виде таблицы:

n	— 2.	— 1.				…	k-1	k

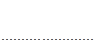
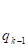
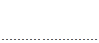
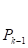
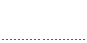
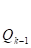
Задача 4.1.

Пусть выбраны простые числа р =47 и q=71 и открытый ключ е=79.

Требуется выполнить шифрование и дешифрование в асимметричной криптосистеме RSA сообщения.

Укажите последовательность операций.

Решение.

• 1.
• 2. Найдём секретный ключ в результате решения сравнения:

.

.

Воспользуемся расширенным алгоритмом Евклида:

• 79=3220*0+79,
• 3220=79*40+60,
• 79=60*1+19,
• 60=19*3+3,
• 19=3*6+1,
• 3=1*3+0.

Результаты вычислений сведём в таблицу:

к=5

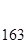
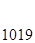
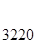
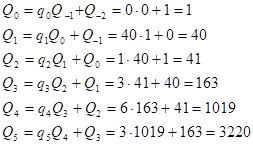
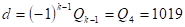
В самом деле.

.

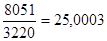
Следовательно, d=1019.

3. Разобьём сообщение на блоки mi, которые должны иметь длину, меньшую, чем п= pq = 47.17 = 3337.

, ,, ,.

4. Затем шифруем блоки:

и т. д.

Получим криптограмму: С=() =1570 2756 2091 2276 2423 0158 .

5. Для дешифрования нужно выполнить возведение в степень, используя ключ дешифрования d, т. е.

и т.д.

Методические указания к заданию № 5.

Алгоритмы электронной цифровой подписи Алгоритм цифровой подписи Эль Гамаля (EGSA).

Название EGSA происходит от слов El Gamal Signature Algorithm (алгоритм цифровой подписи Эль Гамаля). Идея EGSA основана на том, что для обоснования практической невозможности фальсификации цифровой подписи может быть использована более сложная вычислительная задача, чем разложение на множители большого целого числа, — задача дискретного логарифмирования. Кроме того, Эль Гамалю удалось избежать явной слабости алгоритма цифровой подписи RSA, связанной с возможностью подделки цифровой подписи под некоторыми сообщениями без определения секретного ключа.

Для того чтобы сгенерировать пару ключей (открытый ключ — секретный ключ), сначала выбирают некоторое большое простое целое число P и большое целое число G, причем G < P. Отправитель и получатель подписанного документа используют при вычислениях одинаковые большие целые числа P (~10³⁰⁸ или ~2¹⁰²⁴) и G (~10¹⁵⁴ или ~2⁵¹²), которые не являются секретными.

Отправитель выбирает случайное целое число X, 1< X (P -1), и вычисляет.

Y = G^X mod P.

Число Y является открытым ключом, используемым для проверки подписи отправителя. Число Y открыто передается всем потенциальным получателям документов.

Число X является секретным ключом отправителя для подписывания документов и должно храниться в секрете.

Для того чтобы подписать сообщение M, сначала отправитель хэширует его с помощью хэш-функции h (·) в целое число m:

m = h (M), 1< m < (P -1),.

и генерирует случайное целое число K, 1< K< (P -1), такое, что K и (P -1) являются взаимно простыми. Затем отправитель вычисляет целое число a:

a = G^K mod P.

и, применяя расширенный алгоритм Евклида, вычисляет с помощью секретного ключа X целое число b из уравнения.

m =(X a + K b) (mod (P -1)).

Пара чисел (a, b) образует цифровую подпись S:

S = (a, b),.

проставляемую под документом M.

Тройка чисел (M, a, b) передается получателю, в то время как пара чисел (X, K) держится в секрете.

После приема подписанного сообщения (M, a, b) получатель должен проверить, соответствует ли подпись S = (a, b) сообщению M. Для этого получатель сначала вычисляет по принятому сообщению M число.

m = h (M),.

т.е. хэширует принятое сообщение M.

Затем получатель вычисляет значение.

A = Y^a a^b (mod P).

и признает сообщение M подлинным, если, и только если.

A = G^m (mod P).

Иначе говоря, получатель проверяет справедливость соотношения.

Y^a a^b (mod P) = G^m (mod P).

Можно строго математически доказать, что последнее равенство будет выполняться тогда, и только тогда, когда подпись S=(a, b) под документом M получена с помощью именно того секретного ключа X, из которого был получен открытый ключ Y. Таким образом, можно надежно удостовериться, что отправителем сообщения M был обладатель именно данного секретного ключа X, не раскрывая при этом сам ключ, и что отправитель подписал именно этот конкретный документ M.

Выполнение каждой подписи по методу Эль Гамаля требует нового значения K, причем это значение должно выбираться случайным образом. Если нарушитель раскроет значение K, повторно используемое отправителем, то он сможет раскрыть секретный ключ X отправителя.

Задача 5.1.

Сформировать и проверить ЭЦП Эль Гамаля при следующих начальных условиях: Р=11, G=2, секретный ключ Х=8.

Решение. Вычисляем значение открытого ключа:

Y = G^X mod P = Y = 2⁸ mod 11 = 3.

Предположим, что исходному сообщению M соответствует хэш-значение m = 5.

Для того, чтобы вычислить цифровую подпись под сообщением M, имеющем хэш-значение m = 5, сначала выберем случайное целое число K = 9. Убедимся, что числа K и (P — 1) являются взаимно простыми. Действительно, НОД (9, 10) = 1.

Далее вычисляем элементы a и b подписи:

a = G^K mod P = 2⁹ mod 11 = 6,.

элемент b определяем, используя расширенный алгоритм Евклида:

m = (X a + K b) (mod (P — 1)).

При m = 5, a = 6, X = 8, K = 9, P = 11 получаем.

5 = (6 8 + 9 b)(mod 10).

или.

9 b — 43 (mod 10).

Решая сравнение, получаем b = 3. Цифровая подпись представляет собой пару: а = 6, b = 3.

Далее отправитель передает подписанное сообщение. Приняв подписанное сообщение и открытый ключ Y = 3, получатель вычисляет хэш-значение для сообщения M: m = 5, а затем вычисляет два числа:

• 1) Y^aa^b (mod P) = 3⁶ 6³ (mod 11) =10 ;
• 2) G^m (mod P) = 2⁵ (mod 11) =10.

Так как эти два целых числа равны, принятое получателем сообщение признается подлинным.

Следует отметить, что схема Эль Гамаля является характерным примером подхода, который допускает пересылку сообщения M в открытой форме вместе с присоединенным аутентификатором (a, b). В таких случаях процедура установления подлинности принятого сообщения состоит в проверке соответствия аутентификатора сообщению.

Схема цифровой подписи Эль Гамаля имеет ряд преимуществ по сравнению со схемой цифровой подписи RSA.

• 1. При заданном уровне стойкости алгоритма цифровой подписи целые числа, участвующие в вычислениях, имеют запись на 25% короче, что уменьшает сложность вычислений почти в два раза и позволяет заметно сократить объем используемой памяти.
• 2. При выборе модуля P достаточно проверить, что это число является простым и что у числа (P -1) имеется большой простой множитель (т.е. всего два достаточно просто проверяемых условия).
• 3. Процедура формирования подписи по схеме Эль Гамаля не позволяет вычислять цифровые подписи под новыми сообщениями без знания секретного ключа (как в RSA).

Однако алгоритм цифровой подписи Эль Гамаля имеет и некоторые недостатки по сравнению со схемой подписи RSA. В частности, длина цифровой подписи получается в 1,5 раза больше, что, в свою очередь, увеличивает время ее вычисления.

Методические указания к заданию № 6.

Распределение ключей в компьютерной сети При использовании для информационного обмена криптосистемы с симметричным секретным ключом два пользователя, желающие обменяться криптографически защищенной информацией, должны обладать общим секретным ключом. Пользователи должны обменяться общим ключом по каналу связи безопасным образом. Если пользователи меняют ключ достаточно часто, то доставка ключа превращается в серьезную проблему.

Для решения этой проблем можно применить два способа:

• 1) использование криптосистемы с открытым ключом для шифрования и передачи секретного ключа симметричной криптосистемы;
• 2) использование системы открытого распределения ключей Диффи-Хеллмана.

Алгоритм открытого распределения ключей Диффи-Хеллмана Алгоритм Диффи-Хеллмана был первым алгоритмом с открытыми ключами (предложен в 1976 г.). Его безопасность обусловлена трудностью вычисления дискретных логарифмов в конечном поле, в отличие от легкости дискретного возведения в степень в том же конечном поле.

Предположим, что два пользователя, А и В хотят организовать защищенный коммуникационный канал.

1. Обе стороны заранее уславливаются о модуле N (N должен быть простым числом) и примитивном элементе g, (1 g N -1).

Эти два целых числа N и g могут не храниться в секрете. Как правило, эти значения являются общими для всех пользователей системы.

• 2. Затем пользователи, А и В независимо друг от друга выбирают собственные секретные ключи k_А и k_В (k_А и k_В — случайные большие целые числа, которые хранятся пользователями, А и В в секрете).
• 3. Далее пользователь, А вычисляет открытый ключ

y_A = (mod N),.

а пользователь В — открытый ключ.

y_В = (mod N).

• 4. Затем стороны, А и В обмениваются вычисленными значениями открытых ключей y_A и y_В по незащищенному каналу.
• 5. Далее пользователи, А и В вычисляют общий секретный ключ, используя следующие выражения:

пользователь А: К = = (mod N);

пользователь В: Кґ = = (mod N).

При этом К = Кґ, так как = (mod N).

Схема реализации алгоритма Диффи-Хеллмана показана на рис. 6.1.

Задача 6.1.

Реализовать алгоритм открытого распределения ключей Диффи-Хеллмана при следующих начальных условиях: модуль N=47, примитивный элемент g=23, секретные ключи пользователей, А и В: K_А=12, К_В=33 соответственно.

Решение. Для того, чтобы иметь общий секретный ключ К, пользователи, А и В сначала вычисляют значения частных открытых ключей:

y_A = (mod N)= 23¹²(mod 47) = 27 ,.

y_В = (mod N)= 23³³(mod 47) = 33.

После того, как пользователи, А и В обменяются своими значениями y_A и y_В, они вычисляют общий секретный ключ К =(mod N)=(mod N)= 33¹²(mod 47)= 27³³ (mod 47)= =23^12*33 (mod 47)= 25 .

Кроме того, они находят секретный ключ расшифрования, решая следующее сравнение:

К К* 1 (mod N -1),.

откуда К* = 35.

Если сообщение М =16, то криптограмма:

С = М^К =16²⁵(mod 47) = 21.

Получатель восстанавливает сообщение :

М = С^К* = 21³⁵(mod 47) =16.

Злоумышленник, перехватив значения N, g, y_А и y_В, тоже хотел бы определить значение ключа К. Очевидный путь для решения этой задачи состоит в вычислении такого значения k_А по N, g, y_А, что mod N = y_А (поскольку в этом случае, вычислив k_А, можно найти К=mod N). Однако нахождение k_А по N, g и y_А — задача нахождения дискретного логарифма в конечном поле, которая считается неразрешимой.

Выбор значений N и g может иметь существенное влияние на безопасность этой системы. Модуль N должен быть большим и простым числом. Число (N -1)/2 также должно быть простым числом. Число g желательно выбирать таким, чтобы оно было примитивным элементом множества Z_N.

Алгоритм открытого распределения ключей ДиффиХеллмана позволяет обойтись без защищенного канала для передачи ключей. Однако, работая с этим алгоритмом, необходимо иметь гарантию того, что пользователь, А получил открытый ключ именно от пользователя В, и наоборот. Эта проблема решается с помощью электронной подписи, которой подписываются сообщения об открытом ключе.

Рекомендуемая литература

Основная.

1. Галатенко В. А. Основы информационной безопасности. Курс лекций. М.: Интернет-Университет Информационных технологий, 2012 г. www.intuit.ru.

Дополнительная.

• 2. Информационная безопасность открытых систем: Учебник для вузов. В 2-х томах. Том1-Угрозы, уязвимости, атаки и подходы к защите/С.В.Запечников, Н. Г. Милославская, А. И. Толстой, Д. В. Ушаков.-М.: Горячая линия-Телеком, 2006.-536 с: ил.
• 3. Информационная безопасность открытых систем: Учебник для вузов. В 2-х томах. Том2-Средства защиты в сетях/С.В.Запечников, Н. Г. Милославская, А. И. Толстой, Д. В. Ушаков.-М.: Горячая линия-Телеком, 2008.-558 с: ил.