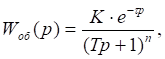Определение передаточной функции объекта

Одной из первоочередных задач при синтезе АСР является получение точной математической модели объекта управления. Часто его математическое описание получают, исходя из вида переходного процесса.

Переходная характеристика объекта управления представлена на рисунке 3.

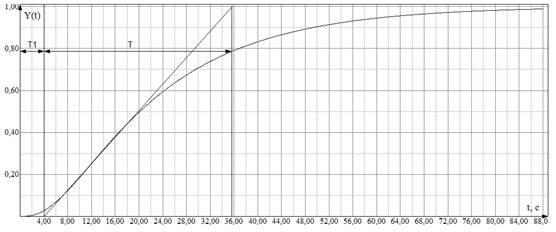
Рисунок 3. Переходная характеристика объекта управления.

Как видно из приведенного рисунка, она имеет вид переходной функции апериодического звена n-го порядка. На начальном отрезке времени выходной сигнал практически не меняет своей величины по амплитуде, т. е. отстает или опаздывает относительно входного сигнала. Поэтому в качестве передаточной функции модели объекта можно выбрать передаточную функцию следующего вида:

где К — коэффициент усиления объекта;

Т — постоянная времени;

ф (Т1) — величина запаздывания;

n — порядок объекта.

Исходя из сказанного выше, предоставляется возможность проведения процесса идентификации, который состоит из четырех этапов:

• а) экспериментальное определение переходной функции объекта управления (в данном случае — это переходная функция, представленная на рисунке 3);
• б) выбор структуры модели;
• в) определение числовых значений коэффициентов, входящих в выбранную структуру;
• г) проверка адекватности.

Процесс идентификации считается оконченным, если переходные процессы модели и объекта с необходимой точностью совпадают во всем временном диапазоне, в каждый момент времени.

В ходе процесса моделирования была получена переходная функция модели, представленная на рисунке 4.

Были получены следующие значения коэффициентов:

• — коэффициент усиления К = 1;
• — постоянная времени Т = 18;
• — величина запаздывания ф (Т1) — 8;
• — порядок объекта n — 1.

Т.к. переходные функции объекта и модели совпали во всем временном диапазоне, т. е. проверка адекватности прошла успешно, то процесс идентификации можно считать завершенным.

Передаточная функция объекта управления будет иметь вид: