Классификация цветов ириса

Знакомство с возможностями проведения дискриминантного анализа в системе Statistica 6 лучше всего начать с разбора апробированного примера. Таким примером является классический пример Фишера — анализа цветков ириса.

Задача состоит в том, чтобы по результатам измерения длины и ширины чашелистиков и лепестков цветков ириса отнести ирис к одному из трех типов: SETOSA, VERSICOL, VIRGINIC.

Данные для этого примера имеются в файле Irisdat.sta. В файле содержатся результаты измерений 150 цветков ириса, по 50 каждого типа.

Шаг 1. Нажмите кнопку Open Data (Открыть данные) и откройте файл данных Irisdat. sta из каталога Examples (Примеры на диске С). Следующий файл данных появится на экране (рисунок 1).

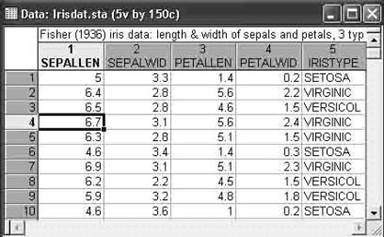
Рисунок 1 — Файл данных Iris.sta.

Шаг 2. Из Переключателя модулей Statistica откройте стартовую панель модуля Discriminate function analysis (Дискриминантный функциональный анализ) (рисунки 2, 3).

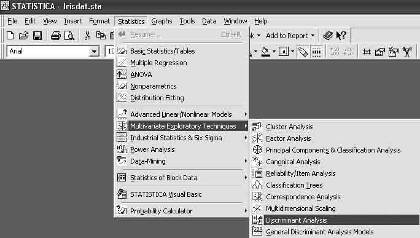
Рисунок 2 — Запуск модуля Дискриминантный анализ.

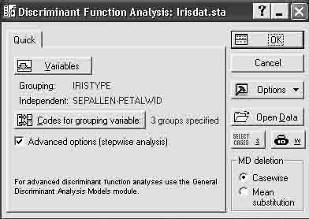
Рисунок 3 — Стартовая панель модуля Дискриминантный анализ.

Шаг 3. Сделайте установки, как показано на рисунке 3. Для этого нажмите кнопку Variables (Переменные) и выберите переменные для анализа. В качестве Grouping variable (Группирующая переменная) выберите переменную Iristype (Тип ириса) (рисунок 4).

В качестве Independent variables (Независимые переменные) выберите переменные Sepallen, Sepalwid, Petallen, Petalwid (Длина чашелистника, ширина чашелистника, длина лепестка, ширина лепестка) (рисунок 4). Нажмите кнопку ОK.

Выполните установку Codes for grouping variable (Коды для группировки переменных) (рисунок 5). Нажмите кнопку ОK.

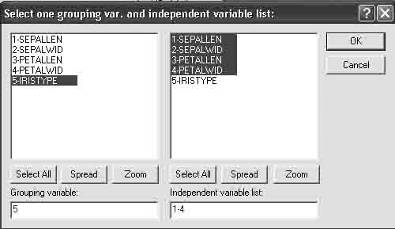
Рисунок 4 — Установка переменных (Variables).

Рисунок 5 — Установка кодов для группировки переменных.

Шаг 4. Нажмите кнопку ОK и откройте диалоговое окно Model Definition (Определение модели) (рисунок 6).

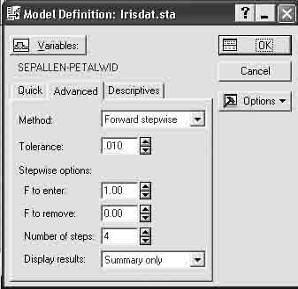
Рисунок 6 — Окно определения модели дискриминантного анализа.

Шаг 5. Сделайте установки, как показано на рисунке 6. Нажмите кнопку OK и запустите вычислительную процедуру, реализующую пошаговый метод включения.

Шаг 6. Всесторонне просмотрите итоги в диалоговом окне Discriminant Function Analysis Results (Результаты дискриминантного анализа) (рисунок 7).

Рисунок 7 — Окно результатов дискриминантного анализа данных из файла Iris. sta

Информационная часть окна сообщает, что использовано:

ь Stepwise analysis (Пошаговый анализ), Step 4 Final step (4 шага);

ь Number of variables in the model (Число переменных в модели): 4;

ь Last variable entered (Последняя включенная переменная): Sepallen, соответствующее значение статистики F-критерия (F (2, 144) = 4,72), уровень значимости р < 0,01;

ь Wilks lambda (Значение лямбды Уилкса): 0,02;

ь approx. F (4,292) = 199,14 (Приближенное значение Fстатистики), связанной с лямбдой Уилкса;

ь р — уровень значимости F-критерия для значения 199,14;

ь значения статистики лямбда Уилкса лежат в интервале 0 — 1.

Значения статистики Уилкса, лежащие около нуля, свидетельствуют о хорошей дискриминации. Значения статистики Уилкса, лежащие около единицы, свидетельствуют о плохой дискриминации.

Иными словами, это можно выразить следующим образом: если значения лямбды Уилкса близки к нулю, то мощность дискриминации (мощность = 1 — вероятность ошибки) близка к 1, если лямбда Уилкса близка к единицы, то мощность близка к нулю.

Шаг 7. Нажмите кнопку Variables in the model (Переменные, включенные в модель). На экране появится итоговая таблица анализа (рисунок 8).

дисперсия ковариация апостериорный ирис.

Рисунок 8 — Итоговая таблица анализа данных из файла Iris.sta.

Шаг 8. Просмотрите разделение групп на графике.

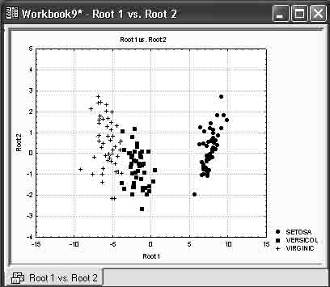
Рисунок 9 — Разделение трех типов ириса.

Для этого инициируйте кнопку Perform Canonical analysis (Канонический анализ). В появившемся диалоговом окне Canonical Analysis (канонический анализ) нажмите кнопку Scatterplot of canonical scores (Диаграмма рассеяния канонических значений). На экране появится следующий график (рисунок 9).

Шаг 9. Просмотрите функции классификации. В диалоговом окне Результаты дискриминантного анализа нажмите кнопку Classification functions (Функции классификации) (рисунок 10).

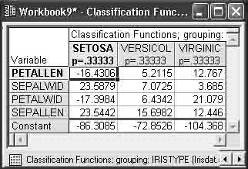
Рисунок 10 — Функции классификации, построенные пошаговым Forward stepwise (методом вперед).

С помощью этих функций можно вычислить классификационные значения (метки) для вновь наблюдаемых цветков по формулам:

SETOSA = -16,43*Sl+23,69*Sw-17,4*Pl+23,54*Pw-86,31;

VERSICOL = 5,21*Sl+7,07*Sw-6,43*Pl+15,70*Pw-72,85;

VIRGINIC = 12,76*Sl+3,69*Sw-21,08*Pl+12,5*Pw-104,37,.

где:

• — Sl — Sepallen;
• — Sw — Sepalwid;
• — Pl — Petallen;
• — Pw — Petalwid.

Пусть вы имеете новый цветок со значениями: Sepallen, Sepalwid, Petallen, Petalwid.

К какому типу ириса его отнести? Формально следует подставить эти значения в приведенные выше формулы и вычислить классификационные значения SETOSA, VERSICOL, VIRGINIC.

Новый цветок относится к тому классу, для которого классификационное значение максимально.

Конечно, построенные классификационные функции могут быть определены в электронных таблицах как формулы, и для каждого добавленного случая по ним могут быть вычислены классификационные метки. Таким образом, каждый новый объект автоматически относится к определенному классу.

Шаг 10. Нажмите кнопку Squared Mahalanobis distance (Квадрат расстояния Махаланобиса) и вы увидите таблицу с квадратами расстояния Махаланобиса от точек (случаев) до центров групп (рисунок 11).

Рисунок 11 — Расстояния Махаланобиса для данных из файла Iris. sta

Случай относится к группе, до которой расстояние Махаланобиса минимально.

Шаг 11. Апостериорные вероятности. Рассмотрите группу опций внизу диалогового окна.

Результаты дискриминантного анализа: A priori classifications probabilities (Априорные вероятности классификации). До анализа вы задаете для каждого объекта (в данном примере цветка) вероятность, с какой он принадлежит к определенному классу. После того как анализ выполнен, можно пересчитать эти вероятности и получить апостериорные вероятности классификации.

Нажав кнопку Posterior probabilities (Апостериорные вероятности), вы увидите таблицу с апостериорными вероятностями принадлежности объекта к определенному классу (рисунок 12).

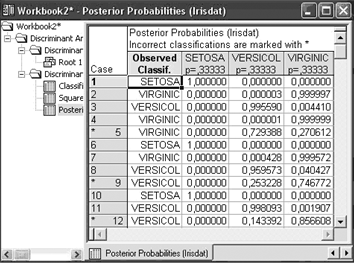
Рисунок 12 — Таблица апостериорных вероятностей.

Интерпретация данной таблицы очень проста. В первом столбце указан тип ириса для каждого случая.

Во втором, третьем, четвертом столбцах даны апостериорные вероятности отнесения каждого цветка к определенному типу.

Цветок относится к группе с максимальной апостериорной вероятностью.

Знаком * отмечаются неправильно классифицированные при использовании данного правила случаи (5, 9, 12). В исходной таблице (рисунок 1) необходимо внести изменения, а затем заново выполнить процедуру дискриминантного анализа.

Шаг 12. Классификация новых случаев. Не закрывая диалога.

Результаты дискриминантного анализа, добавьте в таблицу исходных данных новый случай (151 строка на рисунке 13).

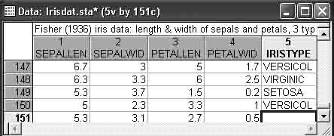
Рисунок 13 — Новое наблюдение в данных Iris.sta.

Шаг 13. Запустите процедуру дискриминантного анализа. Для того чтобы понять, к какому классу относится этот объект, нажмите кнопку Posterior probabilities (Апостериорные вероятности), вы увидите ту же таблицу с апостериорными вероятностями, к которой будет добавлена строка (рисунок 14).

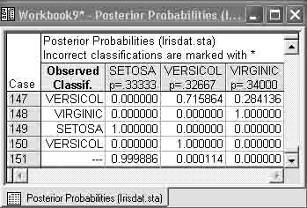
Рисунок 14 — Классификация нового наблюдения.

Итак, новое наблюдение с вероятностью 0,999 можно отнести к типу SETOSA.

Задания для выполнения

• 1. Создайте пустую электронную таблицу Spreadsheet.sta.
• 2. Внесите данные для выполнения расчетов.
• 3. Выполните процедуры дискриминантного анализа в соответствии с порядком операций, выполненных в настоящем разделе.
• 4. Дайте объяснение полученным результатам.
• 5. Из таблицы 1 внесите новые данные.
• 6. Запустите процедуру дискриминантного анализа.
• 7. Внесите поправки в исходную таблицу, пополнив обучающую выборку новой информацией.

Таблица 1 — Классификация новых случаев.