Построение модели каустики для плоскости, заданной в параметрическом виде

Построение каустик в пространстве производиться подобно двумерному случаю.

Алгоритм.

• 1. Строим геометрические фигуры, с определенными ограничениями.
• 2. Задаем плоскость, которая будет выступать в роли источника света.
• 3. Задаем точку на плоскости, из которой будет исходить луч света
• 4. Задаем направление вектора при помощи второй точки.
• 5. Через начальную точку, и направление вектора находим точку пересечения луча с плоскостью.
• 6. Строим отрезок соединяющий точку на прямой и точку пересечения.
• 7. Находим нормаль.
• 8. Строим направление отраженного от плоскости луча.
• 9. Строим прямую, определяющую направление отраженного луча.

Написание программных процедур СКМ Maple

Двумерный случай

Для начала задаем параметрическое уравнение кривой второго порядка:

r:=[t²/(2*3), t]:

Далее вводим координаты начальной точки:

x[0]: =10;

y[0]: =5;

Задаем направляющий вектор:

x_dir[0]: =-1;

y_dir[0]: =.3;

Выводим уравнение прямой, с учетом того вектор направления может быть равен нулю:

if x_dir[0]=0 then.

a:=[x[0], y_dir[0]*k+y[0]];

else.

a:=[x_dir[0]*k+x[0], y_dir[0]*k+y[0]]:

end if:

Описываем уравнение наше кривой и ограничения на которых она будет строиться:

plt[01]: =plot ([op®, t=-20.20], scaling=constrained):

Описываем точку, при помощи которой будем задавать направление луча:

plt[02]: =point ([x[0], y[0]]):

Описываем точку, которая будет задавать направления луча света выводим все значения, которые мы записали:

plt[03]: =point ([x[0]+x_dir[0], y[0]+y_dir[0]]):

Описываем уравнение нашей прямой и ограничения на которых она будет задаваться:

plt[04]: =plot ([op (a), k=-20.20], scaling=constrained):

Выводим все значения, которые мы получили (Рис. 3.4):

display ([plt[01], plt[02], plt[03], plt[04]], scaling=constrained, axes=none);

Рисунок 3.5- Построение кривой, начальной точки, и вектора направления Следующим шагом записываем систему уравнений, для нахождения точки падения луча:

tmp1:=solve (eq,{t, k});

Находим точки пересечения прямой и кривой:

y[1]: =rhs (tmp1[1][2]):

x[1]: =subs (t=rhs (tmp1[1][2]), r[1]):

y[2]: =rhs (tmp1[2][2]):

x[2]: =subs (t=rhs (tmp1[2][2]), r[1]):

Рассчитываем расстояние между корнями получившихся уравнений и начальной точкой:

per1:=sqrt ((x[1]-x[0])^2+(y[1]-y[0])^2):

per2:=sqrt ((x[2]-x[0])^2+(y[2]-y[0])^2):

Выбираем подходящую нам точку при помощи задания условия:

if evalf (sqrt ((x[1]-x[0])^2+(y[1]-y[0])^2))<(sqrt ((x[2]-x[0])^2+(y[2]-y[0])^2)) then.

x[11]: =x[1].

else x[11]: =x[2].

end if;

if evalf (sqrt ((x[1]-x[0])^2+(y[1]-y[0])^2))<(sqrt ((x[2]-x[0])^2+(y[2]-y[0])^2)) then.

y[11]: =y[1].

else y[11]: =y[2].

end if;

Для вычисления касательной находим производную:

dr:=diff (r, t);

Находим касательную:

kas:=evalf (subs (t=y[11], dr));

Задаем условие для вывода нормали и выводим нормаль:

norm1:=[kas[2],-kas[1]];

if norm1[1]*(x[0]-x[11])+norm1[2]*(y[0]-y[11])<0.

then norm1:=[-kas[2], kas[1]];

end if;

Описываем точку определяющую вектор нормали:

plt[07]: =point ([x[11]+norm1[1], y[11]+norm1[2]]):

Выводим все значения, которые мы получили (Рис. 3.5):

display ([plt[01], plt[02], plt[04], plt[07]], scaling=constrained, axes=none);

n1:=(x_dir[0]*norm1[1]+y_dir[0]*norm1[2])/(norm1[1]*norm1[1]+norm1[2]*norm1[2]):

Затем находим удвоенное произведение вектора нормали на получившуюся константу n1:

n2:=[norm1[1]*2*n1,norm1[2]*2*n1]:

Вычитаем из вектора направления вектор n2:

l:=[x_dir[0]-n2[1], y_dir[0]-n2[2]]:

Получившийся вектор l и будет вектором отражения. Запишем уравнение отражённой прямой:

lk:=solve ((x-x[11])/l[1]=(y-y[11])/l[2], y);

Описываем уравнение отраженной прямой:

plt[08]: =plot (lk, x=x[11]-5.x[11], scaling=constrained):

Выводим все значения которые мы получили (Рис. 3.6):

display ([plt[01], plt[02], plt[04], plt[05], plt[08]], scaling=constrained, axes=none);

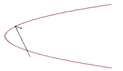
Рисунок 3.7- Построение кривой, начальной точки, и вектора направления Далее пишем процедуру для некоторого количества лучей.

Для начала зададим входные параметры: кривую в параметрическом виде и ограничения для нее:

r1:=[t²/(2*60), t]:

t1:=-10:

t2:=10:

1)Затем перейдем к первой процедуре. Первая процедура будет заполнять заданный нами массив определенными значениями. В данной процедуре будут заполняться только две точки, первая из которых является начальной, а вторая характеризует вектор направления:

prbRefLines:=proc (L, h, d1,d2,N).

global Line_, r1;

local dh, dir, i;

dir:=[d1,d2]:

dh:=(h/N):

for i from 1 to N do.

Line_[i]: =[[L,-h/2+(i-1)*dh], dir,[0,0],[0,0]];

end do:

end proc:

2)Вторая процедура будет считать точку пересечения и точку характеризующую вектор направления луча отражения:

prbRefArray:=proc (L, N).

global Line_, r1:

local dir_, x, y, a_, tmp1, kas, per1, per2,norm, l, n1,n2,k, i, dr;

# вектор направления.

for i from 1 to N do.

# расчет пересечения:

a_:=[k*Line_[i][2][1]+Line_[i][1][1], k*Line_[i][2][2]+Line_[i][1][2]]:

if Line_[i][2][1]=0 then.

a_:=x=Line_[i][1][1]:

else.

a_:=[k*Line_[i][2][1]+Line_[i][1][1], k*Line_[i][2][2]+Line_[i][1][2]]:

end if:

solve ({r1[1]=a_[1], r1[2]=a_[2]},{t, k}):

tmp1:=solve ({r1[1]=a_[1], r1[2]=a_[2]},{t, k}):

y[1]: =rhs (tmp1[1][2]):

x[1]: =subs (t=rhs (tmp1[1][2]), r1[1]):

y[2]: =rhs (tmp1[2][2]):

x[2]: =subs (t=rhs (tmp1[2][2]), r1[1]):

per1:=evalf (sqrt ((x[1]-Line_[i][1][1])^2+(y[1]-Line_[i][1][2])^2)):

per2:=evalf (sqrt ((x[2]-Line_[i][1][1])^2+(y[2]-Line_[i][1][2])^2)):

if evalf (sqrt ((x[1]-Line_[i][1][1])^2+(y[1]-Line_[i][1][2])^2)).

Line_[i][3][1]: =x[1].

else Line_[i][3][1]: =x[2].

end if:

if evalf (sqrt ((x[1]-Line_[i][1][1])^2+(y[1]-Line_[i][1][2])^2)).

Line_[i][3][2]: =y[1].

else Line_[i][3][2]: =y[2].

end if:

# Нормаль в новой точке.

dr:=diff (r1,t):

kas:=evalf (subs (t=Line_[i][3][2], dr)):

norm:=[kas[2],-kas[1]]:

if evalf (norm[1]*(Line_[i][1][1]-Line_[i][2][1])+norm[2]*(Line_[i][1][2]-Line_[i][2][2]))<0 then norm:=[-kas[2], kas[1]]:

end if:

#Вектор направления отражения.

n1:=(Line_[i][2][1]*norm[1]+Line_[i][2][2]*norm[2])/(norm[1]*norm[1]+norm[2]*norm[2]):

n2:=[norm[1]*2*n1,norm[2]*2*n1]:

l:=[Line_[i][2][1]-n2[1], Line_[i][2][2]-n2[2]]:

#точка отраженная.

Line_[i][4][1]: =l[1]:

Line_[i][4][2]: =l[2]:

end do:

end proc:

3) Третья процедура будет демонстрировать лучи падения и лучи отражения:

pprbLines:=proc (L, h, N).

global r1, t1,t2:

local pltprb, pltLines, pltLines1;

print (r1);

pltprb:=plot ([op (r1), t=t1.t2], scaling=constrained,.

color=black,.

thickness=3):

pltLines:=display (.

seq (.

line (.

Line_[i][1],.

Line_[i][3],.

color=red),.

i=1.N),.

insequence=false,.

scaling=constrained.

);

pltLines1:=display (.

seq (.

line (.

Line_[i][3],.

Line_[i][4],.

color=green),.

i=1.N),.

insequence=false,.

scaling=constrained.

);

display ([pltLines, pltprb, pltLines1], scaling=constrained, axes=none);

end proc:

И самая главная процедура которая будет включать три предыдущие и выводить наши отражения:

Mainproc:=proc (L, h, d1,d2,N).

global r1, t1,t2:

prbRefLines (L, h, d1,d2,N):

prbRefArray (L, N):

pprbLines (L, h, N):

end proc:

Mainproc (20,20,-10,-.1,10);

eval (Line_):

В результате получим следующую картинку (Рис. 3.7).

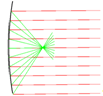
Рисунок 3.8- Каустика, при отражении лучей от параболы (параллельно падающие) Аналогично записывается написание процедур для пучка света с поправками начальные условия. Процедуру будем задавать в более удобной для нас форме. Процедура будет включать в себя три под процедуры, у каждой из которых будет своя функция (рис. 3.8).

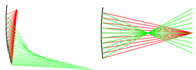
Рисунок 3.9- Каустика, при отражении лучей от параболы (пучок).

Трехмерный случай

Отражение на плоскости будем рассматривать на примере параболоида.

Задаем начальные условия для прямой:

x[0]: =0:

y[0]: =0:

z[0]: =0:

ax:=1:

ay:=-.3:

az:=10:

Задаем уравнение плоскости и уравнения прямой:

a:=x²+y²-z;

b:=x-x[0]/ax=y-y[0]/ay;

c:=y-y[0]/ay=(z-z[0])/az;

Рисуем прямую и параболоид:

pl_b:=spacecurve ([ax*t+x[0], ay*t+y[0], az*t+z[0]], t=-10.10):

pl_a:=implicitplot3d (a, x=-10.10,y=-10.10,z=-10.10,numpoints=5000):

Находим точку пересечения прямой и плоскости:

sol:=evalf (solve ({a, b, c},{x, y, z}));

x_:=evalf (subs (sol, x));

y_:=evalf (subs (sol, y));

z_:=evalf (subs (sol, z));

pl_b:=spacecurve ([ax*t+x[0], ay*t+y[0], az*t+z[0]], t=-1.1):

pl_a:=implicitplot3d (a, x=-10.10,y=-10.10,z=-10.10,numpoints=5000):

pl_c:=pointplot3d ([x_, y_, z_], color=red);

Находим производные в точках :

x1:=subs ({x=x_, y=y_, z=z_}, diff (a, x)):

y1:=subs ({x=x_, y=y_, z=z_}, diff (a, y)):

z1:=subs ({x=x_, y=y_, z=z_}, diff (a, z)):

Вектор прямой задается следующим образом:

l:=[ax, ay, az];

Вектор нормали задается следующим образом:

n1:=[x1,y1,z1]; 4.

Уравнение нормали и вывод:

pl_e:=spacecurve ([x1*t+x_, y1*t+y_, z1*t+z_], t=-8.4,color=green):

Аналогично двумерному случаю находим вектор отражения при помощи вектора падения луча и вектора нормали:

k:=dotprod (l, n1)/dotprod (n1,n1);

p:=[2*k*n1[1], 2*k*n1[2], 2*k*n1[3]];

r:=l-p;

Вектор l будет вектором отражения.

Задаем уравнение отраженного луча, и обозначаем его:

b1:=(x-x_)/r[1]=(y-y_)/r[2];

c1:=(y-y_)/r[2]=(z-z_)/r[3];

pl_d:=spacecurve ([r[1]*t+x_, r[2]*t+y_, r[3]*t+z_], t=-1.1,color=yellow):

Выводим луч падения (фиолетовый), нормаль (зеленая), отраженный луч (желтый) (Рис. 3.8).

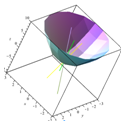
Рисунок 3.10- Отражение луча от плоскости.