Компромиссно-рентная банковская стратегия управления проблемной ссудной задолженностью юридических лиц

Одной из ключевых проблем развития российского банковского сектора продолжает оставаться высокий уровень проблемной ссудной задолженности юридических и физических лиц. В настоящее время ее доля в общем объеме кредитных вложений составляет по различным источникам от 15 до 40%. Очевидно, что существующие стратегии работы с проблемными кредитами недостаточно эффективны.

Автором предлагается компромиссно-рентная стратегия работы с проблемным должником, сущность которой заключается в следующем: формируется поток платежей предприятия-должника банку на новых условиях, отличающихся от стандартных кредитных и учитывающих доступность планируемого оттока финансовых средств из кругооборота капитала (денежных средств) фирмы, не нарушающего ее нормального функционирования. Компромиссной она именуется в виду того, что ее реализация обеспечивает интересы как банка-кредитора (предполагает компенсацию либо в полном объеме, либо некоторой части задолженности), так и предприятия-заемщика (предполагает неявную форму субсидий должнику и предоставление льготы по выплате долгов).

Рентной данную стратегию можно считать в виду того, что формирование потока положительных платежей предприятия-заемщика может быть интерпретировано как использование инструмента финансовой ренты или аннуитета, предполагающей выплаты в фиксированные (чаще всего — равные) промежутки времени. Основной отличительной особенностью потока платежей, формируемого при рассматриваемом рентном подходе (например, по сравнению с потоками выплат банку при компенсации или реструктуризации долгов) является его ориентация не на размер долговых обязательств, а на финансовые возможности предприятия, позволяющие ему осуществить эти платежи.

Для реализации данной стратегии необходимо использование трех основных параметров: размер разового платежа, частота платежей и формула-характеристика финансового потока.

Искомые параметры могут быть определены на основе теории рентных платежей. Рента характеризуется следующими параметрами:

• — член ренты (rent) — размер отдельного платежа;
• — период ренты (rent period, payment period) — временной интервал между двумя последовательными платежами;
• — срок ренты (term) — время от начала первого периода ренты до конца последнего.

На практике применяются следующие виды рент, классифицируемые по различным признакам:

• — дискретные и непрерывные (в зависимости от частоты выплат);
• — постоянные и переменные (постоянные — с одинаковыми платежами, переменные — с платежами, подчиняющимися установленному закону);
• — безусловные (подлежащие безусловной оплате) и условные (выплаты которых зависят от наступления некоторого события, например, страхового случая);
• — ограниченные по срокам (их срок заранее оговорен) и бесконечные или вечные (период взаимодействия рассматриваемых субъектов не оговорен конкретными датами);
• — немедленные или отсроченные — в зависимости от начала действия ренты;
• — постнумерандо (платежи осуществляются в конце периодов) и пренумернандо (платежи производятся в начале периодов).

Для рассматриваемой задачи может быть выбран любой подходящий к конкретной ситуации вид ренты. По мнению автора, наиболее востребованными и эффективными являются варианты рент, обладающие следующими признаками: дискретность, подчинённость размера платежей некоторой математической зависимости, обязательность платежей при ограниченности или неограниченности их сроков, привязка платежей к концу периода. При этом должны быть выполнены следующие условия:

• — значение любого рентного платежа (rent) должно быть не больше известной величины С, характеризующей предельно допустимый размер средств предприятия, подлежащих изъятию на рассматриваемом промежутке времени и определенной заранее на основе финансового анализа деятельности предприятия;
• — для случаев, предполагающих реализацию на предприятии оздоровительных инвестиционных проектов (в течение заданных проектом сроков), используется конечная рента; в противоположных случаях (когда сроки улучшения экономического состояния предприятия не определены) используется вечная рента;
• — расчетной базой для формирования рентных платежей служит ставка процента как экономический индикатор, характеризующий цену финансового ресурса, используемого предприятием-должником. При этом рентообразующим показателем может быть как кредитная (rк), так и депозитная (rд) ставка процента;
• — в случае превышения предельной величины С размера рентных платежей, рассчитанных на основе ставки процента, размер ренты может быть увеличен в целях частичного погашения долга; в противоположном случае процентная ставка, используемая для расчетов, должна быть снижена;
• — при оценке сроков погашения долга учитывается ставка дисконтирования;

Реализация компромиссно-рентной стратегии требует определения размера рентного платежа (Clim), характеризующей допустимый уровень изъятия средств у предприятия в целях возмещения банку имеющейся задолженности. Для оценки Clim могут быть использованы экономико-математические методы, ориентированные на описание деятельности предприятия. При этом среди этого комплекса методов следует выбрать динамические модели, поскольку они характеризуют достаточно долговременные последствия принятых решений (в данном случае — по размещению кредитов). С помощью таких моделей можно проследить динамику развития предприятия — возрастающая (если условия возврата кредита сформированы достаточно обосновано и происходит рост доходов) или убывающая (если погашение кредита на первых же временных интервалах подрывает инвестиционный потенциал предприятия и делает невозможными расширение производства).

К числу таких моделей относится имитационная динамическая модель предприятия, разработанная в ЦЭМИ РАН. Она позволяет осуществлять машинные (численные) эксперименты на ЭВМ для различных микроэкономических объектов. Данная модель обобщенно (в агрегированных показателях) описывает деятельность предприятия и позволяет отобразить динамику его основных экономических индикаторов (в частности, оценить выпуск и прибыль фирмы) через заданное число лет (на горизонте планирования).

Динамика развития предприятия описывается на основе рекуррентных соотношений дискретного типа, характеризующих производственный цикл. В основе модели лежит кибернетическая схема с прямыми и обратными связями, на входе которой находятся ресурсы, на выходе — выпускаемая продукция. Формулировка упрощенного варианта этой модели следующая.

Задана производственная функция типа Леонтьева (Р. Стоуна):

P= min {A/a; B/b; T/и},.

где — основные фонды (в денежном выражении); B — оборотный капитал (в денежном выражении); T — труд (в денежном выражении); a, b, и — нормативы использования соответствующих ресурсов (производственных факторов).

Задана функция затрат:

C= (a + b + и + s) P,.

где s — дополнительные (фиксированные) затраты; P — выпуск продукции в натуральном выражении.

Функция прибыли:

Mt= min {(qPt — Ct), (Qt — Ct)},.

где q — цена на продукцию; Q — спрос в денежном выражении.

Прибыль после налогообложения:

M p= M (1 — N),.

где N — ставка налогообложения.

Распределение прибыли осуществляется следующим образом:

ДA= о Mp,.

ДB= о Mp,.

ДT= о Mp,.

A'= A+ ДA,.

B'= B+ ДB,.

T'= T+ ДT,.

где 0? о1, о2, о3?1, о1+о2+о3=1 — коэффициенты распределения прибыли на прирост производственных факторов; ДA, ДB, ДT — прирост рассматриваемых производственных факторов, соответственно, A', B', T' - новые значения производственных факторов в следующем (новом) цикле производства.

Вводя к каждой из переменных модели (6 индекс t, характеризующий временной цикл производства, получим динамическую модель предприятия, развивающегося за счет своих внутренних источников. При этом соотношения (10), являющиеся собственно уравнениями динамики, могут быть переписаны следующим образом:

At+1= At+ о1Mt p.

Bt+1= Bt+ о1Mt p,.

Tt+1= Tt+ о1Mt p,.

Задавая параметры модели, можно посчитать выпуск и прибыль на любое количество временных периодов вперед.

Эту модель можно представить в виде следующей схемы (см. рис. 1).

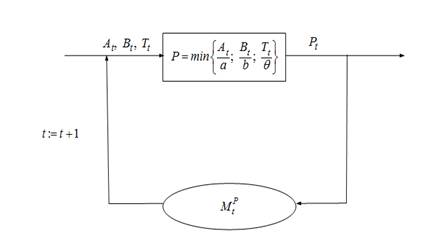
Рис. 1. Принципиальная схема имитационной модели микроэкономического объекта (предприятия)

Расчет по модели предполагает задание следующих параметров:

• 1) начальных переменных, характеризующих начальное состояние анализируемого предприятия к моменту расчета;
• 2) ряда констант (например, норм затрат производственных факторов a, b, и);
• 3) управляющих переменных: экзогенных (спрос Q и цена q) и эндогенных (коэффициентов распределения прибыли).

Данный вариант модели соответствует монопродуктовому типу производства; в случае многономенклатурного предприятия в модель встраивается блок оптимизации выбора номенклатуры выпускаемой продукции. Особенностью рассмотренного варианта модели является упрощенное представление динамики производственного процесса. Во-первых, не рассматриваются внешние финансовые источники, в частности — банковские кредиты; во-вторых, не учитывается выбытие основных фондов. Для коротких промежутков времени такое упрощение допустимо, однако в общем случае выбытие основных фондов необходимо учитывать. В связи с этим автором была модифицирована данная модель, что позволило использовать ее для рассматриваемой задачи поиска предельной величины ссудной задолженности.

Модификация модели состояла в следующем:

1. Расчетная прибыль Mp должна быть уменьшена на величину погашения долговых обязательств. Так как в поставленной авторами задаче требуется найти предельную величину выплаты долга банку (включающего в общем случае основной долг и проценты), то в этой формуле происходит вычитание Clim из Mp:

Mt pk = Mt p — Climt,.

t — период времени, .

В том случае, когда (выплата долговых обязательств одинакова по всем периодам), имеем:

Mt pk = Mt p — Clim.

При этом полагается Clim>0, то есть выполнение условия погашения долга в каждый момент t.

2. В системе равенств (10) изменяется уравнение баланса основных фондов:

At+1= (1 — rb) At +ДA,.

где rb — коэффициент выбытия основных фондов, принимается постоянным rb= const.

Заметим, что в исследуемом случае рассматривается ситуация наличия долгов перед банком безнадежных к взысканию, то есть предполагается, что кредит был выдан задолго до начала того периода, который рассматривается в модели и взаимодействие банка и должника находится в глубоком кризисе.

С учетом сказанного, система соотношений модифицированной имитационной модели предприятия имеет следующий вид.

Pt= min {At/a; Bt/b; Tt/и}.

Ct= (a + b + и + s) Pt,.

Mt= min {(qPt — Ct), (Qt — Ct)}.

Mt pk = Mt (1 — N) — Clim.

At+1= (1 — rb) At + ДAt.,.

Bt+1= Bt+ о1Mt p,.

Tt+1= Tt+ о1Mt,.

ДAt= о Mt pk,.

ДBt= о Mt pk,.

ДTt= о Mt pk,.

Используя соотношения, можно произвести серию расчетов с различным экзогенным параметром Clim. В том случае, если динамика выпуска Pt, будет возрастающей, соответствующий параметр Clim будет удовлетворять требованию доступности. Очевидно, что такие параметры в общем случае образуют некоторое множество, на котором может быть осуществлен выбор одного из них. При этом могут быть использованы критерии max Clim (при заданном темпе роста Pt), что соответствует интересам банка или же max Pt+1,/Pt, (при фиксированном уровне платежей банку в размере Clim). Таким же образом с помощью имитационных расчетов можно найти величину Clim, соответствующую нулевым темпам роста. Такая величина будет служить границей для изменения Clim.

Кроме численного подхода к определению Clim, может быть использован и аналитический подход.

С этой целью введем в модель ряд упрощений.

В новом варианте производственная функция записывается с помощью системы неравенств (что соответствует определению минимума в начальной формуле):

a Pt? At,.

b Pt? Bt,.

и Pt? Tt,.

где t — индекс временного периода (t = 1, T).

Вместо соотношения (17) можно записать:

Mt = qPt — Ct,.

Pt? Qt,.

поскольку реализованная продукция Pt не может быть больше спроса на нее Qt, где Qt — известная переменная.

Введем следующие обозначения констант:

C = a + b + и = const,.

µ = (1 — N) (q — C) = const.

Запишем уравнение динамики выпуска продукции с использованием приведенных выше соотношений:

a Pt+1? At+1 = (1 — rb) At + о1 µ Pt pk,.

b Pt+1? Bt+1 + о2 µ Pt pk,.

и Pt+1? Tt+1 + о3 µ Pt pk.

Раскроем выражение для Mt pk:

Mt pk = (1 — N) (q — c) Pt — Clim,.

Pt? Qt,.

где Clim — искомый параметр.

Оставим в правой части неравенства все известные величины, а неизвестные перенесем в левую часть и воспользуемся обозначениями:

a Pt+1 — (µ Pt — Clim) о1? (1 — rb) At,.

b Pt+1 — (µ Pt — Clim) о2? Bt,.

и Pt+1 — (µ Pt — Clim) о3? Tt,.

Pt+1? Qt+1,.

о1 + о2 + о3? 1,.

Pt+1, о1, о2, о3? 0,.

max {Pt+1}.

Соотношения описывают стандартную задачу оптимизации управления, возникающую в рамках стратегического планирования предприятий. Требуется найти такое распределение прибыли предприятия (искомые переменные о1, о2 и о3), чтобы обеспечить максимальный выпуск продукции при заданном объеме выплаты долговых обязательств (Clim).

В том случае, если считать неизвестными величинами не только о1, о2 и о3, но и Clim, то задача из линейной постановки (решаемой стандартными методами) превращается в нелинейную, решение которой производится специальными (и достаточно сложными) методами.

Однако исходная задача, которая была сформулирована в данном разделе, состояла как раз в определении Clim.

Можно показать, что задаче соответствует (при определенных условиях) обратная задача — задача банковского стратегического управления, состоящая в определении Clim. Такая задача может быть сформулирована, если известна заранее стратегия распределения прибыли предприятия (коэффициенты о1, о2 и о3). Например, ввиду ограниченности ресурсов и имеющейся системы связи с поставщиками, предприятие выделяет (в среднем) фиксированные доли прибыли (оставшейся у него в распоряжении после выплаты налогов и возврата долгов) на приобретение основных факторов производства.

Тогда задача запишется следующим образом:

a Pt+1 + о1 Clim? (1 — rb) At + о1 µ Pt,.

b Pt+1 + о2 Clim? Bt + о2 µ Pt,.

и Pt+1 + о3 Clim? Tt + о3 µ Pt,.

Pt+1? Pt,.

Pt+1? Qt+1,.

max Clim.

В задаче требуется найти max Clim с учетом 1) неубывающей динамики выпуска, 2) спроса; 3) сложившейся системы внутрипроизводственных связей и стратегий управления.

При Pt+1 = Pt получаем предельно допустимую величину Clim.

Задача еще более упрощается для частного случая — дефицитности одного из производственных факторов.

Пусть дефицитным (лимитирующим производство) фактором являются основные производственные фонды At. Это означает, что выпуск продукции непосредственно зависит от величины At:

Pt = At / a.

Используя первое неравенство системы соотношений (26), характеризующее баланс основных фондов, получаем:

At + о1 Clim? (1 — rb) At + о1 µ At.

Отсюда:

Clim? At [(1 — rb) + о1 µ - 1],.

или:

Clim? At (о1 µ - rb).

ссудный банковский проблемный имитационный Таким образом, получается условие на величину Clim. Если выбытие фондов представляет собой значительную величину, сопоставимую с их вводом в действие (µо1? rb), для нормального (растущего) воспроизводства Clim = 0.

Подводя итог сказанному выше, необходимо отметить, что предложенная стратегия не только согласует интересы предприятия и банка, но и отвечает народнохозяйственным интересам, поскольку одновременно обеспечивает сохранение предприятий, как важных хозяйствующих субъектов, и позволяет улучшать экономические результаты действующих банковских структур, что соответствует государственным целям пропорционального развития различных секторов народного хозяйства.

Кроме того, по части крупных и стратегически важных кредитов, к текущему моменту времени ставших проблемными, государство, зачастую, выступает гарантом банковских инвестиций, выражая тем самым заинтересованность в развитии кредитуемых объектов. В этих случаях описанные схемы особенно точно соответствуют концепции согласования экономических интересов участвующих агентов: предприятия пользуются (благодаря поддержке государства) привлеченными финансовыми ресурсами; государство сохраняет важные для народного хозяйства предприятия, а банки получают бессрочную ренту.