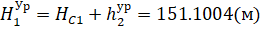Равномерное вращательное движение жесткой плиты

Принимаем гипотезу о равномерном вращательном движении жесткой плиты, на которой располагается наш локальный участок земной поверхности. При этом пункт М1 располагается на расстоянии 0,5 км от оси вращения и опускается, а пункты М2 и М3 располагаются на одной прямой, параллельной оси вращения плиты на расстоянии 0,95 км от нее.

Схему расположения мобильных пунктов на плите земной коры можно представить в следующем виде (см. рис. 2).

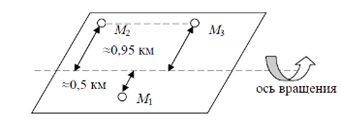
Рис. 2. Схема расположения мобильных пунктов на плите земной коры

Принимая гипотезу равномерного вращения жесткой плиты с мобильными пунктами, выполним по МНК оценивание следующих параметров: отметок мобильных пунктов и скорости вращения плиты с их точностными характеристиками; как функции указанных величин, получим оценки смещений и скоростей движений пунктов с их точностными характеристиками.

Для этого выполним следующее:

введем вектор параметров состояния объекта (локального участка земной поверхности), компонентами которого будут отметки мобильных пунктов на первую эпоху и угловая скорость вращения жесткой плиты;

получим начальную оценку (приближенные значения параметров) вектора состояния;

составим параметрические уравнения связи для измеренных превышений;

составим уравнения поправок для измеренных превышений двух эпох, для чего вычислим коэффициенты и свободные члены уравнений поправок, а также веса измеренных превышений;

решим полученные уравнения поправок по МНК;

получим оценку вектора параметров состояния объекта и средние квадратические ошибки параметров;

определим смещения и скорости движений мобильных пунктов.

При уравнивании результатов измерений параметрическим способом по МНК [2] в качестве параметров принимают такие величины, функциями которых могут быть выражены любые элементы геодезической сети (в нашем случае это могут быть отметки мобильных пунктов, непосредственно измерения — превышения, как в первую, так и во вторую эпохи, смещения мобильных пунктов, скорости смещений и т. п.). Исходя из этого, выберем в качестве параметров отметки мобильных пунктов в первую эпоху и угловую скорость вращения плиты. Тогда вектор параметров примет следующий вид:

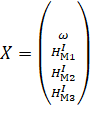
(6).

Где щ — угловая скорость вращения плиты;

— отметки мобильных пунктов в первую эпоху.

Тогда математическая модель равномерного вращательного движения жесткой плиты, на которой расположены наши мобильные пункты, может быть представлена в виде следующей системы уравнений, которые связывают отметки в первую и вторую эпохи:

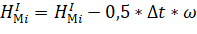
(7).

Целью уравнивания результатов измерений по МНК является исключение ошибок измерений. Для этого необходимо решить систему уравнений поправок следующего вида:

AДX + L = V (8).

Где A — матрица коэффициентов уравнений поправок, прямоугольная, число строк равно числу измерений n, а число столбцов равно числу параметров t;

Д X — вектор поправок в приближенные значения параметров;

L — вектор свободных членов уравнений поправок;

V — вектор поправок в измеренные величины.

Для составления уравнений поправок вида (8) необходимо определить матрицу коэффициентов, А и вычислить вектор L, для чего необходимо составить параметрические уравнения связи, которые связывают измеренные превышения с параметрами щ,.

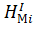
Тогда для измерений первой эпохи параметрические уравнения связи будут иметь вид:

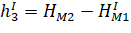
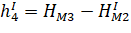
С учетом уравнений (7) параметрические уравнения связи для измерений второй эпохи будут иметь вид:

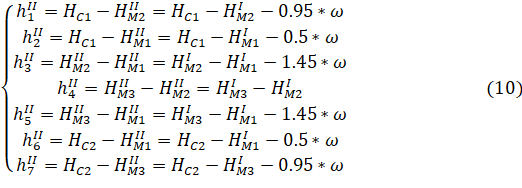
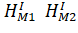
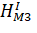
Коэффициенты уравнений поправок (элементы матрицы А) представляют собой частные производные от параметрических уравнений связи по всем параметрам (щ,) Исходя из этого получаем матрицу, А (таблицу 5).

Таблица 5 — Матрица коэффициентов уравнений поправок (А).

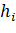	щ.
			— 1.
		— 1.
		— 1.
			— 1.
		— 1.
		— 1.
				— 1.
	— 0.95.		— 1.
	0.5.	— 1.
	1.45.	— 1.
			— 1.
	1.45.	— 1.
	0.5.	— 1.
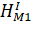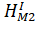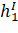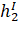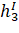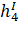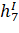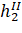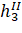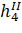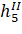	— 0.95.			— 1.

Для получения вектора свободных членов уравнений поправок L необходимо вычислить приближенные значения измеренных превышений, для чего сначала нужно получить приближенные значения вектора параметров Х и подставить их в уравнения (10) и (11).

Получим приближенные значения вектора параметров Х: для этого используем значения отметок стабильных пунктов С₁ и С₂, измеренные превышения h₁, h₂, h₇ и расстояние R от мобильного пункта М1 до оси вращения плиты и получаем:

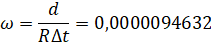
(11).

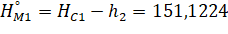
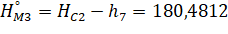
Далее определим свободные члены уравнений поправок l по формуле 12:

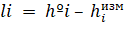
(12).

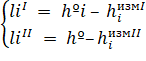
(13).

Где l — свободный член уравнения поправок для i-го измеренного превышения;

hєi — приближенное значение превышения, полученное по формулам (9), (10).

Для I эпохи приближенные значения измеренных превышений вычисляются следующим образом:

Теперь необходимо вычислить матрицу весов измеренных превышений Р.

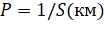
(14).

Где S_i - длина хода в км;

Р_i - вес измеренного превышения, Веса измеренных превышений имеют следующие значения:

Р1 = Р8 = 0,2381;

Р2 = Р9 = 0,3125;

Р3 = Р10 = 0,5000;

Р4 = Р11 = 0,3571;

Р5 = Р12 = 0,5000;

Р6 = Р13 = 0,3333;

Р7 = Р14 = 0,2778.

Решение полученных уравнений поправок выполняется в программе Parmo, предназначенной для решения уравнений поправок параметрическим способом по методу наименьших квадратов.

В итоге обработки программа выдает поправки в приближенные значения параметров и их средние квадратические ошибки:

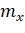0,025.	0,021.
— 0,022.	0,018.
— 0,020.	0,023.
0,013.	0,022.

СКО единицы веса Мu=0.024.

Уравненные отметки мобильных пунктов и угловой скорости находятся по формулам:

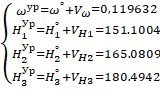
(15).

Вектор поправок в измеренные превышения и Уравненные значения превышений приведены в таблице:

№.
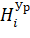	0,020.	19,9411.
	0,022.	33,9216.
	0,002.	13,9806.
	— 0,012.	15,4132.
	0,004.	29,3938.
	— 0,037.	52,6218.
	— 0,013.	23,2278.
№.
	0,089.	20,0101.
	— 0,023.	33,8766.
	0,036.	14,1517.
	— 0,007.	15,3733.
	0,026.	29,5220.
	— 0,065.	52,5346.
	0,042.	23,2828.

Контроль: