Модели и таблицы хода роста дубрав искусственного происхождения Нижнего Поволжья

Степное лесоразведение в Нижнем Поволжье существует более 100 лет. Защитные лесные насаждения, созданные здесь в середине прошлого века, представлены в основном, дубовыми древостоями искусственного происхождения, растущими в жестких почвенно-климатических условиях. Изучение закономерностей роста, состояния и развития таких лесов является актуальной задачей степного лесоразведения.

Основой исследования влияния географических и климатических условий на рост и развитие древостоев в целом является моделирование хода роста отдельных деревьев и элементов леса.

Модели и таблицы хода роста древостоев имеют большое значение для лесного хозяйства. Сведения о ходе роста и производительности насаждений служат основой для проектирования лесохозяйственных мероприятий. Существует несколько видов таблиц хода роста, подразделяемых по назначению для: нормальных насаждений, модальных насаждений, оптимальных насаждений различной густоты и разных сумм площадей сечений.

Таблицы хода роста предназначены для: характеристики и прогнозирования роста и развития древостоев; установления спелости леса и обоснования возраста рубки; проектирования лесохозяйственных мероприятий; выявления закономерностей роста и развития древостоев; составления региональных лесотаксационных нормативов.

В методологию и методику разработки таблиц хода роста и продуктивности внесли большой вклад видные ученые страны: Орлов М. М., Варгас де Бедемар, Тюрин А. В., Третьяков Н. В., Анучин H.П., Антанайтис В. В., Дракин В. Н., Вуевский Д. И., Загреев В. В., Зейде Б. Б., Кивисте А. К., Корсунь Ф. Д., Кофман Г. Б., Кузьмичев В. В., Макаренко А. А., Моисеев В. С., Моисеенко Ф. П., Мошкалев А. Г., Свалов Н. Н., Швиденко А. З. и многие другие [2, 3, 5, 6, 13].

Цель работы заключается в выборе оптимальной функции роста отдельного дерева и древостоя элемента леса для разработки таблиц хода роста различной густоты дубняков искусственного происхождения Нижнего Поволжья.

Объектом исследований послужили древостои лесных культур дуба (Quercus robur L.) в условиях степной зоны Нижнего Поволжья, которые были созданы за период с 1930 по 2010 гг.

Для выявления закономерностей хода роста деревьев и древостоев дуба использовались пробные площади, на которых работы проводились в соответствии с ОСТ-56−69−83 «Пробные площади лесоустроительные. Методы закладки» [12].

Пробные площади закладывались на участках, наиболее типичных для определения категорий таксируемых насаждений, с условием охвата возможно большего разнообразия дубрав искусственного происхождения по классу бонитета, полноте и составу.

В ходе полевых работ на территории Волгоградской, Саратовской и Самарской областей в дубравах искусственного происхождения было заложено 23 пробных площади с рубкой и обмером 131 модельного дерева (в том числе 21 модельное дерево на полный анализ хода роста). Средние таксационные показатели, характеризующие дубняки на пробных площадях приведены в таблице 1.

Таблица 1. Таксационная характеристика пробных площадей.

Рассмотрим некоторые подходы к моделированию роста и развития живых организмов.

Значительные исследования по обобщению закономерностей роста лесных насаждений провел Загреев В. В. [3], он на основании анализа 400 таблиц хода роста выявил возможность систематизации таблиц. Оказалось, что для определения хода роста сосны, например, нужна всего одна таблица с тридцатью типовыми рядами. Такие индексные таблицы служат для сравнительной оценки и группировки таблиц по степени сходства и различия в характере хода роста.

Таблицы хода роста оптимальных насаждений составили E. Assmann и F. Franz [14]. Ими было предложено в пределах каждого класса бонитета насаждения три уровня производительности (верхний, средний и низший).

Например, моделью роста в дифференциальном виде является уравнение:

.

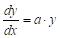
запишем его в виде:

.

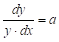
Далее интегрируя и считая, что y = b при x = 0 получим:

.

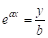
, , или .

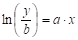
Показательная функция всегда положительная, монотонно возрастает при а> 0 и монотонно убывает при, а <0. Важным свойством этой функции является тот факт, что все её производные имеют одинаковые значения.

Митчерлих Е.А. [2, 8] при обосновании совокупного действия факторов роста при выращивании сельскохозяйственных растений рассмотрел уравнение.

.

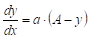
считая, что y — величина получаемого урожая, а, А — величина наивысшего урожая.

По результатам решения этого дифференциального уравнения относительно y имеем:

.

Для учета отрицательных факторов роста Митчерлих ввел «коэффициент повреждения» k и уравнение приняло следующий вид.

.

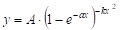
Это уравнение не получило широкого применения, но теоретические предпосылки были использованы другими исследователями. Например, функция Дракина и Вуевского (1940 г.) содержит три параметра (A, x, m) [5] и представлена как.

.

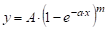
В таком виде эту функцию можно считать функцией «Митчерлиха». За последние 80 лет она получила положительную оценку и используется для моделирования таксационных показателей.

Дифференциальные уравнения для моделирования закономерностей в различных областях науки и сегодня привлекают ученых для создания и доказательства «Общих моделей роста».

Так функция Верхалста — Перла [6] имеет вид:

.

которое используется для описания плотности популяции, это уравнение было получено при решении дифференциального уравнения:

.

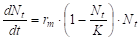
где Nt — численность популяции в момент времени t;

K — максимальная численность популяции;

N0 — плотность популяции при t=0;

rm — мера внутренней способности популяции к численному росту.

Уравнение Гомпертца представлено как.

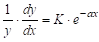
и используется для описания роста животных.

В 1920 г. Пюттер А. предположил, что увеличение веса животных определяется двумя противоположными процессами (синтезом и распадом). К таким же выводам (скорость роста животных пропорциональна разности между поверхностью и объёмом тела) пришли Винберг Г. Г. (1966), Зотин А. И. (1974), который вывел уравнение роста животных [4].

Шолохов А.Г. (2000) предложил уравнение для описания всех таксационных показателей (кроме густоты) [11]. Он предполагал, что силы роста линейные, а силы противодействия росту — нелинейные.

Логическое рассмотрение процесса, явления в экосистеме позволяет построить общие дифференциальные модели роста, а их решение, представленное в алгебраическом виде дает модель для исследования конкретных локальных задач.

Знания о закономерностях изменения таксационных показателей отдельного дерева во времени дают основания для характеристики динамики роста и развития древостоев. Для решения этой задачи использовали методику полного анализа хода роста древесного ствола, которая подробно приведена в книге «Таксация леса» [12].

Для полного анализа хода роста древесного ствола были проведены полевые измерения 21 модельного дерева. Камеральная обработка экспериментальных данных проведена по программе «Xod» [1, 13].

Программа «Xod» является инструментом исследователя для ввода, обработки и хранения исходной и расчетной информации при проведении полного анализа хода роста древесного ствола (ПАХРДС). Интерфейс программы и пример по модельному дереву приведены на рисунке 1.

Результаты обработки экспериментальных данных по модельному дереву записываются в базу данных и служат для дальнейших статистических расчетов.

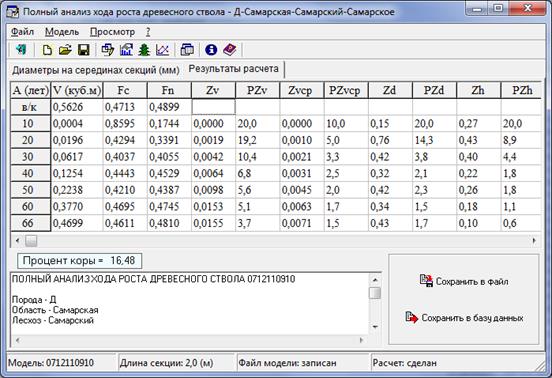
Рисунок 1. Результаты расчета динамики таксационных показателей по модельному дереву.

Отметим, что использование математической модели для восстановления хода роста древесного ствола в высоту дает высокую точность по сравнению с линейной интерполяцией, но при этом требуются дополнительные затраты времени от исследователя на поиск и анализ моделей.

Анализ известных функций роста показывает, что ход роста живых организмов можно описать множеством функций роста с различной точностью. Наши расчеты доказывают, что для моделирования динамики таксационных показателей древостоев хорошие результаты дает функция Э. А. Митчерлиха [2, 8, 9, 13]. Эта функция удовлетворяет всем необходимым требованиям.

Функция имеет вид:

.

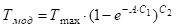
где Тмод — моделируемый таксационный показатель, например, высота, м;

Тmax — асимптотическое значение таксационного показателя для данного естественного ряда развития древостоя;

A — возраст, лет;

e — основание натурального логарифма;

С1 — параметр роста;

С2 — параметр формы кривой.

Кривая роста имеет S-образный вид при С2 > 1 и хорошо описывает значение высот.

Для выявления временного ряда хода роста диаметров и высот отдельных деревьев дубрав искусственного происхождения рассчитаем параметры функцией роста Митчерлиха.

При расчете параметров функции Митчерлиха нами приняты в качестве аргументов возраст и диаметр на высоте 1,3 м.

Рисунок 2. Радиальный срез для исследования хода роста по радиусу отдельного ствола лесных культур дуба, пробная площадь № 2, модельное дерево № 1.

На рисунке 2 приведен пример измерения величины годичного прироста по радиусу древесного ствола дуба в камеральных условиях, используя масштабируемое изображение.

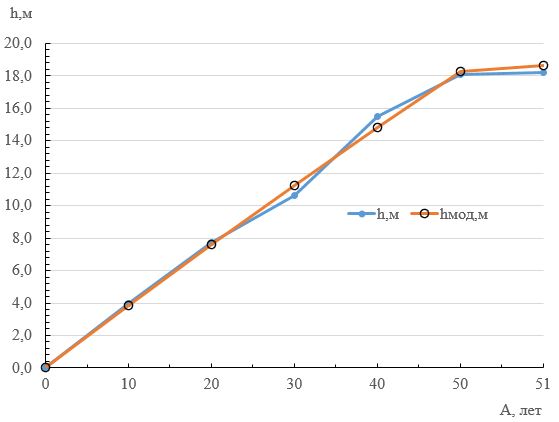
Рисунок 3. Экспериментальные и модельные значения хода роста по высоте отдельного ствола лесных культур дуба, пробная площадь № 9, модельное дерево № 1.

Как показывает график (рис. 3), выровненная кривая хода роста по высоте (hмод) с использованием функции Митчерлиха с высокой точностью совпадает с экспериментальными значениями (h). Полученные модели (таблица 1) по материалам измерений модельных деревьев дуба, характеризующие значения высот в зависимости от возраста и диаметра, а также взаимосвязь диаметров деревьев и их возраста имеет высокую адекватность (множественный коэффициент детерминации находятся в пределах от 0,967 до 0,999).

Моделирование таксационных показателей по результатам измерений по методике полного анализа хода роста отдельного дерева подтверждает правильность выбора функции Митчерлиха для предсказания соотношений высот и диаметров в зависимости от возраста, а также высот от диаметров.

Таблица 2. Математические модели соотношений высот и диаметров стволов дуба по материалам полного анализа хода роста древесного ствола.

№ п/п.	№ модели.	Независимые факторы.	Параметры моделей.	Коэффициент детерминации, R2.
			d max.	C1.	C2.
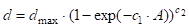		А.	38,11.	— 0,0239.	1,6380.	0,988.
		А.	22,44.	— 0,0686.	3,0869.	0,999.
		А.	452,66.	— 0,0030.	1,5635.	0,995.
		А.	328,24.	— 0,0057.	2,1764.	0,998.
		А.	33,88.	— 0,0293.	1,7584.	0,989.
		А.	22,44.	— 0,0680.	3,0869.	0,999.
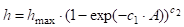№ п/п.	№ модели.	Независимые факторы.	Параметры моделей.	Коэффициент детерминации, R2.
			h max.	C1.	C2.
		А.	21.47.	— 0,0360.	1,6090.	0,999.
		А.	13,5824.	— 0,0629.	1,9902.	0,999.
		А.	21,351.	— 0,0377.	1,3590.	0,998.
		А.	18,01.	— 0,0506.	3,1068.	0,967.
		А.	22,11.	— 0,0435.	1,9042.	0,978.
		А.	15,02.	— 0,0467.	1,5764.	0,993.
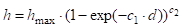№ п/п.	№ модели.	Независимые факторы.	Параметры моделей.	Коэффициент детерминации, R2.
			h max.	C1.	C2.
		d.	107,432.	— 0,0046.	0,8110.	0,987.
		d.	76,0091.	— 0,0039.	0,7125.	0,996.
		d.	23,6239.	— 0,0409.	0,5960.	0.992.
		d.	58,8739.	— 0,0064.	0,6198.	0.990.
		d.	169,512.	— 0,0040.	0,9021.	0.989.
		d.	76,0091.	— 0,0039.	0,7125.	0.996.

При моделировании лесотаксационных закономерностей древостоя элемента леса обоснованно используются функции роста: степенная, экспоненциальная, модифицированная экспоненциальная, логистическая, функция Гомпертца, гиперболическая экологическая, Митчерлиха, запаздывающая квазилогистическая и др.

Для разработки таблиц хода роста мы приняли методику, предложенную Черных В. Л. [12], которая базируется на основе функции роста Митчерлиха с изменяющимися параметрами в динамике.

Опираясь на анализ функций роста и существующий опыт многих исследователей для составления моделей и таблиц хода роста древостоев различной густоты мы разработали следующий алгоритм.

• 1. Формируется база данных по лесорастительному району по материалам пробных площадей и массовой таксации выделов и древесной породе. Основные показатели: тип леса, тип лесорастительных условий, возраст (лет), высота (м), диаметр (см), запас (м3), сумма площадей сечений (м2).
• 2. Рассчитываются статистические показатели: дисперсия и коэффициент изменчивости возраста, высоты, диаметра, запаса, суммы площадей сечений.
• 3. Выявляется взаимосвязь изменчивости суммы площадей сечений с возрастом и высотой элемента леса.
• 4. Выявляется влияние густоты на рост по высоте и диаметру элемента леса.
• 5. Рассчитывается интервальная оценка показателя суммы площадей сечений древостоя с вероятностью 0,68 (t = 1,0 — критерий Стьюдента) по каждой средней высоте, группе густоты и в исследуемом возрасте: для густых уравнение имеем вид:

.

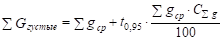
для редких.

.

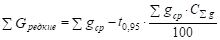
где, УGзначение суммы площадей сечений древостоя в исследуемом возрасте с вероятностью 0,68, м2;

Уgср — экспериментальное значение суммы площадей сечений древостоя в исследуемом возрасте, м2;

СУg — расчетное среднее значение изменчивости суммы площадей сечений древостоя в исследуемом возрасте, %.

• 6. Для каждой группы густоты формируется база исходных и расчетных показателей: возраст (лет), высота (м), диаметр (см), запас (м3), сумма площадей сечений (м2).
• 7. Проводится автоматизированное построение модели хода роста древостоя по программе «MICHXOD» [13]
• 8. Выполняется анализ и оценка результатов моделирования хода роста древостоя элемента леса (точность, корректность, адекватность).
• 9. Представление модели хода роста в табулированном виде с заданным шагом (1, 5 или 10 лет).

Практическая реализация этого алгоритма нами выполнена на материалах пробных площадей (таблица 1) и массовой таксации выделов (331 шт.).

По экспериментальным материалам получены следующие уравнения связи, отражающие влияние густоты древостоя элемента леса на таксационные показатели лесных культур дубняков Нижнего Поволжья.

Изменчивость суммы площадей сечений древостоя на 1га.

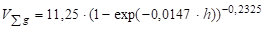
r=0.72;

Влияние густоты (n) возраста (a) и абсолютной полноты (g) на значения средних высот (h) и средних диаметров (d) древостоя элемента леса имет вид:

r=0,94;

r=0,97.

Показатели суммы площадей сечений древостоя с вероятностью 0,68 (t = 1,0 — критерий Стьюдента) по каждой группе густоты.

.

.

.

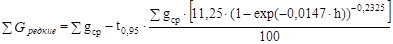
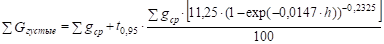
Система уравнений таблиц хода роста по группам густоты приведена в таблице 3.

Таблица 3. Математические модели хода роста дубняков искусственного происхождения Нижнего Поволжья.

Уравнение по группам густоты.
группа густотыредкие.
	0,02.
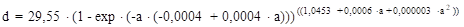	0,03.
	0,18.
	0,19.
группа густоты — средние.
	0,02.
	0,02.
	0,22.
	0,15.
группа густоты — густые.
	0,04.
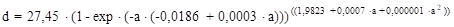	0,07.
	0,48.
	0,79.

Таблица 4. Хода роста модальных дубняков искусственного происхождения Нижнего Поволжья, лесорастительная зона — Район степей европейской части Российской Федерации, группа густоты — редкие.

Хода роста модальных дубняков искусственного происхождения Нижнего Поволжья, Лесорастительная зона — Район степей европейской части Российской Федерации, группа густоты — средняя.

Хода роста модальных дубняков искусственного происхождения Нижнего Поволжья Лесорастительная зона — Район степей европейской части Российской Федерации, группа густоты — густые.

Полученная система уравнений в целом характеризует ход роста в динамике по группам густоты. Как видно из таблицы 4 остаточная дисперсия по моделируемым таксационным показателям оказалась минимальной, а множественный коэффициент детерминации находится в пределах от 0,94 до 0,99.

Таблица 5. Оценка новых таблиц хода роста дубняков искусственного происхождения Нижнего Поволжья средней густоты по стандартным таблицам В/О Леспроект и по А. Д. Дудареву [9].

Как показали исследования, по существующим нормативам «В/О Леспроект» [9] обеспечивается определение относительной полноты, а следовательно и запаса с систематической ошибкой в -8,4 .+9,0%, а по таблицам А. Д. Дудареву -33,5.+7,2.

Таким образом, новые таблица хода роста повышают точность оценки запаса и полноты. Новые нормативы рекомендуются для оценки производительности дубовых насаждений искусственного происхождения Нижнего Поволжья.

Выводы Анализ функции роста применяемых для исследования живых организмов позволил для описания лесотаксационных закономерностей отдельного дерева и древостоя элемента леса рекомендовать функцию Митчерлиха.

Предложен алгоритм для составления моделей и таблиц хода роста древостоев различной густоты.

На основе экспериментальных данных выявлено закономерное влияние природных факторов на производительность насаждений при различной густоте, разработаны математические модели и таблицы хода роста.

Максимальная продуктивность в редких дубняках наступает в 43 года, а в густых в 46 лет.

Выявлено, что снижение продуктивности в редких дубняках наступает в 65 лет, а в густых в 67 лет.

Общая производительность дубняков Нижнего Поволжья искусственного происхождения начинается снижаться в 35−40 лет.

Проведенные исследования показали, что дубняки искусственного происхождения Нижнего Поволжья в зоне степей европейской части Российской Федерации характеризуются специфическими закономерностями по производительности древостоев и динамике таксационных показателей по сравнению с лесостепной зоной. Поэтому необходимо рекомендовать производству для оценки лесных ресурсов использовать региональные лесотаксационные нормативы.

Предлагаемые к внедрению в производство таблицы хода роста позволяют повысить точность лесоучетных работ на 8−12%.

дерево лес рубка насаждение.

• 1. А.с. 2 000 610 864 РФ. Полный анализ хода роста древесного ствола / С. В. Баранов, В. Л. Черных (РФ); № 2 000 610 740 / Заявл. 11.07.2000; зарегистр. 08.09.2000.
• 2. Моделирование динамики древостоев на фазе разрушения / С. В. Веневский, А. З. Швиденко // Устойчивое развитие бореальных лесов: тр. VII ежегод. конф. МАИБЛ. — М.: Рослесхоз, 1997. — С. 30−33.
• 3. Загреев В. В. Географические закономерности роста и продуктивности древостоев / В. В. Загреев. — М.: Лесн. пром-сть, 1978. — 240 с.
• 4. Зотин А. И. Термодинамический подход к проблемам развития, роста и старения / А. И. Зотин. — М.: Наука, 1974.-184 с.
• 5. Кузьмичев В. В. Закономерности роста древостоев / В. В. Кузьмичев. Ин-т леса и древесины СО АН СССР. — Новосибирск: Наука, 1977. — 160 с.
• 6. Математическое моделирование: [пер. с англ.] / под ред. Ю. П. Гупало. — М.: «МИР», 1979. — 277 с.
• 7. Майоров С. Л. Влияние густоты посадки культур на формирование густоты насаждений, их рост и продуктивность: сб. работ / С. Л. Майоров // Исследования по лесной таксации и лесоустройство леса. — М.: — Лесн. пром-сть, 1968. — С. 81−89.
• 8. Митчерлих Э. А. Почвоведение: [пер. с нем.] / Э. А. Митчерлих — под ред. Э. И. Шконде. — М., 1957. — 416 с.
• 9. Нормативы для таксации лесов центрального и южного районов европейской части Российской Федерации: (Справочник) / Рослесхоз. — М.: Центрлеспроект, 1993. 418 с.
• 10. Швиденко А. З. Таблицы и модели хода роста и продуктивности насаждений основных лесообразующих пород Северной Евразии: нормативно-справочные материалы / А. З. Швиденко, Д. Г. Щипащенко, С. Нильссон, Ю. И. Булуй. — 2-е изд., доп. — М.: Рослесхоз, Международный институт прикладного системного анализа, -2008. — 886 с.
• 11. Шолохов А. Г. От закономерностей к закону роста леса / А. Г. Шолохов — Пушкино: ВНИИЛМ, 2000. -183 с.
• 12. Черных В. Л. Информационные технологии в лесном хозяйстве: учеб. Пособие / В. Л. Черных, В. В. Сысуев. — Йошкар-Ола: МарГТУ, 2000. — 378 с.
• 13. Черных В. Л. Информационные технологии в лесном хозяйстве: учеб. пособие / В. Л. Черных, [и др.] - Йошкар-Ола: МарГТУ, 2009. — 144 с.
• 14. Assmann E. and Franz F. Vorlдufige Fichten-Ertragstafel fьr Bayern. Institut fьr Ertragskunde forstliche Forschungsanstalt Mьnchen, Mьnchen, 1963. 112 p.