Модель урожайности сельскохозяйственных культур в технологии точного земледелия

Модель урожайности сельскохозяйственных культур в технологии точного земледелия

Программные пакеты географических информационных систем (ГИС) играют решающую роль при построении и анализе карт в точном земледелии. В первую очередь ГИС предназначены для хранения и обработки данных и представлены дифференциальной глобальной системой позиционирования (данные об урожайности, точках взятия проб, границ полей и др.), обеспечивающей составление тематических карт разного назначения (обработка почвы, посев, удобрение, борьба с вредными организмами и др.). Современные ГИС интегрируют информацию трех уровней: карты, модели и базы данных, — содержащую подробные сведения о конкретных точках в пространстве [9, с. 55].

Крупномасштабные цифровые данные о рельефе сельскохозяйственных земель сегодня есть на ограниченную территорию. Переход на цифровую основу упростит формирование картограмм свойств почв непосредственно по результатам полевого обследования [1, с. 13].

Основой построения современных информационных систем сельскохозяйственного производства также являются навигационные системы, в первую очередь за счет необходимости использовать земельно-информационные системы, обеспечения сантиметровой точности и представления информации для работы исполнительными механизмами [2, с. 17].

Анализ источников. Технология точного земледелия осуществляется оборудованием машинно-тракторных агрегатов с автопилотами и системами параллельного вождения, которые позволяют свести к минимуму влияние человеческого фактора при выполнении агротехнологических операций, а также значительно увеличить производительность техники [4, с. 36].

На основе полученных данных составляется электронная карта, с помощью которой уточняются границы территории хозяйства, а также реальная площадь. Электронная карта позволяет контролировать все сельскохозяйственные операции, поскольку опирается на точные знания площадей полей, протяженности дорог и расположения объектов [3, с. 12].

Электронная карта позволяет дойти до каждого земельного участка, который используется в хозяйстве, вне зависимости от его размера [7, с. 48].

Кроме того, она помогает провести более полный анализ условий, влияющих на рост растений на конкретном поле или даже на его участках размером 10Ч10 м. Такую карту можно использовать для учета севооборота, т. е. внутрихозяйственного землеустройства, мониторинга подвижных объектов, организации перевозок, картирования урожайности, исследования почв, статистического и тематического анализа данных, а также планирования производственного процесса.

Благодаря подробному почвенному обследованию с GPS-привязкой можно определить потребность в питательных элементах, а также другие агрохимические показатели с точностью до 1 м и впоследствии составить технологическую карту для дифференцированного внесения удобрений. Для этих целей можно использовать программное обеспечение MapInfo, SSToolBox, ArcGIS и др., которое позволяет создать карту распределения основных питательных элементов в почве. Впоследствии она используется при составлении технологической карты для дифференцированного внесения удобрений [3, с. 12].

Составление такой карты возможно на основе модели урожайности зерновых, устанавливающей зависимость их урожайности от соответствующих факторов. Такую модель можно построить методом линейного регрессионного анализа с использованием центрирования данных [8, с. 322]. В других источниках он рассматривается как метод коллокации [6, с. 63].

Методы исследования. Задачу сформулируем следующим образом.

Будем считать, что урожайность зерновых — сигнал, который зависит от следующих факторов — исходных данных (импульсов): нормы внесения калия, фосфора, кислотности почв.

Необходимо установить зависимость сигналов от импульсов и по необходимому значению сигнала вычислить значения импульсов, т. е. по требуемому значению урожайности в данной точке рассчитать значения факторов.

Примем следующие обозначения: S — урожайность, l₁ — кислотность почвы (РН), l₂ — норма внесения фосфора, l₃ — норма внесения калия. Три последние величины — факторы, определяющие урожайность.

Построение модели урожайности будем иллюстрировать на конкретном примере. Так, в таблице в столбцах РН, фосфор, калий, урожайность приведены значения влияющих факторов и урожайности для десяти контрольных участков, расположенных равномерно по всему полю. По этим данным необходимо построить модель урожайности.

Таблица. Исходные данные.

В данной задаче n значениям факторов тоже соответствует n значений урожайности, как следует из блочного выражения (1):

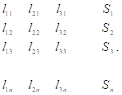
(1).

В (1) все величины центрированы и представлены в виде соответствующих разностей в таблице. Для удобства дальнейшего изложения введем обозначения:

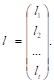
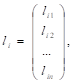
(2).

В (1) и (2) l_ik, S_k ? экспериментальные значения величин l_i и S при измерении k от 1 до n.

Для решения задачи необходимо иметь как корреляционную матрицу вектора факторов l, так и совместную корреляционную матрицу этого вектора и урожайности S. Эти матрицы можно получить статистически на основе данных из таблицы 1. В общем виде корреляционная матрица факторов может быть записана так:

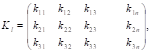
(3).

где t _ число факторов, k_ij _ корреляционный момент между факторами i и j, вычисляемый по формуле:

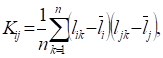
(4).

где.

(5).

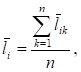
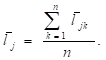
(6).

Выражениям (5) и (6) соответствуют средние значения в таблице, а разности выражения — (4) столбцам «Разности» в таблице 1.

Полная корреляционная матрица вектора факторов l и сигнала S записывается так:

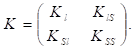
(7).

В матрице (7).

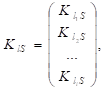
(8).

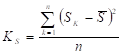
(9).

а.

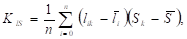
(10).

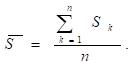
(11).

В общем случае линейную модель урожайности можно записать так:

(12).

где.

(13).

H? вектор неизвестных параметров, подлежащих оцениванию, а вектор l в линейном регрессионном анализе называется регрессором или предиктором [8, с. 49]. Там же S называется откликом.

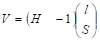
(14).

Для определения вектора H запишем следующую разность:

(15).

Корреляционная матрица или дисперсия скалярной величины V будет следующая:

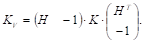
(16).

После подстановки матрицы (7) в (16) получим:

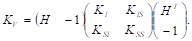
(17).

А после перемножения матриц получим выражение дисперсии величины V:

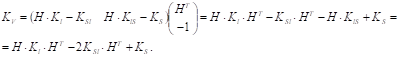
(18).

Для достижения минимума дисперсии выражение продифференцируем по H^T и приравняем полученную производную нулю:

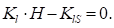
(19).

Тогда из (19) непосредственно находим:

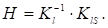
(20).

После подстановки (20) в (12) получаем аналитическое выражение модели урожайности:

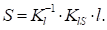
(21).

Расчет дифференциального внесения удобрений. В соответствующей точке поля, в которой известны значения L? наблюдаемые (натуральные) значения регрессоров, расчеты выполним в следующем порядке:

• — задаваясь требуемым значением S, определяем вектор, обозначаем его через L_T;
• — вычисляем разность L_T _ L, которая и определяет величину дифференциального внесения удобрений в данной точке поля:

(22).

Пример расчета модели урожайности и дифференциального внесения удобрений:

В соответствии с (3) и (7) матрица К будет:

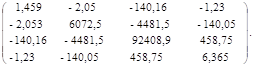
(23).

В матрице (23) верхний блок размером 3*3 соответствует матрице K_l:

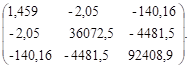
(24).

Тогда матрица K_l^-1 будет:

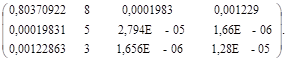
(25).

Вектор K_Sl в данном случае имеет вид:

(26).

Тогда в соответствии с (21) найдем:

(27).

Поскольку в данной работе осуществляется центрирование данных, то полная модель урожайности будет:

(28).

Средняя квадратическая ошибка модели составляет 0,7 единиц урожайности. урожайность сельскохозяйственный культура удобрение.

Расчет дифференциального внесения удобрений. Выполним теперь расчет дифференциального внесения удобрений для первой точки поля (таблица). Для этого вначале вычислим модельную урожайность в этой точке.

Для нее.

(29).

S? это среднее значение урожайности в табл. 1.

Тогда на основе (28) найдем:

S=44.5+0,39=44,89. (30).

Это модельная урожайность в данной точке.

Рассмотрим возможность повышения урожайности за счет изменения значений факторов. Определим дифференциальные значения внесения удобрений для достижения максимально возможной урожайности в данной точке.

Для продолжения решения запишем аппроксимирующую модель [8, с. 323]:

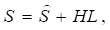
(31).

где.

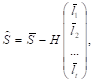
(32).

а? не центрированные, а средние наблюдаемые значения регрессоров, а L — тоже вектор не центрированных, а наблюдаемых значений факторов.

В нашем случае имеем:

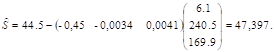
(33).

Тогда в соответствии с (31) и (33) запишем:

(34).

Подставляя значения Н из (29) и L для первой точки, равное:

(35).

найдем:

что полностью согласуется с (30).

Теперь рассчитаем дифференциальное значение внесения удобрений с целью максимально возможного подъема урожайности.

Для этого уравнение регрессии (34) запишем в развернутом виде:

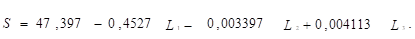
(36).

Из него следует, что урожайность можно поднять за счет снижения кислотности (L₁), снижения фосфора (L₂) и повышения количества калия (L₃). Понизим кислотность на 2 единицы, содержание фосфора нельзя понизить, но содержание калия повысим на 200 единиц. Тогда вектор дифференциального регулирования факторов составит.

(-2,0 0 +200).

Изменение факторов должно находиться в оптимальных пределах, рекомендованных соответствующими методическими указаниями [5, с. 9]. Наши значения соответствуют указанным пределам. При данном дифференциальном регулировании значения L₁, L₂, L₃ будут соответственно равны: 3,5; 217; 376.

Тогда в соответствии с моделью (36) найдем максимально возможную урожайность: 46,62. Это на 2,12 больше фактической урожайности. Как видим, урожайность можно увеличить в научно обоснованных пределах.

Отметим, что модель (34), (36) может быть получена в среде Excel по команде:

Формулы > Другие функции > Статистические > Линейная.

Но полученные данные дают лишь полученные данные линейной регрессии без установления корреляционных зависимостей между факторами. Отметим также, что применение пакета Excel без постоянной константы приводит вообще к неверным результатам. Так, при обоснованной точности модели в 0,7 единицы урожайности результаты в среде Excel давали результаты в 4 единицы урожайности, что недопустимо.

Заключение

• 1. Новизной работы является то, что модель урожайности предлагается получать по корреляционным зависимостям между урожайностью и факторами.
• 2. На основе центрирования данных можно построить модель урожайности как основы дифференциального внесения удобрений при точном земледелии. Преимущество такого подхода заключается в использовании корреляционных зависимостей для определения неизвестных параметров линейной регрессии.
• 3. Для вычисления дифференциальных показателей внесения удобрений в данном алгоритме осуществляется переход к аппроксимирующей модели. При этом построены две такие модели (28) и (34), (36). Они приводят к одним и тем же результатам, но значительно расширяют теоретическую базу статистического анализа для дифференциального решения задач в точном земледелии по сравнению с программным пакетом, содержащимся в среде Excel.

• 1. Бобер, Н. П. Использование земельно-информационной системы при подготовке плановой основы для целей точного земледелия / Н. П. Бобер, М. П. Богданович // Внедрение информационных систем, использующих спутниковую навигацию, в технологиях аграрного комплекса. Опыт и перспективы: материалы Междунар. науч.-технич. конф. — Гомель: ГКНТ, 2010. — С. 13−16.
• 2. Демьяненко, А. В. Проблемы внедрения навигационно-информационных технологий в сельскохозяйственном производстве / А. В. Демьяненко, В. М. Кирсанов // Внедрение информационных систем, использующих спутниковую навигацию, в технологиях аграрного комплекса. Опыт и перспективы: материалы Междунар. науч.-технич. конф. — Гомель: ГКНТ, 2010. — С. 17−20.
• 3. Жукова, О. А. Точность на полях / О. А. Жукова // Агропрофи. — 2008. — № 3 — С. 12−34.
• 4. Клочков, А. В. Возможности применения курсоуказателей с системой GPS / А. В. Клочков, А. Е. Маркевич // Белорусское сельское хозяйство. -2009. — № 11. — С. 36−43.
• 5. Кузнецов, Г. И. Кадастровая оценка земель сельскохозяйственных предприятий: методические указания / Г. И. Кузнецов, Г. М. Мороз // Государственный комитет по земельным ресурсам, геодезии и картографии Республики Беларусь. — Минск, 2001. — 116 с.
• 6. Мориц, Г. Современная физическая геодезия / Г. Мориц. — М.: Недра, 1988 — 392 с.
• 7. Нестеровский, Е. А. Использование электронных карт для целей точного земледелия на основе земельно-информационной системы (ЗИС) локального уровня / Е. А. Нестеровский, Д. А. Чиж, С. П. Бунько // Внедрение информационных систем, использующих спутниковую навигацию, в технологиях аграрного комплекса. Опыт и перспективы: материалы Междунар. науч.-технич. конф. — Гомель: ГКНТ, 2010. — С. 48−53.
• 8. Себер, Дж. Линейный регрессионный анализ / Дж. Себер. — М.: Мир, 1980 — 452 с.
• 9. Шпаар, Д. Точное сельское хозяйство (Precision agriculture): учеб.-практ. пособие / Д. Шпаар, Д. Захаренко, В. Якушев. — СПб.-Пушкин, 2009. — С. 397.