Теоретические основы исследования рабочих органов на основе моделирования процесса вторичной сепарации в картофелеуборочных машинах

Аннотации

В статье рассмотрены теоретические основы исследования рабочих органов на основе моделирования процесса вторичной сепарации в картофелеуборочных машинах.

The article deals with the theoretical base of the research work on the basis of modeling of secondary separation in a potato harvester.

Ключевые слова: картофель, клубень, картофелеуборочный комбайн.

Keywords: pоtatо, tuber, potato harvester.

По данным многочисленных исследований [1, 2, 3, 4], на современном этапе развития техники для уборки картофеля одной из актуальных научно-технических задач является совершенствование процесса и средств вторичной сепарации картофелеуборочных машин. Известно достаточно большое количество схемно-конструктивных решений органов выносной сепарации, в том числе разработанных с участием авторов данной статьи. Данные решения позволяют снизить повреждения и потери клубней в уборочной машине, а также повысит эффективность разделения примесей в первую очередь за счет использования клубнеотражателей с эластичными рабочими элементами, контактирующими с клубнями, а также за счет изменения углов их взаимного действия [5, 6, 7, 8]. Для рационализации выбора параметров и регулировок рабочих элементов современных сепарирующих органов нами предлагается описанная ниже методика, основанная на моделировании процесса вторичной сепарации, позволяющая связать воедино основные конструктивные и кинематические параметры данных устройств.

Основным критическим фактором примем максимально допустимое значение напряжения, возникающее при взаимодействии клубня с боковой поверхностью эластичного рабочего элемента. Будем считать, что пока это значение не превышено, повреждения клубней не поднимутся выше уровня, установленного агротехническими требованиями.

При расчете примем следующие допущения. Будем считать: клубни движутся сплошным равномерно распределенным по ширине полотна горки потоком; масса клубней, приходящихся на одну лопасть клубнеотражателя, соизмерима с массой лопасти. Поэтому при их взаимодействии будем учитывать массу клубней и массу лопасти.

Рассмотрим наиболее неблагоприятный случай взаимодействия. Наибольшая ударная нагрузка между клубнями и лопастью будет в положении, когда лопасть перпендикулярна плоскости полотна горки, т.к. в этом положении скорость клубня по отношению к лопасти достигает максимального значения.

Рассмотрим кинематику движения клубня и лопасти до удара лопасти о клубень (рисунок 1).

Рассмотрим наиболее неблагоприятный случай, при котором клубень с прикрепленным к ней столоном и неоторванной ботвой движется поступательно со скоростью вместе с полотном горки. Будем считать, что ботва жестко связана с полотном горки и беспрепятственно проходит под лопастью отбойного валика.

Пластина, жестко закрепленная на валу, отстоит от оси вращения вала на расстоянии R и составляет с ней угол в. Отбойный валик расположен горизонтально и его ось параллельна полотну горки. Следовательно, нижняя кромка лопасти будет параллельна плоскости полотна горки в положении, когда лопасть перпендикулярна полотну горки. Таким образом, зазор b между полотном горки и лопастью одинаков по всей ширине лопасти.

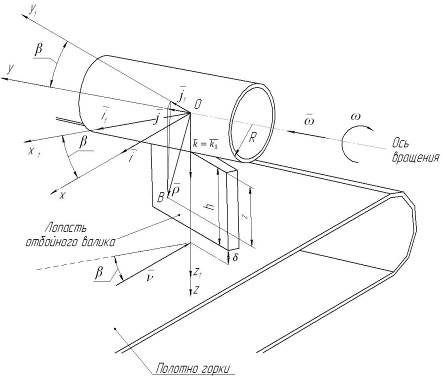
в — угол между лопастью и осью отбойного валика, рад; ох 1у 1z1 — система координат, связанная с лопастью; ось ох перпендикулярна оси вала, ось ох 1 перпендикулярна плоскости лопасти отбойного валика; R — расстояние от оси отбойного валика до верхнего края лопасти, м; z — расстояние от верхнего края лопасти до произвольной точки В лежащей в её плоскости, м; д — рабочий зазор, м.

Рисунок 1. Схема взаимодействия лопасти и клубня.

Найдем скорость произвольной точки B лопасти при вращении лопасти с угловой скоростью щ вокруг оси отбойного валика.

Радиус-вектор точки B: картофелеуборочный лопасть клубень.

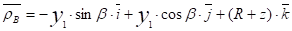
(1).

Вектор угловой скорости лопасти:

(2).

где: — единичные орты осей ох, оу, оz соответственно.

Тогда вектор скорости точки B равен:

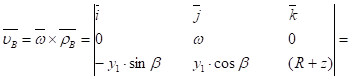
(3).

Проекции вектора скорости на оси ох 1, оу 1, оz1 равна скалярному произведению на единичные орты этих скоростей:

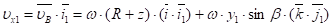
Из рисунка 2 следует, что,. Окончательно имеем:

(4).

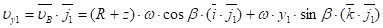
Из рисунка 1 следует, что;. В результате имеем:

(5).

Так как, , то будем считать, что перемещение при изгибе пластины малы по сравнению с высотой лопасти h.

(6).

Так как лопасть испытывает косой удар по нижней кромке, то изгиб можно представить происходящим в двух плоскостях ох 1z и оу 1z (рисунок 2).

Уравнение изогнутой оси лопасти в плоскости ох 1z можно получить, используя уравнение начальных параметров:

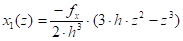
(7).

где: fx — максимальный прогиб в направлении оси ох 1, м Уравнение изогнутой оси лопасти в направлении оси оу 1 имеет аналогичный вид:

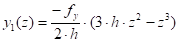
(8).

где: fy — максимальный прогиб в направлении оси оу 1, м Здесь принято, что лопасть жестко прикреплена к валу отбойного валика.

Является общепринятым допущение о пропорциональности скоростей точек оси прогибов:

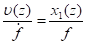
Отсюда можно выразить скорость произвольного сечения лопасти при изгибе по направлению оси ох 1:

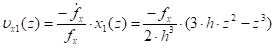
(9).

Аналогично имеем скорость произвольного сечения лопасти при изгибе по направлению оси оу 1:

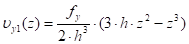
(10).

Знак «-» в (9) означает, что скорости точек лопасти при её изгибе направлены в отрицательную сторону оси x1.

Ударное взаимодействие клубня с лопастью в 1-ой фазе удара будем считать абсолютно неупругим, т. е. после первой фазы удара, когда клубень получает часть энергии лопасти, он не отскакивает от лопасти, а вместе с ней продолжает движение.

Согласно равенствам (5 — 10) скорость произвольной точки B лопасти в начале второй фазы удара будет равна:

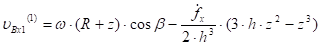
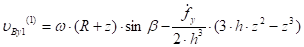
(11).

В равенстве неизвестными являются скорости точки в месте удара при изгибе лопасти и .

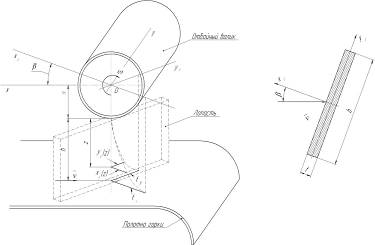
z — текущая координата поперечного сечения лопасти; h — высота лопасти, м; x1(z) — перемещение точки оси лопасти с координатой z по направлению оси x1, м; у 1(z) перемещение точки оси лопасти с координатой z по направлению оси у 1, м; , — аналогичные перемещения в месте удара клубня о лопасть, м; оси ox1, oy1 — главные центральные оси инерции поперечного сечения; R — расстояние от оси вращения отбойного валика до лопасти; - вектор скорости клубня; b — ширина лопасти, м; t — толщина лопасти, м.

Рисунок 2. Схема деформирования лопасти при косом изгибе.

Так как клубни в начале второй фазы удара движутся вместе с точками нижней кромки лопасти, то проекции скорости клубней равны:

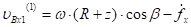
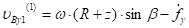
(12).

Скорости нижней точки оси лопасти и найдем, используя теорему Карно, согласно которой, потерянная кинетическая энергия системы клубень — лопасть за время первой фазы удара равна кинетической энергии потерянных скоростей клубня и лопасти.

Кинетическая энергия пластины до удара:

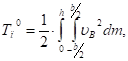
(13).

где: — масса элементарного объема лопасти толщиной t в точке B, кг;

г — объемный вес материала лопасти, Н/м 3.

Квадрат скорости точки B лопасти равен:

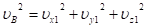
(14).

Подставляем (14) в (13) и используя выражения (4), (5), (6) получим:

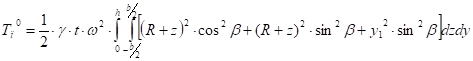
(15).

Вычисляя интегралы в (15) получим:

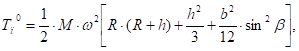
(16).

где: M — масса пластины, кг.

Кинетическая энергия клубней до удара:

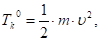
(17).

где: m — масса клубней по ширине лопасти, кг;

х — скорость клубней, движущихся вместе с лентой элеватора, м/с.

Кинетическая энергия лопасти в конце первой фазы удара равна:

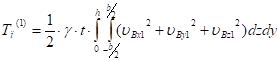
(18).

Подставим в (18) равенство (11):

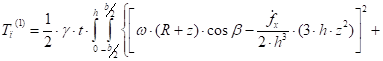
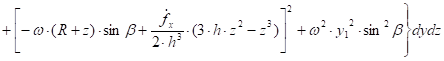
Выполняя интегрирование, получим:

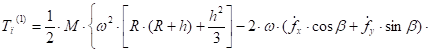
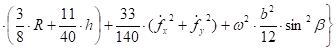
(19).

Кинетическая энергия клубней в конце первой фазы удара равна:

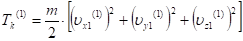
Подставим сюда равенство (12) и вычислим интеграл:

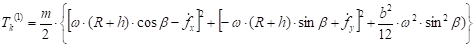
(20).

Потерянные скорости клубней и лопасти за время первой фазы удара — это разность между их скоростями до удара и их скоростями в конце первой фазы удара. Потерянные скорости клубней и лопасти найдем, используя равенства (5, 10, 11). Так, для лопасти имеем:

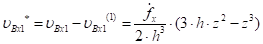
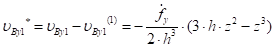
(21).

для клубня:

.

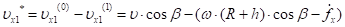
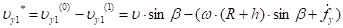
(22).

.

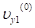
где:, , — проекции скорости клубней, движущихся вместе с полотном горки.

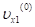
Кинетическая энергия потерянных скоростей лопасти равна:

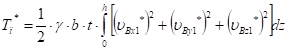
Подставим сюда равенства (21) и выполнив интегрирование, получим:

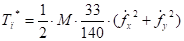
(23).

Кинетическая энергия потерянных скоростей клубня:

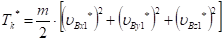
Подставим сюда равенство (22) и выполним интегрирование:

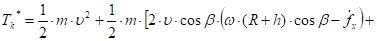
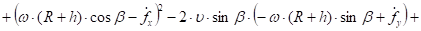
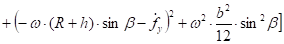
(24).

Согласно теореме Карно при неупругом ударе потерянная кинетическая энергия системы равна кинетической энергии потерянных скоростей:

(25).

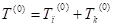
где: — кинетическая энергия системы до удара;

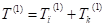
— кинетическая энергия системы в конце первой фазы удара;

— кинетическая энергия потерянных скоростей клубнями и лопастью.

С учетом этого уравнение (25) перепишем в виде:

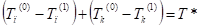
(26).

Вычислим разности в (26) и приведем их виду удобному для анализа полученного уравнения. Вычтем из равенства (16) равенство (19):

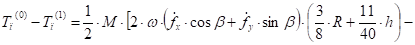
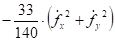
(27).

Вычтем из равенства (17) равенство (20):

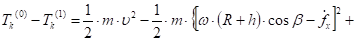
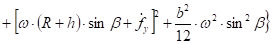
(28).

Подставим выражения (24), (27), (28) в равенство (26) и преобразуем полученное выражение к виду, удобному для анализа:

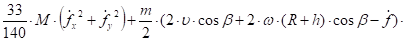
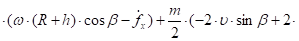
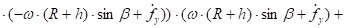
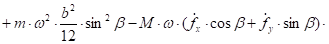
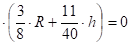
(29).

Сгруппируем величины, содержащие и по отдельности:

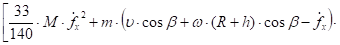
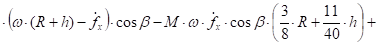
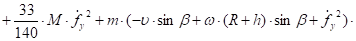
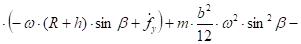
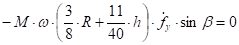
(30).

Выражения в квадратных скобках независимы друг от друга. Их сумма может равняться нулю, тогда и только тогда, когда каждые из этих выражений в квадратных скобках равны нулю. Таким образом, уравнение (29) равносильно двум уравнениям.

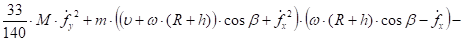
(31).

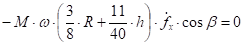
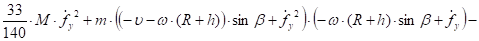
(32).

Раскроем скобки в (31) и (32) и сгруппируем подобные члены. В результате получим квадратные уравнения относительно и .

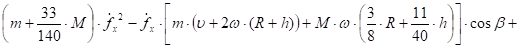
(33).

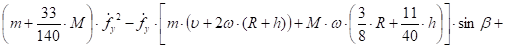
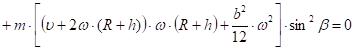
(34).

Решение уравнений (33) и (34) имеет вид:

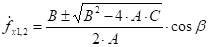
(35).

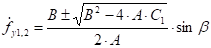
(36).

где: ;

;

;

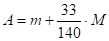
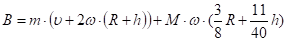
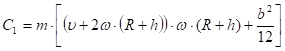
Чтобы определить знак перед корнем (35) и (36) рассмотрим случай, когда массой М лопасти можно пренебречь.

В этом случае:

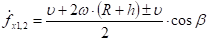
Если взять знак «+», то:

Если взять знак «-», то:

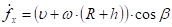
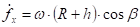
В безынерционной лопасти начальная скорость массы m равна относительной скорости массы m и точки удара массы о лопасть. Т. е.:

Следовательно, в решении (35) и (36) надо брать знак «+» .

Вычислив из (35) из (36) можно определить кинетическую энергию системы вначале второй фазы удара по равенствам (19) и (20).

Во второй фазе удара происходит деформация лопасти и натяжение столонов связывающих ботву с клубнями. Схематически деформированные состояния оси лопасти и растительных остатков изображены на рисунке 3.

Вторая фаза удара продолжается малый промежуток времени =(0,02−0,05) c, поэтому движение точки лопасти при ее повороте на угол ц=щ· ф можно считать происходящим по касательной к окружности с точностью до:

tan2ц? ц2.

Перемещение столона вместе с полотном горки (предполагается что ботва жестко связана с полотном горки):

(37).

Проекция полного прогиба на направление столона:

(38).

Перемещение точки В без учета деформации лопасти:

(39).

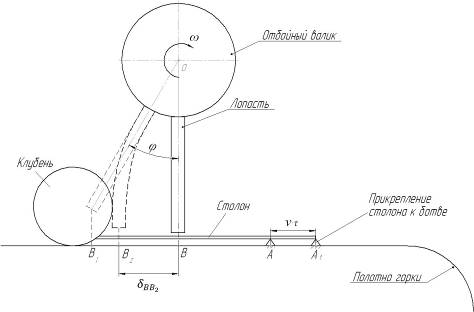
АВ — начальная длина столона; А 1 В 1 — длина столона в результате его деформации; В 1 В 2 — полный прогиб лопасти в месте соударения с клубнем; ох 1у 1 — главные центральные оси инерции поперечного сечения лопасти; АА 1 — перемещение столон вместе с полотном горки (предполагается что ботва жестко связана с полотном горки); BB1 — перемещение точки В без учета деформации лопасти.

Рисунок 3. Схема к определению удлинения корня клубня.

Поскольку жесткость лопасти в направлении оси х 1 существенно меньше жесткости в направлении оси у 1, то fx существенно больше fy и прогибы fx и fy малы по сравнению с длиной столона, то изменением направления столона за счет прогибов лопасти можно пренебречь. Тогда удлинение столона:

, (40)

где: (41).

Подставляя (37), (38),(39), (41) в (40), получим:

(42).

Уравнение (42) является уравнением совместимости деформаций лопасти и столона.

Удлинение столона можно выразить через продольную силу N в столоне соотношением:

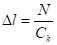
(43).

где: Ck — жесткость столона на растяжение, Н/м;

N — продольная сила в столоне, Н.

Прогибы лопасти можно выразить через усилия, с которыми клубни и столоны действуют на лопасть по известной из сопротивления материалов формуле для балки консоли.

Суммарные воздействия силы, с которой клубень действует на лопасть и усилие, действующее со стороны клубня N, равно силе Fп:

(44).

Проекции силы Fп на оси х 1, у 1 равны:

.

Прогибы в месте удара равны:

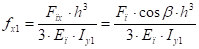
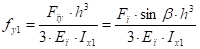
(45).

где: , — осевые моменты инерции поперечного сечения лопасти относительно осей х 1 и у 1 соответственно;

Еп — модуль упругости (модуль Юнга) материала лопасти.

Подставим (43) и (45) в уравнение совместности деформации (42):

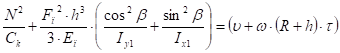
(46).

Второе уравнение для определения N и Fп получим используя теорему об изменении кинетической энергии в относительном движении во время второй фазы удара:

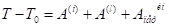
(47).

где: T, T0 — кинетические энергии относительного движения в конце и в начале второй фазы удара;

— работа внутренних сил;

— работа внешних сил;

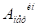
— работа сил инерции переносного движения.

В конце второй фазы удара прогиб достигает максимального значения, а скорость относительного движения равна нулю, следовательно:

T=0 (48).

В начале второй фазы удара прогиб достигает максимального значения, а скорости точек лопасти и клубней связанные со скоростями прогибов лопасти fx и fy определяются согласно равенствам (19) и (20):

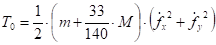
(49).

Работа внутренних сил:

(50).

где: U — потенциальная энергия деформации системы, т. е. лопасти и столонов.

Работа внешних сил А (l) (пренебрегая работой силы тяжести при ударе) равна нулю.

Работа сил инерции переносного движения Аперин при равномерном вращении плоскости также равна нулю, так как нормальная составляющая ускорения перпендикулярна перемещению точек лопасти и клубней.

В результате равенство (47) с учетом (48), (49), (50) принимает вид:

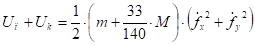
(51).

где: Uп, Uк — потенциальные энергии столонов и лопасти.

Потенциальная энергия деформации лопасти при косом изгибе равна:

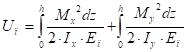
(52).

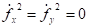
где: Мх, Му — изгибающие моменты в лопасти от силы Fп в момент когда скорость движения лопасти от изгиба равна нулю, т. е.. В этот момент на лопасть будет действовать максимальная сила давления Fп.

Изгибающие моменты равны:

, (53).

где: z — координата сечения, отсчитываемая от низа лопасти.

Подставляем (53) в (52) и интегрируя, получим:

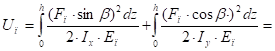
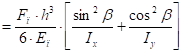
(54).

Столон, связывающий клубень с ботвой, работает на растяжение. Поэтому в пределах упругих деформаций:

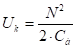
(55).

Подставим (54), (55) в выражение (47). В результате получим второе уравнение относительно Fп и N:

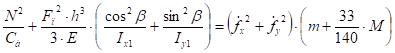
(56).

Систему уравнений (46), (56) запишем в виде:

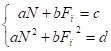
(57).

где:; ;

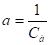
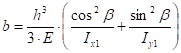
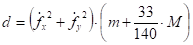
; (58).

Решение системы уравнений (57) может быть получено методом подстановки:

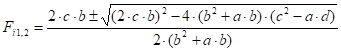
(59).

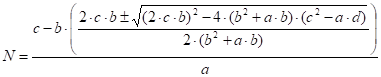
(60).

Сила взаимодействия клубней с лопастью:

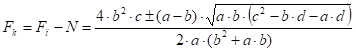
(62).

Сила действующая на один клубень:

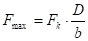
(63).

где: D — диаметр клубня, м.

Нормальные напряжения возникающие в клубне не должны превышать допускаемого напряжения [у].

Максимальные нормальные напряжения в клубне уmax можно определить, используя решение задачи Герца о давлении шара на плоскость. Это решение имеет вид:

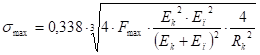
(64).

где: — сила нормального давления клубня на лопасть;

Rк — радиус клубня.

Условие прочности для клубня запишется в виде:

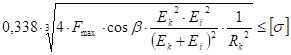
(65).

Из (65) находим допустимое значение силы [F]:

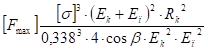
(66).

Сила взаимодействия клубня с лопастью в основном зависит от угловой скорости вращения отбойного валика. Максимально допустимую угловую скорость вращения которого найдем из равенства Fmax и [Fmax].

Приравниваем равенства (63) и (66). Тогда с учетом (62) будем иметь:

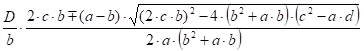
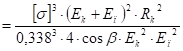
(67).

При заданных параметрах лопасти, клубня и столона выражения (67) является уравнением относительно угловой скорости вращения отбойного валика.

Сгруппируем члены при одинаковых степенях с.

Угловая скорость щ входит только в выражение с. Поэтому уравнение (68) можно рассматривать как квадратичное уравнение относительно с:

Решая его, получаем:

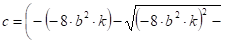
(69).

Используя выражение с из (58), найдем допустимое значение щ:

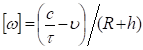
(70).

Для выбора рациональных параметров клубнеотражателя органа выносной сепарации проанализируем графики (рис. 4), полученные на основе выражения (69) и (70). При этом зададим значения следующих величин: Сб=0,01 — жесткость столона на растяжение, Н/м; =1 — скорость клубня, м/с; =0,05 — продолжительность второй фазы удара, с; D=0,05 — средний диаметр клубня, м; [у]=0,83 — нормальное напряжение в клубне, Па; Ек=2,7· 106 — модуль упругости (модуль Юнга) клубня, Н/м 2.

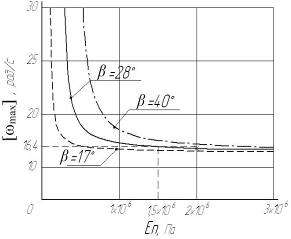
а) б)

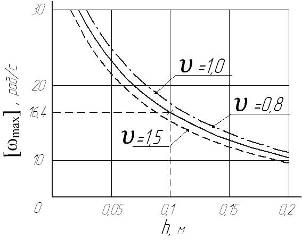
• а) от высоты лопасти при различных величинах скорости движения клубня
• б) от материала лопасти при различных величинах угла ее поворота относительно оси вращения отбойного валика

[щmax] - максимально допустимая угловая скорость лопастного отбойного валика, рад/с; в — угол поворота лопасти относительно оси вращения отбойного валика, градус; Еп — модуль упругости лопасти, Па; h — высота лопасти, м; х — скорость движения клубня, м/с.

Рисунок 4. Зависимость изменения угловой скорости вращения лопастного отбойного валика от его параметров.

Графически зависимость максимально допустимой угловой скорости вращения [щmax] лопастного отбойного валика от скорости перемещения клубня на поверхности органа выносной сепарации представлена на рисунке 4а, а зависимость [щmax] от модуля упругости материала лопасти ЕП при различных величинах угла поворота лопастей относительно своей оси в — на рисунке 4б. Поскольку на большинстве картофелеуборочных машин поступательная скорость полотна выносной сепарации не превышает 1 м/с, и, принимая рабочий зазор установки отбойного валика д=0,03 м, величину [щmax] целесообразно ограничить значением 16,4 рад/с, что соответствует частоте вращения 153 об/мин.

Принимаем максимально допустимую угловую скорость вращения лопастного отбойного валика [щmax]=16,4 рад/с, модуль упругости материала изготовления лопасти Еп=1,5· 106Па, высоту лопасти h=0,1 м, угла поворота лопасти относительно оси вращения отбойного валика в=0,5 рад (?29 град).

Библиографический список

• 1. Основные тенденции развития высокопроизводительной техники для картофелеводства / Колчин Н. Н., Бышов Н. В., Борычев С. Н. и др. — Тракторы и сельхозмашины. 2012. № 4. С. 46−51
• 2. Рембалович Г. К. Повышение эффективности функционирования и надежности сепарирующей горки картофелеуборочных машин. Автореферат диссертации на соискание ученой степени кандидата технических наук / Мордовский государственный университет им. Н. П. Огарева. Саранск, 2005
• 3. Инновационные решения уборочно-транспортных технологических процессов и технических средств в картофелеводстве /Рембалович Г. К., Бышов Н. В., Борычев С. Н. и др. — Сборник научных докладов ВИМ. 2011. Т. 2. С. 455−461.
• 4. Технологическое и теоретическое обоснование конструктивных параметров органов вторичной сепарации картофелеуборочных комбайнов для работы в тяжелых условиях/ Н. В. Бышов, С. Н. Борычев, И. А. Успенский [и др.] // Вестник РГАТУ. — 2012. — № 4(16). — С. 87−90.
• 5. Патент № 2 245 011, RU, М.кл.2 А 01 D 33/08 Устройство для отделения корнеклубнеплодов от примесей / Борычев С. Н., Рембалович Г. К., Успенский И. А. — Опубл. 12.05.2003.
• 6. Патент № 63 637, RU, М.кл.2 А 01 D 33/08 Устройство для отделения корнеклубнеплодов от примесей / Паршков А. В., Рембалович Г. К., Борычев С. Н. и др. — Опубл. 04.10.2006.
• 7. Патент № 95 960, RU, М.кл.2 А 01 D 33/08 Устройство для отделения корнеклубнеплодов от примесей / Безносюк Р. В., Бышов Д. Н., Рембалович Г. К. и др. — Опубл. 20.07.2010, бюл. № 20.
• 8. Патент № 2 454 850, RU, М.кл.2 А 01 D 33/08 Устройство для отделения корнеклубнеплодов от примесей / Павлов В. А., Рембалович Г. К., Безносюк Р. В. и др. — Опубл. 14.02.2011.

References

• 1. Osnovnye tendencii razvitija vysokoproizvoditel’noj tehniki dlja kartofelevodstva / Kolchin N.N., Byshov N.V., Borychev S.N. i dr. — Traktory i sel’hozmashiny. 2012. № 4. S. 46−51
• 2. Rembalovich G.K. Povyshenie jeffektivnosti funkcionirovanija i nadezhnosti separirujushhej gorki kartofeleuborochnyh mashin. Avtoreferat dissertacii na soiskanie uchenoj stepeni kandidata tehnicheskih nauk / Mordovskij gosudarstvennyj universitet im. N.P. Ogareva. Saransk, 2005
• 3. Innovacionnye reshenija uborochno-transportnyh tehnologicheskih processov i tehnicheskih sredstv v kartofelevodstve /Rembalovich G.K., Byshov N.V., Borychev S.N. i dr. — Sbornik nauchnyh dokladov VIM. 2011. T. 2. S. 455−461.
• 4. Tehnologicheskoe i teoreticheskoe obosnovanie konstruktivnyh parametrov organov vtorichnoj separacii kartofeleuborochnyh kombajnov dlja raboty v tjazhelyh uslovijah/ N.V. Byshov, S.N. Borychev, I.A. Uspenskij [i dr.] // Vestnik RGATU. — 2012. — № 4(16). — S. 87−90.
• 5. Patent № 2 245 011, RU, M.kl.2 A 01 D 33/08 Ustrojstvo dlja otdelenija korneklubneplodov ot primesej / Borychev S.N., Rembalovich G.K., Uspenskij I.A. — Opubl. 12.05.2003.
• 6. Patent № 63 637, RU, M.kl.2 A 01 D 33/08 Ustrojstvo dlja otdelenija korneklubneplodov ot primesej / Parshkov A.V., Rembalovich G.K., Borychev S.N. i dr. — Opubl. 04.10.2006.
• 7. Patent № 95 960, RU, M.kl.2 A 01 D 33/08 Ustrojstvo dlja otdelenija korneklubneplodov ot primesej / Beznosjuk R.V., Byshov D.N., Rembalovich G.K. i dr. — Opubl. 20.07.2010, bjul. № 20.
• 8. Patent № 2 454 850, RU, M.kl.2 A 01 D 33/08 Ustrojstvo dlja otdelenija korneklubneplodov ot primesej / Pavlov V.A., Rembalovich G.K., Beznosjuk R.V. i dr. — Opubl. 14.02.2011.