Аномально большие фотонапряжения в полупроводниковых пленках обусловленные реактивной фотоЭДС

АНОМАЛЬНО БОЛЬШИЕ ФОТОНАПРЯЖЕНИЯ В ПОЛУПРОВОДНИКОВЫХ ПЛЕНКАХ ОБУСЛОВЛЕННЫЕ РЕАКТИВНОЙ ФОТОЭДС

Фотоэдс, возникающая при освещении полупроводника, в основном объясняют разделением пар свободных носителей, возникающих при фотогенерации связанных с неоднородностью либо кристалла, либо освещения [1]. Однако, имеются другие фотогальванические эффекты обусловленные эффектом увлечения, баллистическим фототоком, реактивным фотоэдс и др [4, 5, 6]. Влияние этих эффектов на фотоэдс в тонких пленках изучено недостаточно. В настоящей работе рассмотрим влияние отражения фотоэлектронов от поверхности на фотоэдс в тонких пленках.

Пусть свет сильно поглощается в приповерхностной области полупроводника. Если энергия фотона h больше ширины запрещенной зоны E_g полупроводника, то носители генерированные за счет поглощения фотона имеют избыточную кинетическую энергию и импульс отличную по сравнению с равновесными носителями в образце. В случае, когда зона проводимости и валентная зона имеют параболический вид скорости фотоэлектронов _e и фотодырок _h в момент рождения связаны соотношением [6].

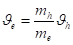
m_e и m_h массы электронов и дырок.

Энергия фотона h и скорости рождаемых электронов и дырок _{h, e} связаны с соотношением [6].

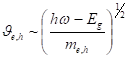
E_g — ширина запрещенной зоны.

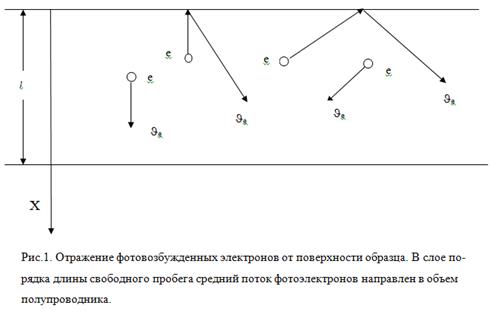
При этом половина быстрых электронов и дырок направляются в объем, а другая половина на поверхность. Носители, которые генерируются на расстоянии меньше чем длины свободного пробега, отражаются от поверхности. Носители, которые направлены в объем дают ток (где I-интенсивность света) [6], а носители направленные к поверхность отражаются от поверхности и также дают токи направленные в объем (рис.1). Таким образом, в приповерхностном слое толщиной порядка длины свободного пробега возникают потоки быстрых фотоэлектронов направленных от поверхности в объем. Токи обусловленные таким движением называются реактивными фототоками [5]. По мере удаления от поверхности электроны и дырки за счет рассеяния в объеме теряют направленные скорости. Вследствии этого ток носителей внутри образца быстро уменьшается. Толщина слоя, где отраженные носители дают вклад в реактивный фототок, составляет порядка длины свободного пробега. При примесном возбуждении монохроматическим светом возникают только электронные токи.

Оценим величину ЭДС, обусловленную носителями отраженными от поверхности. Плотность полного тока в приповерхностной области равна [6].

(1).

где, — проводимость образца, — средняя скорость возбуждаемых светом электронов, k — коэффициент поглощения, _е-время свободного пробега.

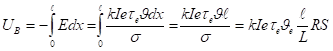
(3).

Здесь R-сопротивление образца, S-площадь поперечного сечения пленки, -длина свободного пробега электрона, L-толщина образца.

Если идет межзонная генерация, фотоэлектроны и дырки имеют свои скорости _e и _h и свои времена свободного пробега _e и _h. Тогда реактивный ток имеет следующий вид:

(4).

Полный ток опять состоит из тока проводимости и баллистического тока.

(5).

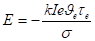
(2).

В случае слабого фотовозбуждения реактивная ЭДС отраженных электронов равна Здесь _e и _h-электронные и дырочные проводимости.

В режиме короткого замыкания E=0 и ток короткого замыкания равен баллистическому току J_кз=J_B.

В режиме холостого хода J=0 напряженность электрического поля равна.

ЭДС генерируемая в образце равна.

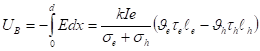
(7).

Здесь и — длины свободного пробега электронов и дырок. Таким образом, реактивная фотоэдс прямо пропорциональна интенсивности света и определяется скоростью фотоэлектронов, временами и длинами свободного пробега возбуждаемых носителей.

ЭДС отраженных носителей в чистом виде в эксперименте не наблюдается. Обычно, ЭДС отраженных носителей складывается с ЭДС Дембера и поверхностьной фотоЭДС. Поэтому, для выявления относительной роли ЭДС отраженных носителей в измеряемой ЭДС необходимо сравнить ее с ЭДС Дембера.

Для расчета ЭДС Дембера рассмотрим полупроводник n-типа и будем предполагать, что концентрация ловушек мала (n=p) и освещение не очень сильное и электропроводность при освещении мало отличается от темновой электропроводности ₀ тогда ЭДС Дембера будет равна.

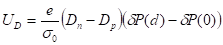
(8).

Если d больше длины диффузии L, то Р (d) << Р (0), тогда избыточная концентрация для толстой пластинки определяется следующим выражением.

.

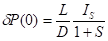
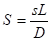
здесь — безразмерная скорость поверхностной рекомбинации, D — коэффициент амбиполярной диффузии. Поэтому окончательно получим.

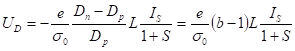
(9).

Здесь b=D_n/D_p.

Оценим отношение баллистического фотоэдс на ЭДС Дембера U_B/U_D. Для грубой оценки положим, что.

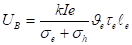
Тогда учитывая (9) для соотношения баллистического напряжения к ЭДС Дембера получим.

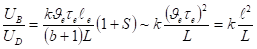
(10).

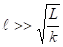
Если k² >L, то реактивная ЭДС больше ЭДС Дембера. Для этого длина свободного пробега должна быть. Таким образом, следует ожидать, что баллистическая фотоэдс может преобладать над ЭДС Дембера только в образцах с большой длиной свободного пробега при сильном поглощении света. В тонких пленках баллистическая фотоЭДС, повидемому, наблюдается вместе с другими видами фотоЭДС и при интерпретации результатов эксперимента может быть истолкована как Демберовкая ЭДС.

В некоторых косонапыленных полупроводниковых пленках при освещении светом наблюдаются фотонапряжения больше ширины запрещенной зоны полупроводника. Такие напряжения называются аномально большими фотонапряжениями (АФН-эффект). Для объяснения этого эффекта часто пользуются различными моделями [2−3]. Как известно по работам [4−6], баллистические и реактивные фототоки могут существенно влиять на фотоЭДС, генерируюмую в тонких пленках. Однако для объяснения АФН эффекта не используется влияние баллистических фототоков. Рассмотрим фотоЭДС на аномально большие фотонапряжения, генерируемые в тонких косонапыленных полупроводниковых пленках. В тонких пленках, полученных косым напылением, поверхность может иметь микрорельеф с пилаобразной зубчатой структурой, например, такой, как на рис. 2. Рассмотрим отражение фотоэлектрона от одного элемента зубчатой поверхности, размеры которого меньше длины свободного пробега фотоэлектрона. Также предположим, что свет сильно поглощается и фотоэлектроны генерируются в верхней части элемента.

Если энергия поглощаемого фотона больше ширины запрещенной зоны, то скорость фотоэлектронов может больше тепловой скорости равновесных носителей. При генерации носителей в указанной части элемента любой электрон после нескольких отражений от поверхности будет вылетать преимущественно в направлении биссектрисы угла [7] (рис. 2 а). Пусть ось ОО` с нормалью плоскости подложки составляет угол. Тогда скорость фотоэлектронов, вылетающих из зубчатой поверхности, должна быть направлена примущественно по биссектрисе зубчатого элемента (рис. 2, а). Таким образом, на указанном участке фотоэлектроны всегда будут вылетать со скоростью, направленной вдоль оси ОО`, независимо от вида функции распределения скоростей рожденных фотоэлектронов.

Рассматривая пленку в целом, можно считать, что при освещение сверху фотоэлектроны отлетают от верхней поверхности под углом относительно нормали (рис. 2, б). На глубине порядка длины свободного пробега эти фотоэлектроны теряют свои импульсы и направленная скорость хаотизируется. В приповерхностном слое порядка длины свободного пробега существует баллистический ток фотоэлектронов, генерированный на зубчатой поверхности образца. Х-составляющая этого баллистического тока, параллельная плоскости подложки, равна.

(11).

Нормальная к поверхности составляющая баллистического фототока имеет вид.

(12).

Плотность полного тока равна.

(13).

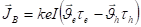
где; -проводимость образца; Е-напряженность электрического поля.

Полный ток в образце равен.

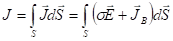
(14).

Рассмотрим распределение электрического поля и плотности тока внутри образца. Из уравнения Максвелла rotE=0 получим.

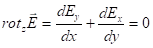
(15).

Длина пленки всегда достаточно велика по сравнению с ее толщиной, и Е_у не зависет от х: dE_y/dx=0; тогда из (5) следует.

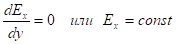
(16).

Отсюда можно сделать вывод, что для длинных образцов продольная составляющая электрического поля не зависит от y.

Внутри длинного образца усоставляющая тока равна нулю.

(17).

Отсюда.

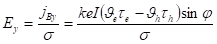
(18).

Это поле направлено перпендикулярно к поверхности образца и отлично от нуля только в слое толщиной порядка длины свободного пробега и приводит к реактивной ЭДС, предсказанной В. И. Белиничером и С. М. Рывкином [5]. Проанализируем распределение токов. Для длинной пластинки плотность тока j_y равна нулю. В режиме короткого замыкания Е_х=0 и плотность тока определяется только баллистическим током и равна.

(19).

В режиме холостого хода добавляется еще полевой ток и плотность тока вдоль оси х равна.

(20).

Следует подчеркнуть, что направление полевого тока и баллистического тока противоположны. Так как Е_х не зависит от у, а j_xB(y) затухает при увеличение у, то вблизи освещенной поверхности преобладает баллистический ток, а в глубине полевой ток и направления плотности токов становятся противоположными. Вследствии этого в образце возникают вихревые токи (рис.3). При этом пластинка приобретает магнитный момент, который можно обнаружить экспериментально подобно фотомагнитному эффекту [1].

Вычислим величину напряжения поперечного баллистического эффекта. ЭДС и ток короткого замыкания связаны соотношением.

(21).

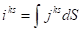
Здесь — ток короткого замыкания, R — полное сопротивление образца. При слабом освещении.

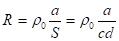
(22).

где ₀ — удельное сопротивление, а — длина, Sплощадь поперечного сечения образца. Оценим ток короткого замыкания фотоноситель отражение пленка микрорельеф.

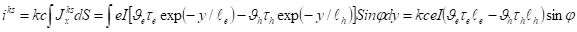
(23).

Здесь и длины свободного пробега электронов и дырок.

Подставляя (22) и (23) в (21), получим следующее выражение:

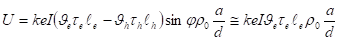
(24).

которое позволяет оценить величину АФН эффекта. Величина ЭДС достаточно велика. Примем для оценки I10²¹(м²с)^-1; _ее10^-7м; ₀ =10³ Ом^.м; ~ 10¹; a/d~10⁴, тогда для ЭДС, генерируемой в пленке, получим U10³ В.

ЭДС такой величины в высокоомных косонапленных пленках считается аномально большой. Таким образом, реактивная фотоЭДС фотоэлектронов, отраженных от поверхности с косым зубчатым микрорельефом, может давать аномально большие фотонапряжения.

В низкоомных и толстых образцах ЭДС шунтируется проводимостью слоя и поэтому АФН эффект может не наблюдаться, а в тонких (порядка длины свободного пробега) и высокоомных (₀10 Ом^.м) пленках она принимает достаточно большие значения и наряду с существующими механизмами может объяснит аномально большие значения фотоЭДС.

[1]. В.Л.Бонч-Бруевич, С. Г. Калашников. «Физика полупроводников» (М., Наука, 1977), с. 672.

[2]. Э. И. Адирович, Т. Мирзамахмудов, В. И. Рубинов, Ю. М. Юабоков, ФТТ, 7, 3665 (1965).

[3]. К. Као, В.Хуанг. Перенос электронов в твердых телах (М., Мир, 1984), ч.2, с. 368 [Пер. с англ.: K. C. Kao, W. Hwang. Electrical transport in solids (Oxford-New York-Toronto-Sydney-Paris-Frankfurt., Pergamon Press, 1981) v.2 ].

[4]. А. В. Саченко, О. В. Снитко. Фотоэффекты в приповерхностных слоях полупроводников (Киев, Наука думка, 1984), с. 32.

[5]. В. И. Белиничер, С. М. Рывкин. Реактивная фотоэлектродвижущая сила в полупроводника. ЖЭТФ, 1, с.353−360 (1981).

[6]. Е. Л. Ивченко, Г. Е. Пикус. Фотогальванические эффекты в полупроводниках. В.сб.: Проблемы современной физики. (Л., Наука, 1980), с.275−293.

[7]. Г. А. Гальперин, А. Н. Земляков. Математические биллиарды. (М., Наука, 1990).