2D течение в прямоугольной полости

Рассмотрим двумерное стационарное течение в прямоугольной полости — рис. 2. Поле скорости в этом случае имеет две компоненты. На верхней границе поставим условия:

(22).

На остальных границах полости выполняется условие прилипания .

На рис. 2−3 представлены данные моделирования течения в прямоугольной полости при числе Рейнольдса соответственно.

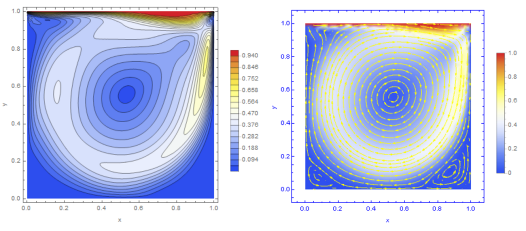
Рис. 2. Ламинарное течение в прямоугольной полости при числе Рейнольдса: слева — линии уровня модуля скорости; справа — линии тока

Полученные данные при согласуются с известными результатами [20]. Однако уже при обсуждаемый метод решения задачи о течении в прямоугольной полости теряет устойчивость, что, видимо, указывает на отсутствие стационарных решений в этой области параметров. Из данных, приведенных на рис. 3 можно видеть, что вторичные течения развиваются в углах полости. Было установлено в экспериментах с водой и раствором глицерина [21], что переход к режиму автоколебаний в кубической полости происходит при. Течение в полости в экспериментах [21] возбуждалось движением ленты транспортера, прилегающей к верхней грани. Таким образом, с большой точностью выполнялись граничные условия (22) для скорости.

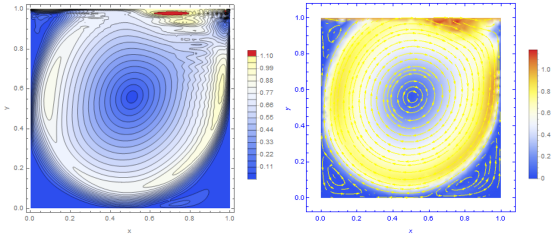
Рис. 3. Ламинарное течение в прямоугольной полости при числе Рейнольдса: слева — линии уровня модуля скорости; справа — линии тока

С другой стороны, некоторые численные модели в плоском случае демонстрируют устойчивость вплоть до [20]. Заметим, что наши результаты получены на сетках. Кроме того, мы использовали уравнения Навье-Стокса в исходной форме, тогда как, например, в [20] численно интегрировалась система уравнений для функции тока и завихренности, т. е. поле скорости предполагалось заведомо более гладким, чем в обсуждаемой задаче (19) и (22).