Расчет эволюции возмущений свободной поверхности при помощи метода конечных элементов для различных вариантов уравнений мелкой воды

Расчет эволюции возмущений свободной поверхности при помощи метода конечных элементов для различных вариантов уравнений мелкой воды

Одна из простейших моделей геофизической гидродинамики — уравнения мелкой воды, достаточно хорошо описывают атмосферные и океанические течения во вращающихся областях. Всевозможные асимптотические варианты таких уравнений, в частности, приближение бета-плоскости, сравнительно полно исследованы аналитическими и численными методами. При использовании численных методов чаще всего применяются специальные конечно-разностные схемы, предотвращающие влияние сеточной вязкости и других паразитных эффектов.

Целью настоящей работы является демонстрация эффективности применения метода конечных элементов (МКЭ). Показано, что уже простейшие варианты полунеявных временных схем МКЭ позволяют строить решения для локализованных начальных возмущений свободной поверхности во вращающейся жидкости. Привлекательность использования МКЭ, в частности, обусловлено тем, что для построения решения в областях со сложными границами (озера, внутренние моря и т. п.) не требуется конструирования сложных сеточных схем, легко реализуются различные краевые условия, гладкость решения не имеет существенного значения, и без труда учитываются различные физические нелинейности.

Программная реализация МКЭ осуществлялась при помощи пакета FreeFem++, предназначенного для численного решения широкого класса задач математической физики.

Уравнения мелкой воды на произвольной поверхности Уравнения мелкой воды хорошо известны и в безразмерных переменных имеют вид:

.

.

.

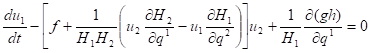
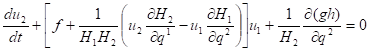
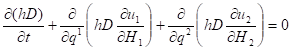
Здесь — скорость, — возвышение свободной поверхности, , — криволинейные координаты, — ускорение силы тяжести и — коэффициенты Ламе, , — функция Кориолиса.

Приведенные уравнения справедливы для произвольной достаточно гладкой поверхности, что позволяет использовать их при описании сложных рельефов, в частности, учитывать, что поверхность Земли является геоидом.

В простейшем случае плоской поверхности (классический вариант уравнений мелкой воды) имеем (,, = = 1, ,):

, ,.

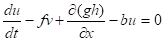
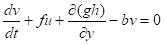
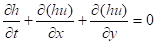
где функция Кориолиса аппроксимирована либо константой (- плоскость), либо линейной функцией (бета-плоскость); - коэффициент вязкого сопротивления.

Основным объектом исследования в работе являются уравнения в приближении бета-плоскости, которые записываются в форме:

.

.

.

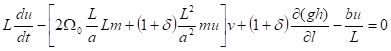
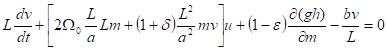
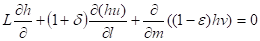
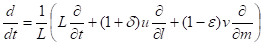
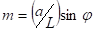
Здесь использованы безразмерные координаты, , связанные с долготой и широтой: и, где — характерный масштаб движений, — радиус сферы,, .- угловая скорость вращения.

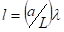
В случае имеем малый параметр и вспомогательные малые функции:

.

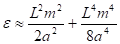
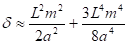
Численная реализация МКЭ.

Приведем схему реализации МКЭ, используя для сокращения выражений уравнения мелкой воды на плоскости. На интервале времени зададим, где — шаг по времени. Введем обозначения, ,,. Для аппроксимации производных по времени используем полунеявные схемы:

.

.

.

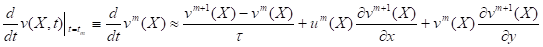
Тогда полунеявная аппроксимация уравнений имеет вид:

.

.

.

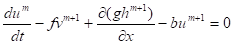
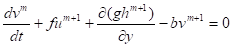
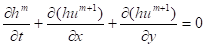
уравнение гидродинамика аппроксимация Для применения МКЭ используем слабую формулировку задачи, которая получена умножением уравнений на тестовые функции, , с последующим интегрированием по области, применением формулы интегрирования по частям и учетом краевых условия на границе.

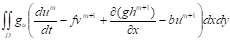
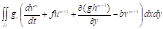
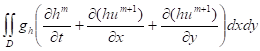
+ + =0.

Здесь для простоты предполагается, что заданные краевые условия приводят к исчезновению интегралов по границе области .

Вычислительный эксперимент.

Основная цель вычислительного эксперимента — сравнение результатов решения задачи для различных моделей мелкой воды. В качестве начальных данных:

,.

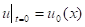
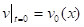
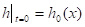
в частности, выбиралось вращательное течение с дрейфом центра вращения и локализованным возмущением свободной поверхности типа «горб» — «яма»:

,.

,.

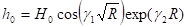
где, , задают интенсивность и дрейф вращения с центром в точке, параметры, , характеризуют возмущение свободной поверхности и степень локализации.

Вычисления проводились в окрестности точки с координатами с характерным размером области для параметров, ,. Для расчетов использовались кусочно-квадратичные конечные элементы и триангуляция области с характерным относительным размером треугольников 0.005. Компьютерный эксперимент показал, что предложенная схема аппроксимации и МКЭ позволяют проводить расчеты на достаточно большом интервале времени порядка с относительной погрешностью. При использовании быстрых алгоритмов решения систем линейных уравнений, требующихся для численной реализации МКЭ, скорость вычислений существенно увеличивается.

Для указанных начальных данных с течением времени происходит разрушение начального возмущения свободной поверхности. В среднем для всех моделей получаются примерно одинаковые сценарии эволюции течения и возмущения свободной поверхности. Регулярная структура возмущения сохраняется на интервале времени и начинает достаточно быстро разрушаться при. Для неподвижного центра вращения (,) времени сохранения регулярной структуры увеличивается Параметры, ,, варьировались в окрестности значений, ,, и их изменения (примерно на 100 процентов) слабо влияют на эволюцию структуры возмущения. Выбор для проведения расчетов различных моделей оказывает существенное влияние лишь на этапах эволюции при. Например, разрушение возмущения свободной поверхности в случае использования модели для касательной плоскости или модели для бета-плоскости происходит примерно в два раза медленнее, чем в случае использования модели для сферы, что естественно связано с учетом кривизны поверхности. В заключение приведем рисунок, демонстрирующий распад начального возмущения для модели бета-плоскости.

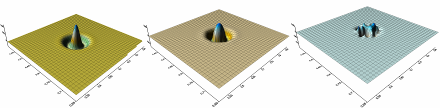
Рис. 1. Поверхность для моментов, ,

Анализ результатов показывает, что все три модели, описывающие поведение мелкой воды, с начальным распределением, соответствующим вихревому течению и локализованному возмущению свободной поверхности, на сравнительно малых интервалах времени демонстрируют примерно одинаковое поведение. Различие моделей сказывается лишь на эволюцию структуры возмущений для больших времен. МКЭ успешно применим к рассмотренному классу задач и позволяет проводить стабильные вычисления на достаточно большом интервале времени. Метод позволяет эффективно предотвратить паразитные дисперсионные эффекты и эффекты сеточной вязкости.