Коэффициенты сжатия, скорости и расхода при истечении через незатопленное малое отверстие

Для вычисления площади, скорости и расхода струи необходимо знать коэффициенты истечения и. Значения этих коэффициентов могут зависеть от нескольких факторов: формы и кромки отверстия, режима движения жидкости, поверхностного натяжения, а также от положения отверстия относительно стенок резервуара. Значение коэффициента сжатия для данного отверстия зависит от степени сжатия струи.

Полное сжатие характеризуется тем, что струя вытекающей жидкости испытывает сжатие по всему периметру отверстия.

Неполное сжатие происходит в тех случаях, когда струя подвергается сжатию только на некоторой части периметра. Это может наблюдаться, например, когда отверстие в вертикальной или наклонной стенке резервуара примыкает непосредственно к дну (отсутствует сжатие по одной из сторон) или отверстие примыкает к дну и расположено в углу резервуара (отсутствует сжатие по двум сторонам),.

При расположении отверстия в дне сосуда также может наблюдаться неполное сжатие. И в этом случае вдоль стенки (или стенок) резервуара, вплотную к которым примыкает отверстие, траектории частиц жидкости будут прямолинейными.

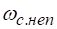
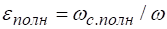
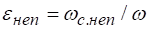
В связи с этим при одинаковой площади отверстия и прочих равных условиях площадь сечения, сжатого на некоторой части периметра, больше, чем площадь сечения, сжатого по всему периметру,. Отсюда получается, что при неполном сжатии коэффициент сжатия больше, чем при полном сжатии (для одинаковых прочих условий истечения).

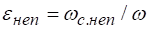
При полном сжатии различают совершенное и несовершенное сжатие.

Совершенное сжатие характеризуется наибольшей кривизной траекторий крайних струек вытекающей струи и соответственно максимальным сжатием струи. Для получения совершенного сжатия струи отверстие должно быть достаточно удалено от боковых стенок и дна сосуда, а также от свободной поверхности.

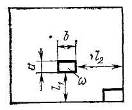
Рис. 3.

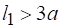
Сжатие будет совершенным, если расстояния от любой грани отверстия (рис. 3) до стенок и дна резервуара (сосуда) будут больше, чем утроенный соответствующий поперечный размер отверстия, т. е. при и .

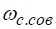
Несовершенное сжатие наблюдается при болей близком, чем указано, расположении отверстия к направляющим поток стенкам резервуара.

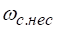
При несовершенном сжатии кривизна траекторий частиц вблизи отверстия меньше, чем при совершенном сжатии. В связи с этим сжатие по соответствующей стороне (близко расположенной к направляющей поток стенке или дну) уменьшается. Следовательно, площадь сжатого сечения при несовершенном сжатии и прочих равных условиях (в том числе и равной площади отверстия) больше, чем при совершенном сжатии. Естественно, коэффициент при несовершенном сжатии больше, чем при совершенном сжатии.

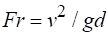
Итак, неполнота или несовершенство сжатия приводит к увеличению коэффициентов сжатия.

В условиях совершенного сжатия процесс истечения происходит под действием сил тяжести, вязкости и поверхностного натяжения, которые отражены соответственно (для круглого отверстия диаметром):

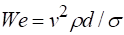
числом Фруда ;

числом Рейнольдса ;

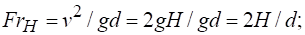
числом Вебера .

Влияние поверхностного натяжения наглядно демонстрируют опыты, в которых вблизи вытекающей в атмосферу струи воды устанавливали открытый сосуд с эфиром. Эфир испарялся, поверхностное натяжение на поверхности струи уменьшалось, коэффициент сжатия струи заметно увеличивался, соответственно расход также увеличивался.

А.Д. Альтшулем предложены следующие выражения для чисел Fr, Re и We:

;

.

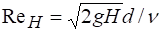
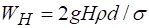
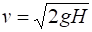
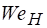
т. е. в принято =1 и, следовательно, .

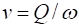
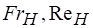
Такой вид выражений для и удобнее, так как в них входят только известные величины и не входит расход, неизвестный до выполнения расчетов (в Fr, Re и We входит). Коэффициенты расхода, скорости и сжатия в общем случае для отверстия с острой кромкой являются функциями чисел Рейнольдса, Фруда и Вебера.

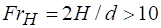
Многочисленные экспериментальные исследования истечения через отверстия различных жидкостей позволили А. Д. Альтшулю установить, что коэффициенты расхода при истечении через незатопленные круглые малые отверстия практически не зависят от влияния сил тяжести и поверхностного натяжения (т. е. наступает область, практически автомодельная относительно чисел Fr и We) при соблюдении условий.

.

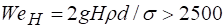
т. е. при, и.

.

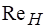
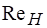
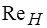
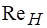
Полученные зависимости и при совершенном сжатии от представлены на рис. 4. Как видно, с увеличением до 10⁵ коэффициент скорости растет, при дальнейшем увеличении значения могут считаться постоянными и равными = 0,97.

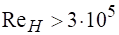
Коэффициент сжатия с ростом уменьшается, а при >10⁵ коэффициент также может считаться постоянным и приниматься равным для совершенного сжатия 0,61−0,64.

Зависимость от достаточно сложная. Вначале при небольших значениях коэффициент растет, достигает максимума, а затем уменьшается, приближаясь при больших к постоянному значению, приблизительно равному 0,6.

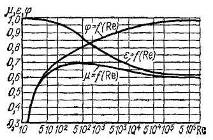
Рис. 4.

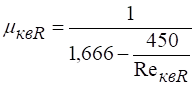
При >10⁵ можно считать, что для круглого отверстия не зависит от (наступает автомодельная область относительно). Точнее, перестает зависеть от при. В этих условиях .

Коэффициенты расхода для малых квадратных и прямоугольных отверстий несколько отличаются от для круглых отверстий.

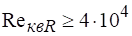
Коэффициенты расхода квадратных отверстий при могут быть найдены по формуле Ю. А Скобельцына, полученной в результате обработки опытных данных,.

.

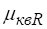
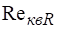
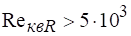
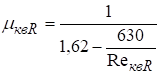
При коэффициент практически не зависит от и равен 0,6.

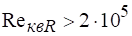
Коэффициенты расхода прямоугольных отверстий при определяются также по эмпирической формуле Ю. А. Скобельцына.

.

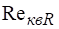
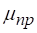
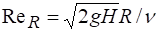
При наступает автомодельность и перестает зависеть от, в этих условиях =0,62.

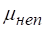
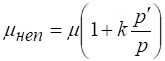
Следует обратить внимание на то, что в некоторых приведенных формулах число Рейнольдса определено по гидравлическому радиусу отверстия .

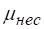
Неполное и несовершенное сжатие. При неполном сжатии коэффициент расхода больше, чем при полном сжатии. Это увеличение отражено в эмпирической формуле, по которой определяется при больших значениях Re:

.

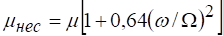
где — коэффициент расхода при полном сжатии; - периметр всего отверстия; - длина той части периметра, на которой сжатие отсутствует; - коэффициент, равный 0,13 для круглых и 0,15 для прямоугольных отверстий.

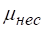
При полном, но несовершенном сжатии коэффициент расхода также больше, чем коэффициент расхода при совершенном сжатии и определяется по эмпирической формуле.

.

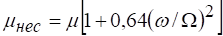
где и — площади соответственно отверстия и стенки, в которой выполнено отверстие.