Резонанс в цепях несинусоидального тока

Рассмотрим, как изменяются ток и напряжение в перестриваемом резонансном контуре. Для решения этой задачи применим принцип наложения. Определим резонансные частоты на каждой гармонике в отдельности, а затем проведем суммирование действующих значений токов и напряжений по известной формуле (10). При вычислении показания амперметра действующие значения гармонических составляющих тока записывались… Читать ещё >
Резонанс в цепях несинусоидального тока (реферат, курсовая, диплом, контрольная)
В цепях несинусоидального тока проявление резонансных свойств чаще всего наблюдается при изменении реактивного параметра в резонансном контуре, либо при совпадении резонансных частот цепи с частотами той или иной гармоники ЭДС или тока источника.
Рассмотрим, как изменяются ток и напряжение в перестриваемом резонансном контуре. Для решения этой задачи применим принцип наложения. Определим резонансные частоты на каждой гармонике в отдельности, а затем проведем суммирование действующих значений токов и напряжений по известной формуле (10).
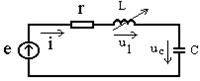
Рис. 4.
Проведем анализ резонансных характеристик перестраиваемого последовательного резонансного контура, подключенного к источнику несинусоидальной ЭДС. На рис. 4.
представлена схема последовательного резонансного контура с переменной индуктивностью. Здесь ЭДС.
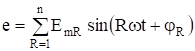
гармонический состав ЭДС фиксирован, сопротивление r и емкость С постоянны, индуктивность.
L изменяется от О до . Определить зависимость действующих значении тока I и напряжений на конденсаторе и на катушке от величины индуктивности L.
При воздействии одной R-й гармоники действующее значение тока определяется по закону Ома.


Здесь индуктивное и емкостное сопротивления R-й гармонике.

резонансный ток R-й гармоники.

Действующие значения напряжения на конденсаторе и на катушке.

.
При воздействии несинусоидальной ЭДС.
Действующие значения тока и напряжений на конденсаторе и катушке.

(21).
(22).


(23).
При изменении индуктивности цепь последовательно проходит режимы резонанса на каждой из гармоник. Режимам резонанса соответствует значение индуктивности, определяемое соотношением.

или.
откуда.

(24).

Рис. 5.
Проведем теперь качественное построение резонансных кривых тока I и напряжений.
Выполняя построение, положим для определенности, что ЭДС Тогда.
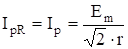
Резонансные кривые изображены на рис. 5.
Рассмотрим характерные точки этих кривых по уравнениям (21), (22), (23).
При нулевой индуктивности контура ток.

Аналогично, напряжение на конденсаторе.
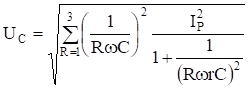
Напряжение на катушке .
Рассмотрим теперь резонансные режимы. Резонансу на R-й гармонике соответствует индуктивность (24):
—на nepвой гармонике.

- —на второй гармонике
- —и на третьей
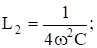

Таким образом, при увелнчении индуктивности от 0 до в нашем случае цепь проходит сначала резонанс на 3-гармонике, затем на 2-й и на 1-й.
Действующие значения тока при резонансах больше, чем (21), ввиду того, что к резонансному току данной гармоники прибавляются токи других гармоник (нерезонансные).
Резонансные напряжения увеличиваются с увеличением индуктивности, поскольку различны частоты резонирующих гармоник. При минимальной резонансной индуктивности происходит резонанс на третьей гармонике, резонансное напряжение.
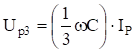
при индуктивности резонанс па второй гармонике, резонансное напряжение.
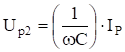
и при резонанс на первой гармонике.
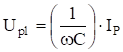
следовательно,.
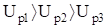
Действующие значения напряжений при резонансных индуктивностях, нельзя считать равными друг другу, поскольку резонанс напряжений имеет место толькона.
R-й гармонике (R=3, 2, 1), а действующие значения определяются всеми гармоническими составляющими напряжений (22), (23). Сдвиг максимальных значений напряжений на катушке и на конденсаторе объяснен в главе «Резонанс в электрических цепях».
При неограниченном увеличении индуктивности ток и падение на конденсаторе стремятся к нулю, а напряжение на катушке стремится к действующему значению ЭДС. Более подробный анализ может быть проведен численным методом.
Рассмотрим теперь случаи совпадения резонансных частот цепи (или отдельных ветвей) с частотами отдельных гармонических составляющих ЭДС или тока источника. Такие случаи целесообразно проиллюстрировать на примере.

рис. 6.
Пример 9. В схеме рис. 6 дано.

Определить мгновенное значение тока i и найти показания приборов I, U, P (амперметр и вольтмеир электромагнитной системы).
Решение Расчет проводится для каждой из гармонических составляющих ЭДС в отдельности.
При действии постоянной составляющей ЭДС ток в цепи отсутствует, поскольку конденсатор Ci, постоянного тока не пропускает. Поэтому На первой гармонике сопротивления реактивных элементов.
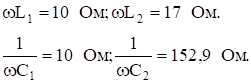
В ветви — резонанс напряжении.
Сопротивление контура.
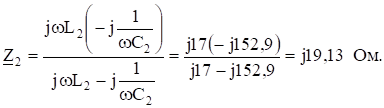
Входное сопротивление цепи Комплексная амплитуда тока.


Первая гармоника тока.

Действующее значение первой гармоники напряжения вольтметра.

активная мощность первой гармоники.
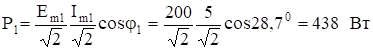
На третьей гармонике сопротивления реактивных элементов.

В контуре резонанс токов, следовательно, третья гармоника тока равна нулю Следовательно, мощность равна нулю, а напряжение на резонансном контуре равно третьей гармонике ЭДС.

На пятой гармонике сопротивления реактивных элементов.

Входное сопротивление цепи Таким образом,.
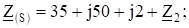
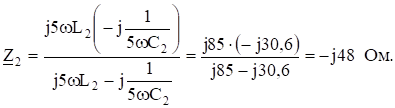

На пятой гармонике в цепи резонанс напряжений: суммарное реактивное сопротивление равно нулю.
Комплексная амплитуда пятой гармоники тока.
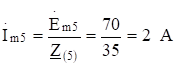
мгновенное значение.

Напряжение вольтметра.

мощность пятой гармоники.
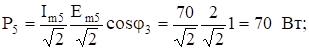
Мгновенное значение тока.
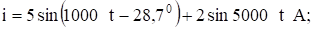
показание амперметра (амперметр электромагнитной системы показывает действующее значение тока).

Показание вольтметра (действующее значение напряжения) ,.

показание ваттметра.

Примечания:
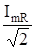
- 1).при вычислении показания амперметра действующие значения гармонических составляющих тока записывались как, где — амплитуда R-й гармоники. При опреде-лении показания вольтметра взяты действующие значения гармонических составляющих напряжения, вычисленные в тексте;
- 2) ваттметр показывает активную мощность, рассеиваемую в резисторе r, она определяется так:

что соответствует вычисленному показанию ваттметра.