Оценка показателей надёжности по результатам наблюдения за количеством отказов (биномиальный план наблюдения)

Среди всех изученных планов наблюдений особое место занимает биномиальный план (иначе схема) наблюдений. Появление этого плана связано с тем, что среди серийно выпускаемых промышленных объектов (или их элементов) встречаются такие, для которых невозможно по условиям эксплуатации регистрировать наработку с момента установки или после очередного ремонта. Это могут быть, например, насосы, подающие жидкость в резервуар, уровень в котором поддерживается системой автоматики, а расход зависит от количества включившихся в данный момент потребителей. Очевидно, что нет необходимости подсчитывать время работы насоса, суммируя наработку при каждом включении. Такая же картина наблюдается с промышленными вентиляторами или, например, с автоматизированными котлоагрегатами, подающими насыщенный пар в систему обогрева промышленных объектов.

Для расчёта показателей надёжности подобных объектов, для которых не учитывается общая наработка, а важен только факт нахождения их в одном из двух состояний, предложен биномиальный план наблюдений.

В основе биномиального плана лежат следующие допущения биномиальной схемы Бернулли.

• 1. Наблюдения ведутся за определённым фиксированным множеством объектов N, причём для каждого их них известна и одинакова вероятность безотказной работы.
• 2. Каждый объект может находиться только в одном из двух состояний:

работоспособном или противоположном — состоянии отказа. Состояние каждого объекта не зависит от состояния другого.

Результатом наблюдения при биномиальном плане является число отказов l.

Вероятность того, что при наблюдении за N объектами по биномиальному плану случайная величина l, равная числу возникающих отказов, не превысит фиксированное число x, называется функцией биномиального распределения с параметрами N и P. Она находится из выражения биномиальный котлоагрегат обогрев.

. (1).

Для того, чтобы воспользоваться уравнением (1), необходимо знать вероятность безотказной работы P. Во многих случаях эту вероятность приходится оценивать (определять приближённо) на основании результатов наблюдений за эксплуатацией.

Различают точечную и интервальную оценки вероятности безотказной работы. Точечная оценка неизвестной вероятности P может быть найдена из выражения.

(2).

где l число отказов при наблюдении за N объектами.

Эта оценка имеет ряд важных положительных статистических свойств. Она обладает свойствами несмещённости, состоятельности и минимальности границ дисперсии. Несмотря на это, оценка (2) имеет определённые недостатки. Прежде всего, величина примерно с одинаковой вероятностью может оказаться как больше, так и меньше неизвестной вероятности P. На практике желательно иметь гарантированные оценки и, для которых и .

Эти неравенства должны выполняться с заранее принятой и достаточно большой доверительной вероятностью. При этом неизвестная вероятность Р должна принадлежать интервалу с вероятностью большей или равной, чем величина, если >0.5. Случайный интервал (см. рис.1) называют — доверительным интервалом для Р, а его границы и называются — нижней и — верхней границами для параметра Р биномиального распределения, а также интервальными оценками для Р.

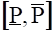
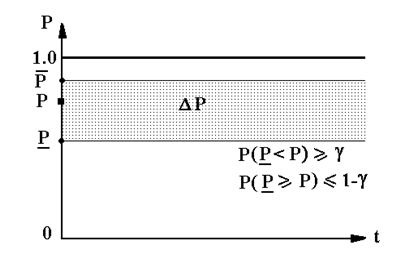
Рис. 1. Гарантированная оценки и для вероятности безотказной работы Р Р — -доверительный интервал

При расчетах обычно принимают доверительную вероятность в пределах = 0.80 — 0.99. Доверительные границы и находят по опытным данным, путём решения уравнений.

(3).

где l — число отказов.

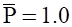
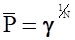
В частном случае, когда число отказов равно нулю, т. е. l = 0, значения доверительных — границ следующие,. Кроме того, при l = 1 верхняя доверительная граница равна .

Уравнения (3) представлены в неявном виде относительно неизвестных доверительных границ, что затрудняет их решение. Некоторое представление о поведении искомых переменных в зависимости от доверительной вероятности и числа отказов можно получить по рис. 2.

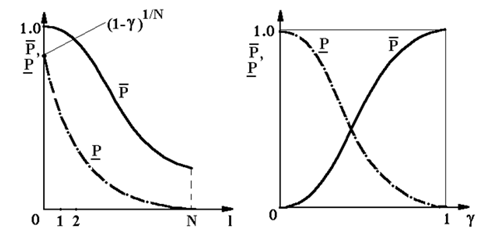
Рис. 2. Зависимости доверительных границ от значения параметров (Функции Клоппера — Пирсона)

На рис. 2 видно, что при увеличении доверительной вероятности верхняя и нижняя границы стремятся к предельным значениям, соответственно к единице и к нулю. Это соответствует смыслу понятия гарантированной оценки неизвестной вероятности.

Уравнения (3) удобно решать с использованием приближённых зависимостей.

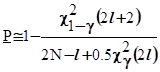
(4).

(5).

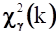
где — квантиль распределения с k степенями свободы уровня .

Таблицы распределения приведены во многих справочниках и имеются во всех современных интегрированных математических пакетах и табличных редакторах для персональных компьютеров, например, Mathcad, Matlab, Statistica, Excel и др.

Хорошие, но несколько завышенные результаты даёт следующая приближённая формула, не требующая использования специальных таблиц:

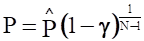
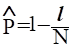
. (6).

По результатам наблюдения за N =10 однотипными насосами ТЭЦ зафиксирован l = 1 отказ.

Требуется найти приближённое значение вероятности безотказной работы Р, а также значения — границ при заданной доверительной вероятности = 0.90 .

Решение:

По приближённой формуле (4.6) получаем.

. .

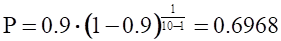
2. По приближённым уравнениям.

;

.

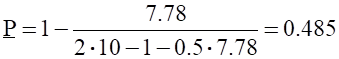
где ;

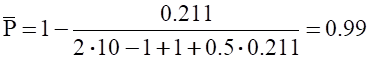
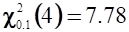
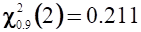
Ответ. Вероятность безотказной работы для группы из десяти однотипных насосов приближённо равна Р 0.7. С вероятностью ' 0.80 точное значение вероятности находится в пределах от 0.49 до 0.99.

Более точное значение вероятности безотказной работы и других показателей надёжности можно получить для объектов, для которых во время эксплуатации измеряется наработка до отказа и (или) между отказами.