Общие сведения. 
Регулирование скорости двигателя постоянного тока

На рисунке показана упрощённая схема автоматического регулирования скорости вращения двигателя постоянного тока с независимым возбуждением.

С якорем двигателя жестко связан маленький генератор постоянного тока с постоянными магнитами, так называемый тахогенератор. Электродвижущая сила, развиваемая якорем.

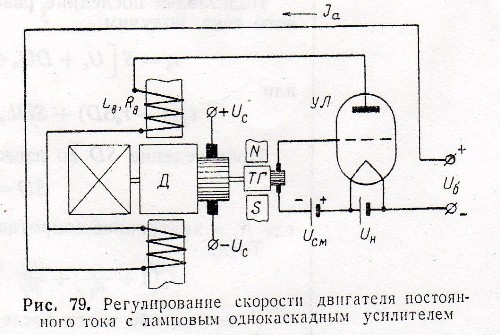
Тахогенератора, в очень широком диапазоне скоростей пропорциональна скорости вращения вала.

Напряжение, снимаемое со щёток тахогенератора, подведено к цепи сетки усилительной лампы УЛ.

В анодную цепь усилительной лампы включена обмотка возбуждения двигателя.

На рисунке 80 показана статистическая вольт — амперная характеристика лампы.

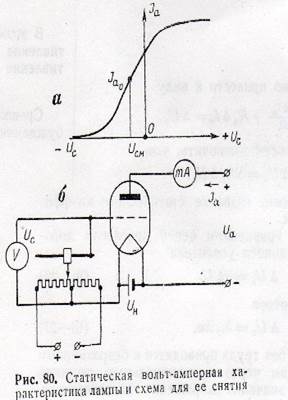
Эта характеристика снимается для ненагруженной лампы, т. е. лампы, не имеющей сопротивления анодной цепи (рис. 80 б) характеристика даёт зависимость силы анодного тока от напряжения, подведённого к сетке лампы Uc при заданном постоянном анодном напряжении.

Для того чтобы «запереть» лампу, т. е. сделать равным нулю анодный ток, к сетке необходимо подвести некоторое отрицательное напряжение, как это видно из характеристики.

Средняя часть характеристики представляет собой отрезок прямой линии. Часто подбирают режим работы лампы так, чтобы при некоторой средней нагрузке (около 50% полной) мы находились на средней части прямоугольного участка характеристики (тока Iao).

Для того чтобы попасть в эту точку, к сетке лампы должно быть приложено некоторое напряжение Ucм0 (обычно отрицательное), определяемое из характеристики лампы. Тахогенератор может развивать при этом иное напряжение; чтобы подвести к сетке то напряжение, которое нужно, в цепь сетки вводят дополнительно постоянное напряжение смещения Uсм (рис. 79).

Для малых отклонений отрезок характеристики можно заменить прямолинейным отрезком. Уравнение этого прямолинейного отрезка имеет вид.

Ia = S (Uc +DUa) *.

Где Ia — анодный ток лампы в миллиамперах;

Ua — анодное напряжение в вольтах;

c — напряжение на сетке в вольтах;

S — Статическая крутизна лампы в ма/в;

D — «Проницаемость» лампы.

В том случае, если в анодную цепь включена нагрузка, напряжение Ua не равно напряжению источника Uб, питающего анодную цепь в схеме 79 состоит из сопротивления rв и индуктивности Lв обмотки возбуждений, а анодный ток равен току возбуждения Iв. Поэтому.

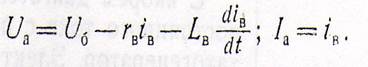
Подставляя последние равенства в управление для анодного тока, получим.

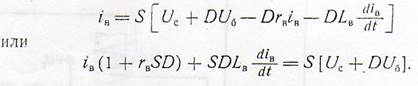
автоматический управление электродвигатель ток Произведение SD по известному уравнению лампы равно.

SD = 1/Ri,.

Где Ri — внутреннее сопротивление лампы.

Тогда.

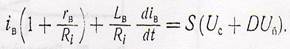
Умножим обе части последнего равенства на Ri.

Тогда.

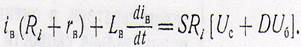
Выразим iв и Uс через приращения.

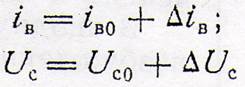
И вычтем из равенства, которое получится после подстановки отклонений, уравнение статики:

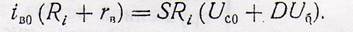
Тогда получим уравнение в отклонениях:

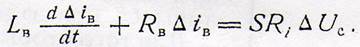
В этом уравнении через Rв обозначено полное сопротивление цепи, включая и внутреннее сопротивление лампы.

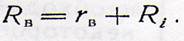
Сравним последнее уравнение с уравнением цепи возбуждения двигателя, полученным выше,.

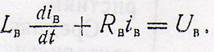
Это уравнение можно привести к виду.

Из сравнения мы можем заключить, что.

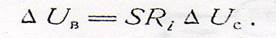
Величина Sri = (мю) носит название статического коэффициента усиления лампы.

Таким образом, к управлениям цепей двигателя добавляется лампового усилителя.

Уравнение тахогенератора.

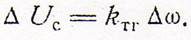
Оба эти отклонения без труда приводятся к безразмерным отклонениям. Обозначим через (омега) н номинальную скорость двигателя, через Ucн — значение напряжение тахогенератора, Соответствующее номинальному числу оборотов, и введём относительные отклонения.

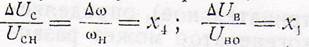
(для Х1 и Х4 сохранены обозначения, введённые выше). Тогда получаем уравнение усилителя в виде.

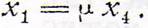
Ламповый усилитель, о котором мы говорили, можно рассматривать как жесткую связь, не вносящую лишней степени свободы в схему. Его назначение состоит в увеличении эффекта действия измерительного органа. В выражении для постоянной времени.

T = Lв/rв + Ri.

Входит внутреннее сопротивление лампы Ri, вследствие чего ламповый усилитель как бы снижает постоянную времени цепи возбуждения, за счёт увеличения сопротивления цепи.

Рассмотрим уравнение цепи возбуждения двигателя:

Lв iв + Rв iв = Uв.

L в p iв + R iв = Uв.

(L в p + Rв)iв = Uв.

W = iв/Uв = 1/Lв P + Rв =.

= = =.

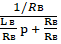
Обозначим.

.

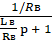
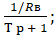
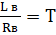
где:

Rв = 0,5 Ом;

Lв = 3 Гн = 3 Ом сек;

Тогда:

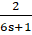
= - апериодическое звено.