Лекция 3. Распространение колебаний в однородной cплошной среде бегущие волны

В природе и технике мы встречаем огромное разнообразие волн: волны и зыбь океанов, волны землетрясений, сейсмические волны, волны звука, волны в натянутой струне или в кРисталле кварца, который используется для излучения или приема ультразвука, электромагнитные волны — свет, радио и даже волны вероятности (!), которые рассматривает квантовая механика при изучении поведения электронов, атомов и т. п.

При всех различиях в происхождении и проявлении волн они обладают целым рядом общих свойств. Эти свойства могут быть выявлены и математически описаны в общем виде, одинаковом для различных физических систем. Установив, что явление определяется волнами, мы можем предсказать многие особенности явления независимо от механизма возбуждения и передачи волн.

Наша задача — выяснить некоторые общие свойства волн на примере волн механических. Как можно возбудить механические волны?

Система, помещенная в какую-либо среду (например, в воздух пли в воду), колеблясь, взаимодействует с частицами, находящимися в прилегающем слое среды. Она создает непрерывный ряд импульсов деформаций, следующих один за другим и распространяющихся в среде. Если скорость распространения каждого отдельного импульса не зависит от их амплитуд и формы (пока импульсы достаточно малы), то они распространяются, следуя в порядке их возбуждения колеблющейся системой, сохраняя свою первоначальную форму.

Положим, система колеблется по гармоническому закону, тогда вынуждающая сила, с которой она действует на прилегающие частицы среды, заставляя их колебаться, также меняется по гармоническому закону. Частицы среды колеблются с частотой вынуждающей силы, т. е. с частотой колебания системы.

Будем считать границу среды настолько удаленной от источника колебаний, что возмущения не успевают за время наблюдения отразиться от нее, и затухание колебаний настолько малым, что им можно пренебречь.

Частицы среды, прилегающие к колеблющейся системе, приходят в колебание одновременно с возникновением колебаний системы. Очевидно, частица, отстоящая от системы на расстоянии x в направлении распространения колебаний, начнет колебаться, когда до нее дойдет начало распространяющегося в среде возмущения. Пусть скорость распространения возмущения в среде с.

Если колебания системы происходят по закону:

,

То точка среды, отстоящая от нее на расстоянии х ,колеблется по тому же закону, но в момент t она имеет смещение, которое имела частица, прилегающая к возмущающей системе, в момент.

.

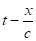
Таким образом, частицы среды смещаются по закону:

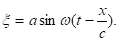
Это уравнение носит название уравнения бегущей волны. Оно определяет величину смещения частицы от положения равновесия как функцию времени t и ее расстояния х от источника возмущения.

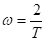
Введем вместо частоты период () :

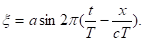
Если зафиксировать определенное значение времени t, то уравнения (1) и (2) дадут нам распределение смещений частиц вдоль направления распространения волн в зависимости от расстояния х. Смещения точек, отстоящих друг от друга на расстоянии х=сТ, в один и тот же момент времени t1 будут, как следует из равенства (3), одинаковы. Следовательно, распространение колебаний в среде — периодический в пространстве процесс. Если в уравнении (1) зафиксируем значение x=x1, т. е. выделим в среде определенную частицу, отстоящую на x1 от источника колебаний, то закон ее колебания:

где.

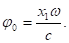
Колебания в каждой точке среды — процесс периодический во времени.

Процесс распространения колебаний в сплошной среде, периодический во времени и в пространстве, называется волновым процессом.

Расстояние между двумя частицами среды, испытывающими в один и тот же момент времени одинаковое смещение, называется длиной волны л. Как мы видели выше, длина волны равна расстоянию, которое проходит волна за один период:

л=сТ.

Равенство (3) можно записать в виде.

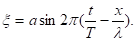
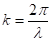
Частицы среды колеблются с одинаковой амплитудой, но точка, отстоящая на x1 от начальной, имеет относительно нее сдвиг фаз. На расстоянии одной длины волны фаза колебания изменяется на 2р. Величину — называют волновым числом. Оно показывает, сколько длин волн укладывается на отрезке длиной 2р. Вводя волновое число, уравнение бегущей волны можно записать в виде.

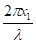
Уравнения (2), (3), (4) и (5) совершенно равноправны. Они описывают один и тот же волновой процесс.

Как и в случае распространения импульса, частицы среды не перемещаются вслед за волной. При прохождении волны они лишь колеблются около положения равновесия. Еще в XV в. Леонардо да Винчи, гений, соединявший в себе наблюдательность художника и интуицию ученого, писал: «Волнения гораздо подвижнее воды, поэтому часто случается так, что волна ускользает от места ее возникновения, а вода остается на том же месте, подобным же образом ведут себя волны, создаваемые ветром на некошеном поле: волны бегут по полю, а стебли злака остаются на месте».

Скорость распространения волны с — это скорость распространения возмущения, вызывающего смещение частиц от положения равновесия. Если на поверхность озера положить в направлении распространения волн веревку с пробковыми поплавками, отстоящими друг от друга на равных расстояниях, то легко заметить, что поплавки и веревка в целом не перемещаются в направлении движения волны. Они лишь поднимаются и опускаются, причем в известной и постоянной последовательности.

Мы видели, что точки, отстоящие друг от друга на расстоянии, равном длине волны л=сТ, колеблются в одинаковой фазе. Можно сказать, что фаза за время одного периода «пробегает» расстояние л или движется со скоростью с. Поэтому скорость распространения волны называют фазовой скоростью. Если в данной среде скорость распространения импульса не зависит от его величины и формы, фазовая скорость совпадает со скоростью распространения отдельного импульса.

Как следует из уравнения (5),.

.

За время одного полного колебания фиксированной частицы среды (4) волна (2) распространяется на расстояние, равное длине волны. Если частица в секунду совершает н колебаний, то волна проходит н длин волн.

Если смещения частиц среды от положения равновесия в волне параллельны направлению ее распространения, волна называется продольной, если перпендикулярны — поперечной