К расчету элементов кровельного ограждения пространственного покрытия при локальных нагрузках

Аннотация: В статье рассматривается методика определения напряженно-деформированного состояния упругого составного слоя, лежащего на абсолютно твердом основании. Подобная ситуация имеет место в покрытии с жестким железобетонном настилом, на котором расположен легкий утеплитель и гидроизоляционный ковер. Моделью покрытия при действии локальной нагрузки может служить упругий составной слой, лежащий на абсолютно твердом основании.

По заданным условиям составляется общее решение задачи теории упругости для каждого слоя. Решается система дифференциальных уравнений. Приводится однородное решение этих уравнений. Полученные решения могут служить для исследования различных проблем напряженного состояния составного слоя.

Решение инженерных задач требует определения комплексных корней трансцендентного характеристического уравнения. В настоящей работе корни определены методом Ньютона. Зная корни характеристического уравнения, можно определить напряжения и перемещения в каждой точке составного слоя.

Ключевые слова: абсолютно твердое основание, составной слой, метагармонические решения, интенсивность реакции опоры, смежные опоры, реакция капители.

В настоящее время изучение статических и динамических проблем теории упругости является актуальным для широкого спектра задач [1,2]. В составе пространственного покрытия здания иногда можно выделить элементы, обладающие столь большой изгибной жесткостью, что их можно рассматривать как абсолютно твердые тела, на которые опираются сложные пластинчатые элементы покрытия. Подобная ситуация имеет место в покрытии с жестким железобетонным настилом, на котором расположен легкий утеплитель и гидроизоляционный ковер. Моделью покрытия при действии локальной нагрузки может служить упругий составной слой, лежащий на абсолютно твердом основании.

Целью настоящей статьи является изложение методики определения напряженно-деформированного состояния указанного слоя.

Пусть верхний упругий слой покоится на нижнем слое, а нижний — на гладком абсолютно твердом основании. Толщина верхнего слоя 2 h₁;

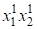
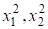
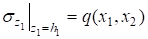
(,) — вектор упругого смещения верхнего слоя; Е₁ — модуль Юнга; ?_1- — коэффициент Пуассона. Толщина нижнего слоя h₂; (,) — вектор упругого смещения нижнего слоя; Е₂ — модуль Юнга; ?_2- — коэффициент Пуассона. Примем срединную плоскость верхнего слоя за плоскость прямоугольной декартовой системы координат, а плоскость основания примем за плоскость. Совместим ось z₁ с осью z₂; оси, направим параллельно соответственно осям .

Предположим, что торцевые поверхности слоев гладкие и верхняя торцевая поверхность первого слоя загружена нормальной нагрузкой:

напряженный деформированный упругий твердый.

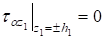
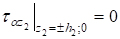
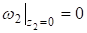
;; ;, (1).

;; .

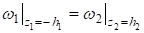
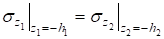
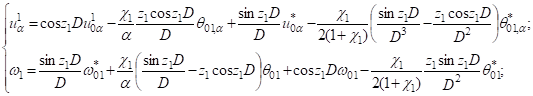
По условиям (1) запишем общее решение задачи теории упругости для каждого слоя [3, 4]. Для верхнего слоя имеем:

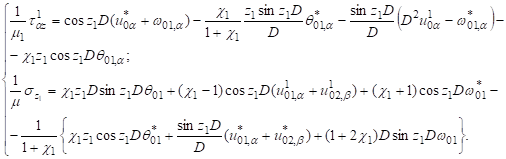
(2).

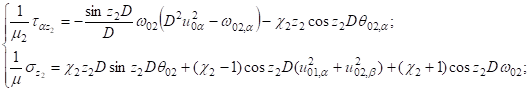
(3).

Для нижнего слоя имеем:

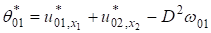
(5).

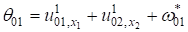
Здесь, ,; .

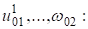
Подставляя выражения напряжений и перемещений (2) — (5) в граничные условия (1), получим систему дифференциальных уравнений для определения девяти неизвестных функций.

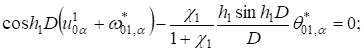
(6).

(7).

(8).

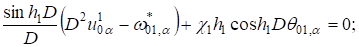
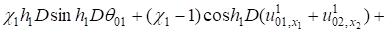
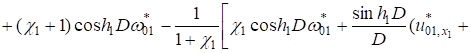
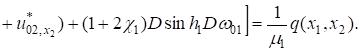
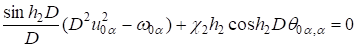
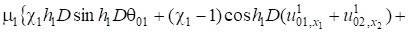
(9).

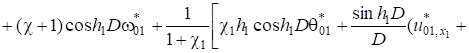
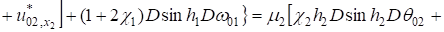
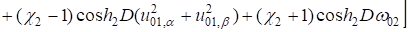
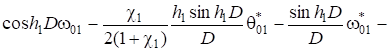
; (10).

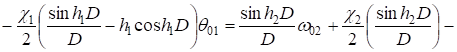
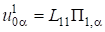
(11).

;

Построим потенциальное решение системы (6) — (11).

Пусть.

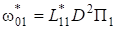
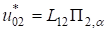
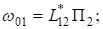
;;; (12).

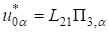
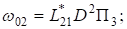
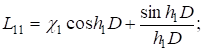
где П₁, П₂, П₃ искомые функции, L_ij — некоторые дифференциальные операторы. Система уравнений (6) — (7) допускает тождественное решение, если L_ij имеют вид.

;

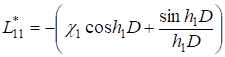
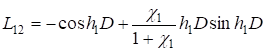
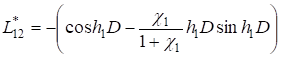
; (13).

;

;

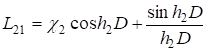
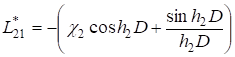
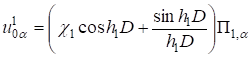
Подставляя (13) в (12), получим.

; ;

; ;

;

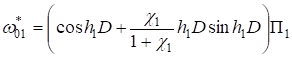
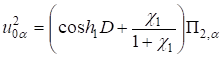
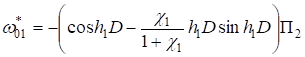
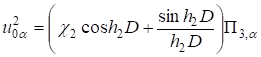
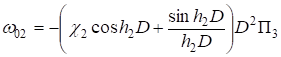
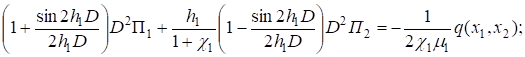
(14).

Из (8), (10), (11), (14) получаем систему уравнений для функций.

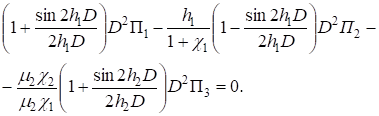
(15).

(16).

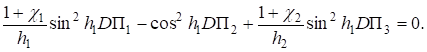
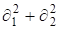
(17).

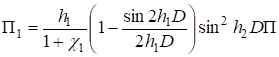
Задача свелась к решению системы дифференциальных уравнений (15) — (17). Рассмотрим однородное решение этих уравнений[5]. Основываясь на том, что операторы дифференцирования ?₁, ?₂, D²? подчиняются тем же формальным правилам сложения и умножения, что и числа, выразим функции П_i через новую функцию напряжений П по формулам.

; ;

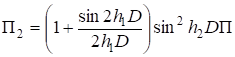
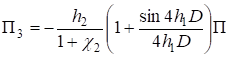
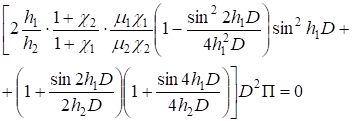
. (18).

Подставляя выражения (18) в (16), получаем уравнение для определения П.

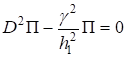
(19).

Легко получить счетное множество решений этого уравнения[6,7]. Для этого предположим, что функция П удовлетворяет уравнению Гельмгольца.

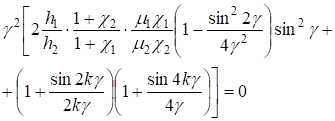
(20).

где ?² — некоторый параметр. Характеристическое уравнение получим из (19) и (20).

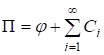
(21).

где k = h₂/h₁. Из (21) следует, что решение уравнения (19) можно представить в виде суммы — гармонического решения ? и счетного множества метагармонических решений С_i, отвечающих соответствующим корням ?_i уравнения (21).

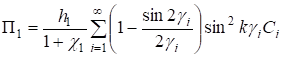
(22).

Рассмотрим метагармонические решения. В силу линейности задачи, функции П_i, из (18) представим в виде.

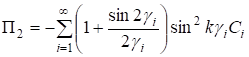
; (23).

;

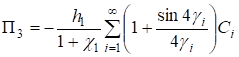
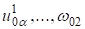
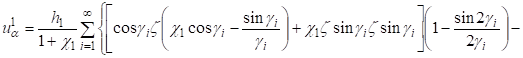
Пользуясь операторами (14), определим функции и подставим их в выражения компонентов вектора упругого смещения и тензора напряжений (2) — (5). Для верхнего слоя получаем метагармоническое решение.

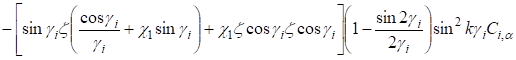
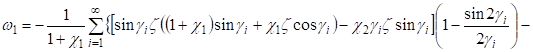
(24).

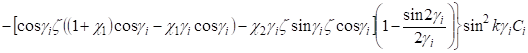
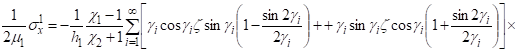
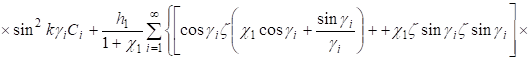
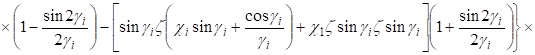
(25).

.

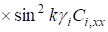
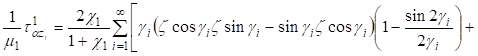
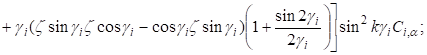
(26).

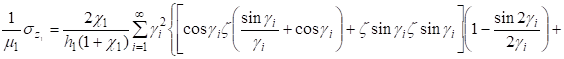
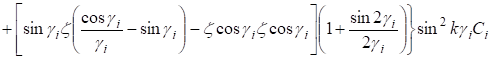
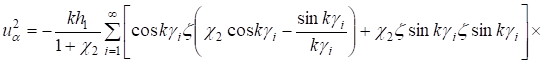
(27).

Для нижнего слоя имеем:

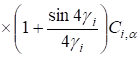
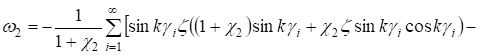
; (28).

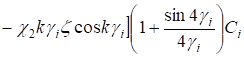
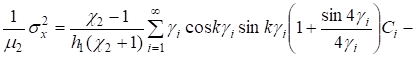
; (29).

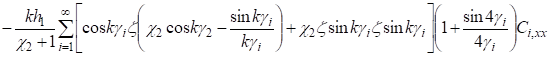
(30).

;

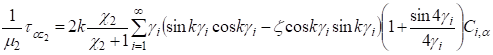
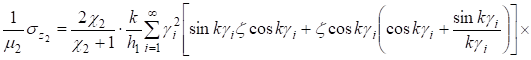
(31).

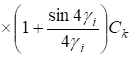
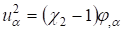
(32).

Что касается Рассмотрим метагармонические решения, то любая гармоническая функция? может служить решением разрешающего дифференциального уравнения (19). Легко указать, что гармоническое решение определяет напряженно-деформированное состояние нижнего слоя по формулам.

; ;

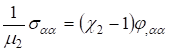
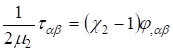
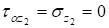
;; (33).

.

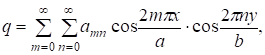
Полученные решения могут служить для исследования различных проблем напряженного состояния составного слоя[8].

Решение конкретных инженерных задач требует определения комплексных корней трансцендентного характеристического уравнения (21). В настоящее работе корни определялись методом Ньютона. В качестве начальных приближений взяты асимптотические представления корней в зависимости от номера корня. Для различных значений k = h₂/h₁ вычислялись по 30 комплексных корней. В таблице 1 приведены значения корней для К? 5, 10, 20. Численный анализ показывает, что с увеличением К, т. е. уменьшением толщины второго слоя или утолщением первого слоя, вещественная часть корней уменьшается[9]. Компоненты напряженно-деформированного состояния начинают медленнее затухать при удалении от границы. Зная корни характеристического уравнения, можно определить напряжения и перемещения в каждой точке составного слоя.

Таблица 1.

Корни характеристического уравнения.

В качестве примера построения неоднородного решения системы (15)-(17) рассмотрим задачу бесконечно простирающегося безбалочного покрытия, состоящего из верхнего слоя толщиной h₂ и нижнего слоя толщиной 2h₁. Внешняя поверхность покрытия нагружена равномерно распределенной нагрузкой и не имеет прогиба. Нижний слой покрытия подпирается прямоугольными капителями колонн, отстоящих друг от друга на одинаковых расстояниях. Будем считать, что реакция капители равномерно распределена по поверхности опоры … Интенсивность реакции опоры легко определить из условий симметрии задачи. Решение задачи теории упругости такого покрытия можно получить в двойных рядах Фурье.

Условия симметрии допускают представить реакцию колонн в виде ряда косинусов.

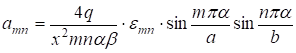
(34).

где а и b — расстояния центров смежных опор. Интенсивность реакции опоры равна q/??? внутри прямоугольника и равна нулю по всей остальной площади нижней торцевой поверхности слоя. Поэтому для коэффициентов а_mn получаем выражение.

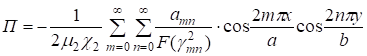
(35).

где.

для, ;

для, ;

;

для, .

В частном случае или коэффициенты получаются непосредственно как предельное значение выражения (35).

Из (19) — (21), (35), (36) получаем для функции напряжений П выражение.

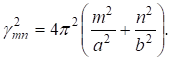
(36) где.

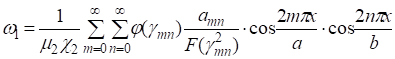
(37).

Выражение (36) полностью решает задачу напряженно-деформированного состояния данного покрытия[10]. Здесь приведем лишь выражение прогиба нижней поверхности покрытия.

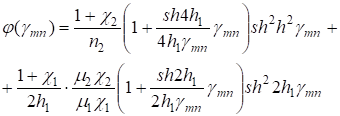
(38).

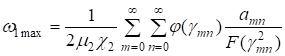
(39).

В центре прямоугольника прогиб принимает максимальное значение.

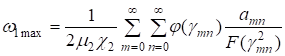
(40).

В таблице 2 приводится ряд значений максимальных прогибов при различных значениях отношений h₁/ h₂, ?₁/?₂, ?₁/?₂, а? b.

Таблица 2

Максимальный прогиб нижней поверхности многослойного покрытия на прямоугольных капителях.

Кадомцев М.И., Ляпин А. А., Шатилов Ю. Ю. Вибродиагностика строительных конструкций // Инженерный вестник Дона. 2012. № 3URL:ivdon.ru/magazine/archive/n3y2012/941.

Зотов А.В., Ляпин А. А. К анализу температурных напряжений в бетонных покрытиях // Инженерный вестник Дона. 2013. № 4 URL: ivdon.ru/ru/magazine/archive/n4y2013/2083.

Лурье А.И. К теории толстых плит // ПММ. 1942. Т. 6. Вып. 2−3, С. 151−168.

Лурье А. И. Пространственные задачи теории упругости. М., 1955. 491 с.

Тр. Американского общества инж. -механ, 1969. Т. 36. № 4, С. 151−155.

Шарый С. П. Курс вычислительных методов. Новосибирск: Институт вычислительных технологий СО РАН, 2016. 526 с.

Воеводин В. В. Линейная алгебра. М.: Наука, 1980, 400 с.

Chen W.L., Striz A.G., Bert C.W. High-accuracy Plane Stress and Plate Elements in the Quadrature Element Method. International Journal of Solids and Structures. 2000, vol. 37, no. 4, pp. 627—647. URL: dx.doi.org/10.1016/S0020−7683 (99)00028−1.

Головина Л. И. Линейная алгебра и некоторые ее приложения. М., Наука, 1979. 392 с.

Wen P.H. The Fundamental Solution of Mindlin Plates Resting on an Elastic Foundation in the Laplace Domain and its Application. International Journal of Solids and Structures. 2008, vol. 45, no. 3, pp. 1032—1050. URL: dx.doi.org/10.1016/j.ijsolstr.2007.09.020.

References

Kadomcev M.I., Ljapin A.A., Shatilov Ju.Ju. Inћenernyj vestnik Dona (Rus), 2012. № 3 URL: vdon.ru/magazine/archive/n3y2012/941/.

Zotov A.V., Ljapin A.A. Inћenernyj vestnik Dona (Rus), 2013. № 4 URL: ivdon.ru/ru/magazine/archive/n4y2013/2083/.

Lur’e A.I. PMM. 1942. T. 6. Vyp. 2−3, pp. 151−168.

Lur’e A.I. Prostranstvennye zadachi teorii uprugosti [Spatial problems of the theory of elasticity]. M., 1955, 491 p.

Tr. Amerikanskogo obshhestva inzh.-mehan., 1969. T. 36. № 4, pp. 151−155.

Sharyj S.P. Kurs vychislitel’nyh metodov. [The course Computational Methods Novosibirsk: Institut vychislitel’nyh tehnologij]. SO RAN, 2016, 526 p.

Voevodin V.V. Linejnaja algebra [Linear algebra] M.: Nauka, 1980, 400 p.

Chen W.L., Striz A.G., Bert C.W. High-accuracy Plane Stress and Plate Elements in the Quadrature Element Method. International Journal of Solids and Structures. 2000, vol. 37, no.4, pp. 627—647. URL: dx.doi.org/10.1016/S0020−7683 (99)00028−1.

Golovina L.I. Linejnaja algebra i nekotorye ee prilozhenija [Linear algebra and some of its applications]. M., Nauka, 1979. 392 p.

Wen P.H. The Fundamental Solution of Mindlin Plates Resting on an Elastic Foundation in the Laplace Domain and its Application. International Journal of Solids and Structures. 2008, vol. 45, no. 3, pp. 1032—1050. URL: dx.doi.org/10.1016/j.ijsolstr.2007.09.020.