Оптимизация на основе вероятностного подхода нечетких моделей управления производственными объектами управления

В статье рассматривается задача оптимизации нечеткой модели управления. Для производственных процессов, функционирующих в условиях априорной неопределенности, используются нечеткие методы управления, на основе которых разрабатываются системы управления. В качестве примера производственного процесса, функционирующего в условиях априорной неопределенности, рассматривается процесс управления температурой в хлебопекарной камере. После разработки нечеткой модели управления температурой в хлебопекарной камере выполняется оценка ее результатов, при отклонении от требуемых значений точности осуществляется оптимизация. В качестве методов оптимизации применяются вероятностные методы. В качестве параметра оптимизации используются функции принадлежности нечеткой модели. Задаются параметры точности и их пороговые значения для оценки нечеткой модели. В работе приведены результаты моделирования и параметры нечеткой модели до оптимизации и после. оптимизация нечеткий производственный управление.

Ключевые слова: нечеткая модель, алгоритм оптимизации, теория вероятности, оценка точности, функции принадлежности.

Нечеткие методы управления являются альтернативой традиционных методов для задач управления производственными объектами (ПОУ), функционирующими в условиях априорной неопределенности, поскольку, с одной стороны, нечеткая логика позволяет описывать качественную информацию, нечеткость, недостоверность, неполноту данных о ПОУ и среде его функционирования. А с другой стороны, нечеткие методы обеспечивают эффективный процесс управления без нахождения математической модели рассматриваемым ПОУ [1, 2].

Для повышения точности нечеткой модели управления ПОУ и устранения субъективности при экспертном задании параметров нечеткой модели, целесообразно выполнить оценку ее результатов и при необходимости оптимизацию. В качестве метода оптимизации предлагается применять методы, основанные на теории вероятности. Этот выбор можно объяснить проработанностью математического аппарата теории вероятности, близостью нечеткости и вероятности, и, следовательно, возможностью оперирования вероятностными и нечеткими вычислениями в процессе оптимизации [3].

Разработка нечеткой модели управления ПОУ на примере управления температурой в хлебопекарной камере. Зададим параметры нечеткой модели управления температурой в хлебопекарной камере [4]:

Терм-множества входных переменных: T — текущее значение температуры в хлебопекарной камере: T: <T₁; T₂; T₃; T₄; T₅>; Z — нагрузка печи: Z: <Z₁; Z₂; Z₃>; P— расход пара: P: <P₁; P₂; P₃; P₄; P₅>.

Терм-множества для выходных переменных: G — расход топлива: G:<G₁; G₂; G₃; G₄; G₅>; V-расход воздуха: V<V₁; V₂; V₃; V₄; V₅>.

В качестве алгоритма нечеткого логического вывода выбирается алгоритм Мамдани, это связано с видом используемых правил. Экспертным путем формируется база продукционных правил, число правил в которой определяется, как произведение термов всех входных переменных: z =T*Z*P, для рассматриваемой задачи число правил составляет: z = 75.

Для оценки точности нечеткой модели управления температурой в хлебопекарной камере выбирается среднеквадратическое отклонение по расходу топлива (СКО) [5, 6] (1):

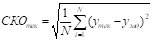
СКО_тек? СКО_зад?5%, (1).

N — число моделирований; СКО_тек — текущее значение ошибки; СКО_зад — заданное значение ошибки; y_тек — полученное значение переменной; y_зад — заданное значение переменной.

Эксперты определяют заданные значения только для одной выходной переменной «расход топлива», значения переменной «расход воздуха» изменяются пропорционально.

В качестве второго параметра для оценки точности нечеткой модели управления и слежения за состоянием рассматриваемого ПОУ выбирается соотношение между сжигаемым топливом и подаваемым воздухом. Для природного газа данное соотношение должно находиться в пропорции [7] (2):

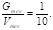
(2).

Далее выполняется проведение экспериментального исследования разработанной нечеткой модели управления температурой в хлебопекарной камере для 200 примеров. На данном этапе исследование выполняется без учета блока оптимизации. Каждый раз входные значения формируются случайным образом. Результаты работы нечеткой модели показаны на рис. 2:

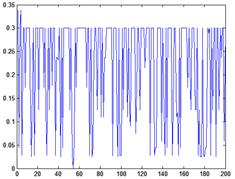
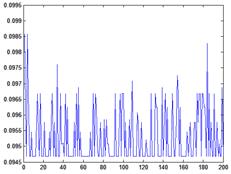
а б, а — график СКО; б — соотношение топливо-воздух Рис. 2 Результаты работы нечеткой модели управления температурой в хлебопекарной камере

Значения, полученные в результате эксперимента можно объединить в таблицу 1:

Таблица 1

Результаты работы нечеткой модели управления.

Анализируя полученные значения параметров оценки нечеткой модели управления ПОУ, можно сделать вывод, что в среднем значение СКО за один цикл моделирований удовлетворяет поставленному условию (1) и не превышает 2,12%. Однако максимальное значение СКО в отдельных примерах превышает пороговое значение 5% (1) и составляет 0,36. Для второго параметра оценки — соотношения между сжигаемым топливом и подаваемым воздухом среднее значение составляет 0,0986. Полученное значение не соответствует заданному уровню 0,1 (2).

В ходе использования нечетких методов управления удалось построить модель управления ПОУ, функционирующим в условиях априорной неопределенности, для которого нет точной математической модели [8]. Но полученные результаты не в полной мере удовлетворяют заданным параметрам точности. Для повышения точности разработанной нечеткой модели предлагается выполнить ее оптимизацию.

Задание алгоритма оптимизации на основе вероятностных методов для нечеткой модели управления ПОУ. Разрабатываемый алгоритм оптимизации рассматривается на примере нечеткой модели управления температурой в хлебопекарной камере.

В качестве параметра оптимизации выбираются функции принадлежности (ФП). ФП покрывают все множество значений переменных. Для разработки нечеткой модели и настройки выбираются треугольные ФП, это связано с удобством их использования, распространенностью и простотой [9]. Треугольную ФП можно задать с помощью трех чисел, соответствующих оси абсцисс, и определяющих положение ее границ и вершины: A, B, C.

Настройка параметров нечеткой модели управления ПОУ на основе вероятностного подхода, предполагает использование тех же способов оценки, что и для случайных величин, поскольку нечеткие события, это те же события, но происходящие в неопределенных условиях [3] По результатам моделирования строятся гистограммы частот эмпирических функций распределения каждой ФП.

По полученным статистическим данным выполняется проверка гипотезы о соответствии построенных эмпирических функций распределения теоретическим [10], на основании значений критерия Пирсона и графиков эмпирических функций распределения ФП можно утверждать, что они имеют вид нормального распределения [11].

Поэтапно работа алгоритма оптимизации на основе вероятностного подхода состоит из следующих этапов:

Этап 1. Проведение серии моделирований. Проводится серия моделирований, фиксируются значения всех входных и выходных переменных и частота их попадания в заданные интервалы каждой ФП.

Этап 2. Вычисление математического ожидания для всех ФП [10] (3):

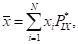
(3).

где x_i — текущее значение ФП;- среднее значение ФП.

Этап 3. Определение СКО для всех ФП. На основе полученных данных и математического ожидания вычисляется СКО для каждой ФП [10] (4):

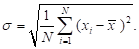
(4).

Этап 4. Построение интервала по правилу трех сигма. Поскольку принимается, что графики эмпирических функций распределения, полученных на основе ФП, имеют нормальное распределение, то применяется правило трех сигма для настройки границ ФП. С заданной точностью можно сказать, что практически все значение нечеткой переменной попадет в диапазон (5):

. (5).

Этап 5. Настройка границ ФП. После определения новых границ ФП в соответствии с формулой (5), выполняется корректировка диапазона ФП. Изменяются только границы ФП, вершины остаются прежними.

Далее выполняется вторая часть настройки ФП — корректировка положения вершины ФП. Необходимо выполнить оценку положения вершины ФП и при необходимости скорректировать ее.

Выполняется повторение этапов 1 и 2.

Этап 6. Определение оценки СКО. После нахождения математического ожидания, вычисляется оценка СКО каждой ФП (6):

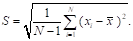
(6).

Этап 7. Построение доверительного интервала для вершин ФП. Для полученных значений математического ожидания и оценки СКО строится доверительный интервал, определяющий положение вершины ФП [10] (7):

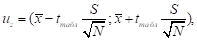
(7).

где u_z — доверительный интервал; t_табл — критерий Стьюдента.

Этап 8.°Разбиение доверительного интервала ФП. Определенный ранее доверительный интервал вершины для ФП делится на некоторое число участков l_z, в данном случае принимается, что z = 5, а все участки l_z равны.

Этап 9. Определение положения вершины ФП. После проведения экспериментальных исследований определяется участок l_z с максимальным числом попаданий в него значений переменных. При совпадении вершины ФП и диапазона с максимальным числом попаданий, изменений не происходит.

Этап 18.Вывод новых ФП. После выполнения настройки границ и корректировки положения вершины ФП получаются оптимальные значения ФП, и затем выполняется вывод новых ФП.

Этап 19. Оценка полученных результатов. Результаты работы нечеткой модели управления ПОУ без учета блока оптимизации сравниваются с показателями, полученными после применения алгоритма оптимизации. Определяется эффективность разработанного алгоритма оптимизации нечеткой модели управления ПОУ на основе вероятностных методов.

Проведение экспериментальных исследований разработанного алгоритма оптимизации на основе теории вероятности для нечеткой модели управления ПОУ. Используя исходные значения экспериментальных исследований (Таблица 1), выполняется процесс оптимизации. Алгоритм оптимизации выполняется до тех пор, пока значения показателей точности не достигнут заданного уровня (1) и (2) рис. 5.

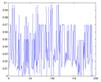
а б в г д.

е ж з и к а, б, в, г, д — графики СКО по расходу топлива; е, ж, з, и, к — графики соотношения топливо-воздух Рис. 5 Результаты работы алгоритма оптимизации для нечеткой модели управления температурой в хлебопекарной камере

После выполнения алгоритма оптимизации значения параметров точности заносятся в таблицу 2:

Таблица 2.

Результаты работы алгоритма оптимизации.

По результатам таблицы 2 можно проследить динамику в работе алгоритма оптимизации нечеткой модели управления ПОУ. После выполнения 5 итераций СКО в среднем снизилось с 0,021 до 0,0005. Максимальное значение СКО снизилось в 10,2 раза с 0,36 до 0,3 523. Полученные значения СКО удовлетворяют условию (1) и не превышают 5%.

Второй параметр точности топливо-воздух в среднем достиг требуемого значения (2) и составляет практически 0,1. Скорректированные значения ФП представлены на рис.6:

а б в г.

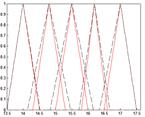
д а, б, в, г, д — графики ФП T; Z; P; G; V

Рис. 6 Графики ФП до и после оптимизации

Заключение

В данной работе исследовалась задача оптимизации нечеткой модели управления ПОУ. Была разработана нечеткая модель управления ПОУ и проведен анализ ее работы без учета блока оптимизации. Затем выполнена оптимизация нечеткой модели управления ПОУ: настройка границ ФП, оценка и корректировка положения вершин ФП.

Разработанный алгоритм оптимизации на основе вероятностного подхода является универсальным способом настройки параметров нечетких моделей управления ПОУ. Использование связи между ФП и функцией распределения позволяет применять методы теории вероятности, благодаря чему снижается ошибка, полученная по итогам субъективного задания параметров нечеткой модели ПОУ, что приводит к повышению точности результатов и достижению оптимальных показателей управления.

• 1. Заде Л. А. Понятие лингвистической переменной и его применение к принятию приближенных решений. М.: Мир, 1976. 165 с.
• 2. К. Асаи. Прикладные нечеткие системы // К. Асаи, Д. Ватада, С. Иваи; под ред. Т. Тэрано, К. Асаи, М. Сугэно. М.: Мир, 1993. 184 p.
• 3. Zadeh L.A., 1968, Probability measures of Fuzzy events Journal of Mathematical Analysis and Applications. Vol. 23: 421−427.
• 4. Синявская Е. Д. Анализ точности работы нечеткой модели и оптимизация ее параметров на примере управления температурой в хлебопекарной камере. Материалы ІІ Всероссийской научно-практической конференции «Молодежь, наука, инновации», Грозный. 2013. с. 95−100.
• 5. Alp Yanar T., Akyьrek Z., 2011, Fuzzy model tuning using simulated annealing, Expert Systems with Applications. № 38: 8159−8169.
• 6. Штовба С. Д. Обеспечение точности и прозрачности нечеткой модели Мамдани при обучении по экспериментальным данным // Проблемы управления и информатики. 2007. № 4. с. 1 — 13.
• 7. Стаскевич Н. Л., Северинец Г. Н. Вигдорчик Д.Я. Справочник по газоснабжению и использованию газа. Л.: Недра, 1990. 762 с.
• 8. Курсовое и дипломное проектирование по автоматизации производственных процессов / под ред. И. К. Петрова. М: Высшая школа, 1986. 352 с.
• 9. Штовба С. Д. Проектирование систем управления Fuzzy Logic Toolbox. URL: http://matlab.exponenta.ru/.
• 10. Гмурман В. Е. Теория вероятностей и математическая статистика. М.: Высшая школа, 2003. 479 с.
• 11. Baudrita C., Duboisb D., Perrota N., 2008. Representing parametric probabilistic models tainted with imprecision. Fuzzy Sets and Systems. 159: 1913 — 1928.