Анализ стадии эксплуатации и разрушения нормального сечения изгибаемого железобетонного элемента

В экспериментах на железобетонных балках было неоднократно зафиксировано, что уменьшение высоты сжатой зоны с увеличением нагрузки в некоторых случаях сменяется увеличением, а затем снова (хотя и не всегда) уменьшением. Выяснение условий таких «флуктуаций» важно для полноты картины напряжённо-деформированного состояния эксплуатационной стадии, поскольку при некоторых уровнях развития поперечные трещины меняют направление развития и становятся продольными. В случае особых воздействий, в частности сейсмических, когда при проектировании допускаются локальные разрушения (без обрушения конструкций) необходимо более детальное изучение стадии разрушения, которая представляет собой не мгновенный акт, а состоит из разных фаз в зависимости от соотношения деформаций в сжатом бетоне и растянутой арматуре.

1. Постановка задачи

Рассмотрим плоскую задачу для изгибаемого железобетонного элемента, в котором нижние волокна растянуты, верхние — сжаты. Диаграмму деформирования бетона примем в виде двухзвенной кусочно-линейной функции с характерными точками (еbt1, Rbt), (0,0), (еb1, Rb), (еb2, Rb) (в соответствии с СП 63.13 330.2012 и [1]). Диаграмму деформирования арматуры — в виде двухзвенной в сжатой зоне и четырёхзвенной в растянутой зоне кусочно-линейной функции с характерными точками (еsc0, Rsc), (еsc1, Rsc), (0,0), (еs1, Rs), (еs2, Rs), (еs3, Rsu), (еs4, Rsu) (в соответствии с СП 63.13 330.2012 и [2]).

Использованные обозначения:

еbt1=Rbt/Eb, еb1=Rb/Eb;

Rbt, Rb, Eb — сопротивление бетона растяжению, сжатию и начальный модуль упругости бетона, еb2 — предельная сжимаемость бетона; еsc0, Rsc — деформация и напряжение в сжатой арматуре, соответствующие предельной сжимаемости бетона; еsc1=Rsc/Es, Es — модуль упругости арматуры; еs1=Rs/Es — деформация, соответствующая началу площадки текучести, еs2 — деформация, соответствующая концу площадки текучести, еs3 — деформация соответствующая концу ветви упрочнения, еs4 — деформация соответствующая разрыву арматуры; Rs, Rsu — расчётное сопротивление арматуры по пределу текучести и расчётное сопротивление арматуры по временному сопротивлению.

Неупругие деформации в растянутой зоне бетона перед образованием трещины и в её вершине в процессе развития моделируются зоной предразрушения, трактовка которой с позиций механики разрушения взята из книги [3]. Распределение деформаций в нормальном сечении при их осреднении принято по теории В. И. Мурашёва [4] подчиняющимся гипотезе плоских сечений [5].

2. Результаты

Следуя методике, изложенной в [3] и использованной в работах [6−7], запишем геометрические соотношения, связывающие между собой деформации различных точек нормального сечения изгибаемого элемента. После образования трещин деформированная ось элемента получает волнообразный вид с минимальной высотой сжатой зоны в сечении c трещиной х=оh=xm ц, (1).

где х — высота сжатой зоны в сечении с трещиной; h — высота нормального сечения элемента; о — относительная высота сжатой зоны (оh=х/h); xm — среднее значение высоты сжатой зоны в пределах расстояния lcrc между соседними поперечными трещинами; ц — коэффициент осреднения высоты сжатой зоны (ц<1).

Эти и другие обозначения видны из расчётной схемы элемента на рисунке 1.

Рисунок 1 Расчётная схема железобетонного элемента с трещинами при нелинейном деформировании бетона сжатой зоны

Деформации волокон сжатой и растянутой зон по длине элемента между соседними трещинами, как и высота сжатой зоны, также неравномерны с наибольшими значениями (еb, еs1, еs) в сечении с трещиной и наименьшими — между трещинами. Коэффициенты осреднения деформаций на участке между соседними трещинами связывают между собой деформации в сечении с трещиной шb=еbm/еb=еs1m/еs1, шs=еsm/еs, (2).

где обозначения с индексом m относятся к средним деформациям, а без индекса m — к деформациям в сечении с трещиной.

Согласно гипотезе Я. Бернулли [5] для сечения с трещиной имеем:

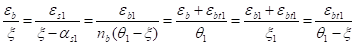
(3).

где бs1=a1/h, бs=a/h — относительная толщина защитного слоя сжатой и растянутой арматуры; nb=еb1/еbt1=(Rb/Eb)/(Rbt/Eb)=Rb/Rbt — отношение прочности бетона при сжатии к прочности бетона при растяжении; остальные обозначения ясны из рисунка 1.

Геометрические соотношения (3) справедливы лишь в сжатой зоне. Деформация растянутой арматуры в сечении с трещиной в общем случае «не укладывается» на линию, продолжающую линию деформаций сжатой зоны. Но осреднённые деформации и сжатой и растянутой зон, как показано в различных исследованиях (например, [8−9]), вполне подчиняются гипотезе плоских сечений.

Геометрические соотношения осреднённых деформаций:

.

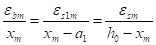
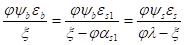
. (4).

Из равенств (3) вытекают следующие выражения:

еb=еbt1о/(и1-о), о=еbи1/(еb+еbt1),.

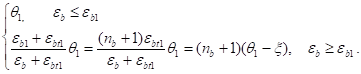
о1= (5).

Равенства (4) дают после несложных преобразований:

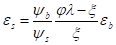
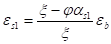
, (6).

где л=h0/h, h0=h-a, л=h0/h=(h-a)/h=1-бs, бs=a/h, бs1=a1/h.

В дальнейшем полезен также иной вид еs1, с учётом еb:

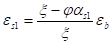
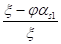
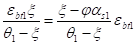
=*. (7).

Как и в [3, 6−7, 10−11], распределение напряжений на продолжении трещины представим в виде двух эпюр: трапециевидной в сжатой зоне с нулевым значением в вершине трещины (она может быть и треугольной, если еb? еb1) и треугольной в растянутой зоне со значением Rbt в вершине трещины (рисунок 1).

Определим дополнительные геометрические характеристики, необходимые для вычисления усилий в бетоне при составлении уравнений равновесия.

Поскольку модифицированная эпюра напряжений в сжатой зоне в общем случае имеет вид трапеции, то усилие здесь можно определить по формуле.

Nbc=Rbbhи1щ, (8).

где b — ширина сечения; и1 — относительная высота части сечения над трещиной (и1=1-и, и=hcrc/h); щ — коэффициент полноты эпюры напряжений, равный в условиях плоской задачи отношению площади расчётной эпюры (например, трапеции, как на рисунке 1) к площади объемлющего прямоугольника Rbhи1:

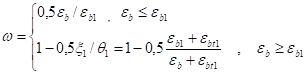
(9).

или.

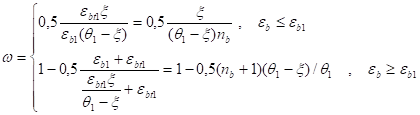
(10).

Формула (9) используется, когда в качестве основной неизвестной принята переменная еb, формула (10), когда основная переменная о.

Центр тяжести модифицированной эпюры напряжений в сжатой зоне, вычисляемый по общему правилу как отношение статического момента площади относительно некоторой оси (в данном случае относительно оси, совпадающей с крайним волокном сжатой грани) к величине этой площади:

y===,.

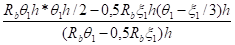
Имея в виду (9) (щ=1−0,5о1/и1), откуда следует о1/и1=2(1-щ), нетрудно получить следующие выражения:

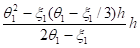
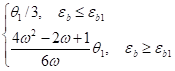
ж1=y/h= (11).

Составим уравнения равновесия задачи: сумму проекций всех сил на продольную ось элемента и сумму моментов всех сил относительно моментной точки, расположенной в центре тяжести растянутой арматуры.

-pbc-ps1+pbt+ ps+pcrc-p=0, (12)

pbc (л-ж1)+ps1(л-бs1)-pbt (л-и1+о1/3)-pcrc (л-и1−2ж/3)+p (л-0,5)-m=0, (13).

где pbc — относительная величина равнодействующего усилия в трансформированной эпюре сжатой зоны бетона:

pbc=Nbc/(Rbtbh)=Rbbhи1щ/(Rbtbh)=nbи1щ=0,5nbи1* (14).

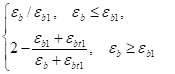
или.

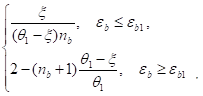
pbc=0,5nbи1* (15).

формула (14) применяется, когда в качестве неизвестного выступает еb, формула (15), — когда искомая величина о;

pbt — относительная величина равнодействующего усилия в трансформированной эпюре растянутой зоны бетона над трещиной:

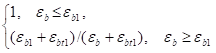
pbt=Nbt/(Rbtbh)=0,5Rbtbhо1/(Rbtbh)=0,5и1* (16).

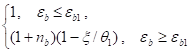
pbt=0,5и1*; (17).

ps1 — относительная величина равнодействующего усилия в сжатой арматуре:

ps1=Ns1/(Rbtbh)=уs1м1bh/(Rbtbh)=еs1Esм1/Rbt=еs1nEEbм1/Rbt=(м1nE /еbt1)еs1.

введя обозначение r1=м1nE и воспользовавшись равенством (7), получим.

ps1=,.

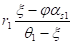
а введя сюда вместо о его форму из (5) будем иметь выражение.

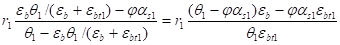
ps1=,.

которое, как и предыдущее, справедливо на линейном участке диаграммы деформирования сжатой арматуры, в случае перехода её на площадку текучести оно получает иной вид.

ps1=Rscм1bh/(Rbtbh)=(Rsc/Rbt)м1=nуscм1, (18).

то есть.

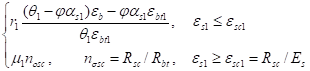
ps1=, (19).

когда в числе основных искомых величин еb, или

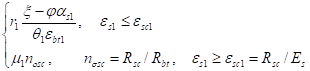
ps1=, (20).

когда в числе основных искомых величин о;

ps — относительная величина равнодействующего усилия в растянутой арматуре:

ps=Ns/(Rbtbh)=уsмbh/(Rbtbh)=еsEsм/Rbt=еsnEEbм/Rbt=(мnE/еbt1)еs ,.

подставим сюда еs из (6).

ps=(мnE/еbt1)еs=(мnE/еbt1) ,.

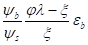
а затем еb из (5).

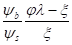
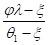
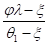
ps=(мnE/еbt1)*еbt1о/(и1-о)=(мnEшb/шs)=r, (21).

r=мnEшb/шs ,;

полученное выражение справедливо в линейной области деформирования растянутой арматуры; на площадке текучести (еs1?еs?еs2), где напряжения уs=Rs остаются постоянными, выражение ps приобретает вид.

ps=Rsмbh/(Rbtbh)=nsRм, nsR=Rs/Rbt, (22).

на ветви упрочнения (еs2?еs?еs3).

уs=Rs+(еs-еs2)Es1,.

ps=уsмbh/(Rbtbh)=муs/Rbt=м[Rs+(еs-еs2)Es1]/Rbt=.

=(мEs/Rbt)[Rs/Es+еsEs1/Es-еs2Es1/Es]=.

=мnEnsEеs/еbt1+мnsR-мnEnsEеs2/еbt1, nsE=Es1/Es ,.

далее подставив сюда еs из (6), а затем еb из (5), придём к выражению.

ps=+мnsR-мnEnsEеs2/еbt1=.

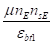
=*+мnsR-мnEnsEеs2/еbt1 =.

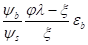
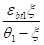
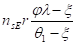
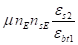
=+мnsR-; (23).

заметим, что формулы (21), (23) применимы, если в качестве искомой величины выступает о; выразив с помощью (5) о через еb, нетрудно получить формулы, применимые в случае, когда искомой величиной является еb:

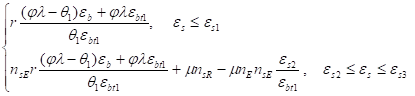
ps=; (24).

на верхней площадке текучести (еs3?еs?еs4) где напряжения уs=Rsu остаются постоянными, для ps выражение будет аналогично (22).

ps=Rsuмbh/(Rbtbh)=nsuм, nsu=Rsu/Rbt; (25).

pcrc — относительная величина равнодействующего усилия в концевой части трещины (в зоне предразрушения), определяемая, как описано в [3]:

pcrc=Ncrc/(Rbtbh)=2ryRbtb/(Rbtbh)=2ry/h=2ж, (26).

ж=ry/h, ry=б0ds, б0= k02/(2р), k0 — эмпирический коэффициент; ds — среднестатистический размер крупного заполнителя бетона;

относительная величина внешнего продольного усилия.

p=N/(Rbtbh). (27).

Поскольку растянутая арматура в принятой расчётной схеме может находиться в четырёх различных состояниях, сжатая арматура — в двух состояниях и сжатый бетон тоже в двух состояниях, общее число вариантов перебора состояний равно 16. Но среди этих состояний есть 4 физически невозможных (когда сжатая арматура находится в пластическом состоянии, сжатый бетон не может быть в упругом состоянии). Поэтому число возможных вариантов решения задачи 12. В каждом из них прочностные, деформационные характеристики материалов, размеры сечений b, h, ry, м, м1, внешние усилия M, N являются заданными величинами. Все усилия в уравнениях равновесия (12) и (13) могут быть выражены, как показано выше (формулы (14) — (24)), через переменные еb и и1, либо о и и1.

Таким образом, получается система двух нелинейных относительно двух неизвестных еb и и1, либо о и и1. Она разрешима тем или способом, и каждой паре значений (M, N) ставится в соответствие пара значений (еb, и1), позволяющая через полученные выше формулы вычислить все параметры напряжённо-деформированного состояния рассматриваемого сечения. Ещё проще достигается результат, если последовательно задаваясь одной из искомых величин, например, и1 (от 1 до 0,1 или 0,05), находить другую (еb или о) из первого уравнения равновесия (12), которое в ряде вариантов оказывается линейным относительно искомого параметра и в любом случае не выше квадратного, а затем по второму уравнению равновесия (13), имеющему более высокий порядок, вычислять значение момента М, соответствующего параметрам (и1,еb) или (и1, о).

Приведём некоторые количественные результаты. На рисунках 2 и 3 приведены зависимости m1=M/(Rbtbh2), относительной высоты зоны над трещиной и1 и относительной высоты сжатой зоны о от деформации крайнего сжатого волокна бетона еb при малых (рисунок 2) и относительно больших (рисунок 3) коэффициентах армирования м.

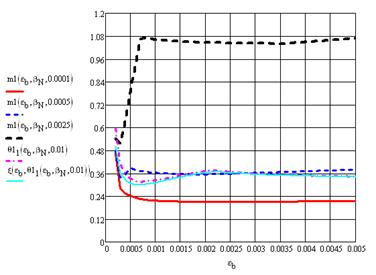
Рисунок 2 Зависимости m1=M/(Rbtbh2), относительной высоты зоны над трещиной и1=(h-hcrc)/h=1-и и относительной высоты сжатой зоны о от деформации крайнего сжатого волокна бетона еb при малых коэффициентах армирования м (третье место в списке аргументов, относительное продольное усилие отсутствует (вn=pn=0)).

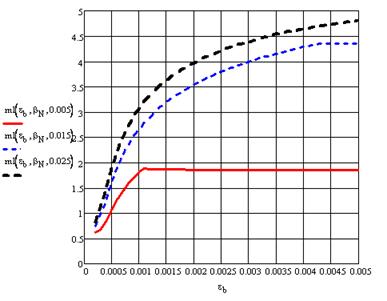
Рисунок 3 Зависимость m1=M/(Rbtbh2) от деформации крайнего сжатого волокна бетона еb при относительно больших коэффициентах армирования м (относительное продольное усилие отсутствует (вn=pn=0)).

Характер изменения относительной высоты зоны над трещиной и1 и относительной высоты сжатой зоны о в процессе увеличения деформации в крайнем сжатом волокне бетона еb представлен на рисунках 4 — 5. Он отражает известный из опытов и описанный в книге [3] феномен увеличения при определённых условиях высоты сжатой зоны в процессе увеличения нагрузки.

Достижение в крайнем волокне сжатого бетона предельного сопротивления сжатию, а в растянутой арматуре предела текучести означает переход рассматриваемого сечения в предельное состояние. Но реализация самого предельного состояния является не мгновенным актом, а процессом, связанным с развитием в арматуре деформаций по площадке текучести, в сжатом бетоне — с наполнением эпюры напряжений при уменьшающейся высоте сжатой зоны.

Далее сжатый бетон может достигнуть деформаций предельной сжимаемости, произойдёт раздробление сжатой зоны и разрушение сечения, либо растянутая арматура выйдет на ветвь упрочнения. Здесь возможно новое разветвление процесса: на участке упрочнения усилие в арматуре возрастает, соответственно должно возрастать и усилие в сжатом бетоне.

Это может быть достигнуто за счёт наполнения эпюры напряжений, если есть резерв для наполнения.

Если же резерв исчерпан и эпюра стала уже практически прямоугольной, то увеличение усилия в сжатой зоне может быть только в результате увеличения высоты сжатой зоны. Происходит частичное закрытие трещины в её вершине. Эти составные части процесса хорошо видны на рисунках 4 — 6.

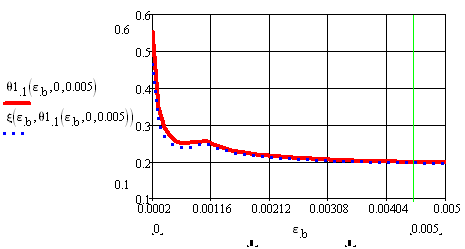
Рисунок 4 Зависимости относительной высоты зоны над трещиной и1=(h-hcrc)/h=1-и и относительной высоты сжатой зоны о от деформации крайнего сжатого волокна бетона еb при м =0,005(относительное продольное усилие отсутствует (вn=pn=0)).

При малом коэффициенте армирования (рисунок 4) имеется очень короткий отрезок деформаций еb, при которых сжатая часть сечения подрастает, дальше идёт длинный участок небольшого уменьшения высоты сжатой зоны вплоть до её разрушения.

При среднем коэффициенте армирования (рисунок 5) отрезок деформаций еb, при которых сжатая часть сечения подрастает, существенно больше.

И при относительно большом коэффициенте армирования (рисунок 6) начальный участок резкого уменьшения высоты сжатой зоны сменяется длинным пологим участком увеличения высоты сжатой зоны.

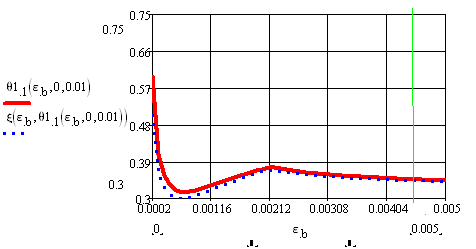
Рисунок 5 Зависимости относительной высоты зоны над трещиной и1=(h-hcrc)/h=1-и и относительной высоты сжатой зоны о от деформации крайнего сжатого волокна бетона еb при м =0,01(относительное продольное усилие отсутствует (вn=pn=0)).

Рисунок 6 Зависимости относительной высоты зоны над трещиной и1=(h-hcrc)/h=1-и и относительной высоты сжатой зоны о от деформации крайнего сжатого волокна бетона еb при м =0,02 (относительное продольное усилие отсутствует (вn=pn=0)).

На рисунках 7 — 11 показаны различные варианты реализации усилий в растянутой арматуре. Графики рисунков 7, 8 относятся к очень мало армированным элементам. Эти графики экстраполированы далеко за область физически возможных деформаций наиболее сжатого волокна бетона, чтобы показать, при каких максимальных деформациях в сжатой зоне возможен разрыв мягкой арматурной стали. Видно, что даже при запредельно малом коэффициенте армирования (м=0,0001, рисунок 7) в момент разрушения сжатой зоны бетона растянутая арматура находится на участке ветви упрочнения в пределах 40% её длины. При несколько большем, хотя и тоже малом, армировании (м=0,0005, рисунок 8) в момент разрушения сжатой зоны арматура оказывается на начальном участке ветви упрочнения, а при м=0,005 (рисунок 9) — в середине площадки текучести. В случае среднего коэффициента армирования м=0,01 (рисунок 10) разрушение сжатого бетона происходит в стадии деформирования растянутой арматуры на площадке текучести. При относительно высоком коэффициенте армирования (м=0,02, рисунок 11) деформации в арматуре в стадии разрушения сжатой зоны не достигают предела текучести. Следует отметить, что на линейном участке диаграммы деформирования стали (до предела текучести) при м=0,01 и, тем более, при м=0,02 зависимость усилия в арматуре от деформации в бетоне нелинейная вследствие нелинейности еb.

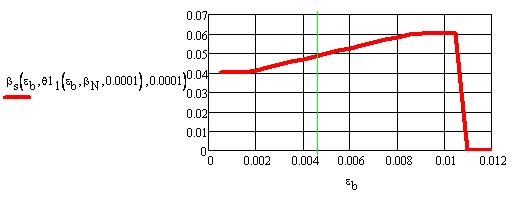
Рисунок 7 Зависимость относительного усилия в растянутой арматуре вs=ps от деформации в крайнем сжатом волокне бетона еb при м =0,0001 (относительное продольное усилие отсутствует (вn=pn=0); вертикальная линия между делениями 0,004 и 0,006 соответствует предельной сжимаемости бетона).

Рисунок 8 Зависимость относительного усилия в растянутой арматуре вs=ps от деформации в крайнем сжатом волокне бетона еb при м =0,0005 (относительное продольное усилие отсутствует (вn=pn=0); вертикальная линия между делениями 0,0025 и 0,005 соответствует предельной сжимаемости бетона)

Рисунок 9 Зависимость относительного усилия в растянутой арматуре вs=ps от деформации в крайнем сжатом волокне бетона еb при м =0,005 (относительное продольное усилие отсутствует (вn=pn=0); вертикальная линия между делениями 0,0 и 0,01 соответствует предельной сжимаемости бетона)

Рисунок 10 Зависимость относительного усилия в растянутой арматуре вs=ps от деформации в крайнем сжатом волокне бетона еb при м =0,01 (относительное продольное усилие отсутствует (вn=pn=0); вертикальная линия между делениями 0,004 и 0,005 соответствует предельной сжимаемости бетона)

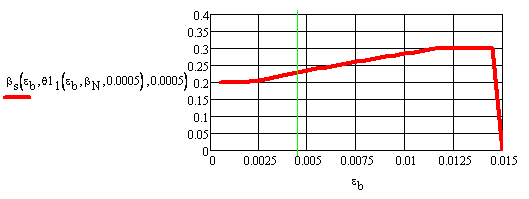
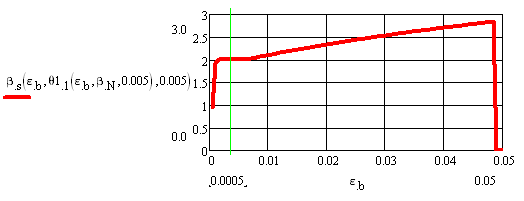
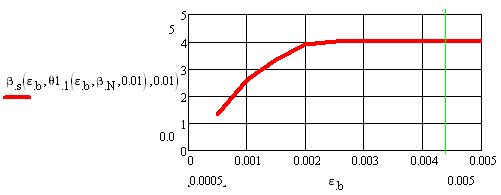
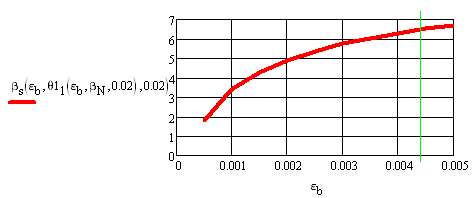
Рисунок 11 Зависимость относительного усилия в растянутой арматуре вs=ps от деформации в крайнем сжатом волокне бетона еb при м =0,02 (относительное продольное усилие отсутствует (вn=pn=0); вертикальная линия между делениями 0,004 и 0,005 соответствует предельной сжимаемости бетона).

Выводы

• 1. Составлены и решены уравнения, описывающие напряжённо-деформированное состояние нормальных сечений изгибаемых и внецентренно нагруженных железобетонных элементов на всех стадиях работы, от упругой до разрушения, с использованием нелинейных диаграмм деформирования бетона и арматуры.
• 2. Показаны особенности эксплуатационной стадии, в которой возрастание нагрузки может сопровождаться в зависимости от степени армирования сечения уменьшением или увеличением сжатой зоны.
• 3. Дифференциация стадии разрушения (например, выяснение уровня деформирования арматуры при отказе сжатой зоны бетона), не нужная при решении обычны задач проектирования, необходима при расчёте конструкций на особые воздействия, когда допускаются локальные разрушения (без разделения конструкции на части).

• 1. Маилян Д. Р., Кургин К. В. О необходимости трансформации базовой аналитической зависимости «уb-еb» бетона // Инженерный вестник Дона. 2011. № 4 URL: ivdon.ru/ru/magazine/archive/n4y2011/712.
• 2. Косенко Е. Е., Косенко В. В., Черпаков А. В. К вопросу о влиянии геометрических размеров на прочностные характеристики арматурных сталей // Инженерный вестник Дона. 2010. № 4 URL: ivdon.ru/ru/magazine/archive/n4y2010/318.
• 3. Пересыпкин Е. Н. Расчёт стержневых железобетонных элементов. М.: Стройиздат, 1988. 168 с.
• 4. Мурашев В. И. Трещиностойкость, жёсткость и прочность железобетона. М.: Машстройиздат, 1950. 268 с.
• 5. Сен-Венан Б. Мемуар о кручении призм. Мемуар об изгибе призм. М.: Физматгиз, 1961. 518 с.
• 6. Пересыпкин Е. Н., Шевцов С. В. Расчётные уравнения для нормальных сечений изгибаемых железобетонных элементов с учётом сопротивления бетона распространению трещин // Строительная механика и расчёт сооружений. 2010. № 3. С. 39−44.
• 7. Иваненко А. Н., Иваненко Н. А., Пересыпкин Е. Н., Пересыпкин С. Е. Напряженно-деформированное состояние стержневых железобетонных внецентренно нагруженных элементов в стадии трещинообразования // Инновации. Менеджмент. Маркетинг. Туризм: Мат-лы 2-й Междунар. науч.-практ. конф./Под науч. ред. А. М. Ветитнева, Н. С. Матющенко. Сочи: РИЦ ФГБОУ ВПО «СГУ», 2014. С. 162−165.
• 8. Гусаков В. Н. Исследование и разработка методов расчёта по деформациям и несущей способности изгибаемых и внецентренно сжатых железобетонных элементов конструкций из плотного силикатного бетона при статических нагружениях.: дис. … д-р. техн. наук: 05.23.01. М., 1978. 580 с.
• 9. E.N. Peresypkin, V.P. Pochinok, V.S. Shevtsov, S.V. Shevtsov. Impact of Concrete Type on Crack Resistance of Reinforced Concrete Constructions. European researcher / International Multidisciplinary Journal, 2012, N 5−2 (21), p. 622−625.
• 10. Nauss D.J. and Lott J.L. Fracture Toughness of Portland Cement Concretes/ - Journal of the American Concrete Institute. Vol. 66, No. 6, June, 1969, pp. 481−489.
• 11. Иваненко А. Н., Иваненко Н. А., Пересыпкин Е. Н. Трещиностойкость железобетонных конструкций как функция предельной растяжимости бетона // Инженерный вестник Дона. 2014. № 3 URL: ivdon.ru/ru/magazine/archive/n4y2010/318.