Основания квантовой механики – «теорфизическая» парадигма

Следуя объектному подходу (см. гл. 9), выделим «основания раздела науки» (ОРН) квантовой механики. Его составляют постулаты Шрёдингера^[1], Борна, «процедура квантования затравочной классической системы» Гейзенберга — Бора и «принцип тождественности» квантовых частиц для многочастичных систем. Они являются общепризнанными основаниями современной «новой» квантовой механики, и с их помощью наполняются конкретным содержанием обозначенные на схеме 9.2.1 функциональные места.

Под постулатами Шрёдингера здесь имеются в виду: 1) математический образ состояния квантовой системы в виде " волновой функции" ??(t) (ее часто называют ?-функцией)^[2] и 2) уравнение Шредингера в качестве уравнения движения, куда входит оператор Гамильтона Hкв, являющийся математическим образом квантово-механической системы (включая внешние условия).

То есть в случае квантовой механики на схеме 9.2.1 математическим образом SA (tj) является ??(tj), а уравнением движения является уравнение Шрёдингера (схема 15.3.1). В силу того, что уравнение Шрёдингера — это уравнение волнового типа, то его постулаты ответственны за волновые свойства движения квантовой частицы. При этом связь состояний здесь, как и в классической физике, абсолютно детерминистична. В постулаты Шрёдингера следует включить и принцип суперпозиции, утверждающий, что если есть два состояния, описываемые волновыми функциями ?1 и ?2, то существуют состояния, описываемые волновыми функциями («?, + b?2) с любыми коэффициентами а и b.

Постулаты Борна ответственны за появление в квантовой механике вероятности и за сочетание корпускулярных и волновых свойств. Это центральные постулаты квантовой механики. Нечеткость их формулировки — одна из причин существования множества «интерпретаций» квантовой механики. Предлагаемая здесь формулировка звучит так: 1) в квантовой механике состояние физической системы определяется не значениями, а распределениями вероятностей значений соответствующих измеримых величин^[3], т. е. состояние описывается случайными величинами^[4]; 2) из этого следует, что одно измерение ничего не говорит о состоянии системы (если оно не приготовлено в особом «собственном» состоянии)^[5], поскольку, чтобы определить распределение вероятностей, требуется длинная серия измерений^[6]; 3) задаются правила «вероятностной интерпретации волновой функции», позволяющие по математическому образу состояния ?A (t) определить распределения вероятностей соответствующих измеримых величин (для чего вводятся операторы измеримых величин или отвечающие им функции-орты^[7] (каковыми служат собственные функции этих операторов) в гильбертовом пространстве волновых функций)^[8].

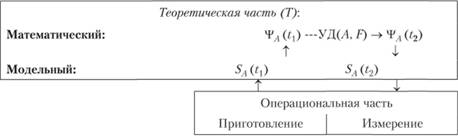
Схема 15.3.1. Структура оснований квантовой механики.

Постулаты Борна — это последовательный путь введения вероятности в квантовую механику^[9], причем вероятности как природного качества, а не результата незнания. Эти постулаты ничего не говорят о том, что будет с системой или ее состоянием после измерения.

Постулаты Шрёдингера и Борна определяют основные свойства квантовых систем: вероятностный тип поведения и корпускулярно-волновой дуализм^[10]. Сочетание корпускулярных и волновых свойств здесь хорошо иллюстрируется примером описанного выше двухщелевого эксперимента (см. схему 15.1.1). В соответствии с постулатами Борна каждое отдельное измерение дает локальную точку на втором экране-фотопластинке (корпускулярное свойство), но если провести много измерений, то проявится соответствующее распределение вероятностей, отвечающее дифракционноинтерференционной картине (волновые свойства) прохождения волны через две щели (при этом вопрос: «через какую щель проходит частица?» — на самом деле оказывается неадекватным: у микрочастицы, как и у волны, нет локализованной траектории^[11]).

Однако постулатов Шрёдингера и Борна недостаточно. Чтобы задать квантово-механическую систему, состоящую из одной или многих квантовых частиц, надо указать способ построения математического образа физической системы — квантового оператора Гамильтона Hкв, который входит в «уравнение движения». Стандартную процедуру его построения можно представить в виде процедуры квантования «затравочной классической системы» .

Эта процедура состоит в следующем. Исходной точкой здесь является классическая модель системы, например планетарная модель атома. Для нее строится классический математический образ (например, классический гамильтониан Н(х, р) в декартовой системе координат, являющийся функцией от положений (х) и импульсов (р) частиц). Затем проводится процедура квантования в виде замены этого классического математического образа соответствующим оператором (например, компоненту импульса частицы рх меняют на оператор 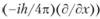. В результате получают квантовый гамильтониан Hкв^[12], т. е. математический образ квантовой системы, отвечающий квантово-механической физической модели. Так получается квантово-механическая модель атома с делокализованными состояниями («орбитами») электронов в атоме^[13]. В такой форме, но без такого особого названия этот метод был сформулирован в фундаментальных работах 1927−1930 гг. Джона фон Неймана и Поля Дирака [30; 14, с. 156].

По сути, он появляется уже в первых основополагающих работах В. Гейзенберга (1925), а у Луи де Бройля он существует под именем «автоматический вывод волнового уравнения» 112, с. 45]. В 1949 г. Бор излагает дело так: «Гейзенберг (1925) заложил основы рациональной квантовой механики, которая получила быстрое развитие благодаря важным вкладам Борна и Иордана, а также Дирака. Теория вводит формальный аппарат, в котором кинематические и динамические переменные классической механики заменяются абстрактными символами, подчиняющимися некоммутативной алгебре» [6, т. 2, с. 404−405]. Последние есть не что иное, как операторы (в современной терминологии). При этом, по утверждению Джеммера, «фундаментальной особенностью, характерной для подхода Гейзенберга, был способ использования принципа соответствия Бора… Гейзенберг… рассмотрел… возможность „угадать“ — в согласии с принципом соответствия — не решение частной квантово-механической задачи, а математическую схему новой механики» [13, с. 199]. Поэтому рассматриваемую «процедуру квантования затравочной классической системы» в «новой» квантовой теории можно считать гейзенберговским обобщением боровского «принципа соответствия» «старой» квантовой теории^[14].

В предлагаемой «теорфизической» формулировке указанная процедура «квантования» возводится в ранг теоретического постулата, входящего в базовую систему исходных понятий и постулатов квантовой механики (ее оснований (ОРН)), подобно тому, как Бор возводил в ранг «чисто теоретического закона» свой «принцип соответствия» в «старой» квантовой теории [6, т. 1, с. 505]. «Вследствие этого, — говорит Дирак о рассматриваемой процедуре, — мы можем в большинстве случаев употреблять для описания динамических систем в квантовой теории тот же язык, что и в классической теории (например, можем говорить о частицах с определенными массами, движущихся в заданном поле сил), и если нам дана система в классической механике, то обычно можно придать смысл понятию „той же самой“ системы в квантовой механике» [14, с. 156]. Так, затравочной классической моделью квантовой частицы является классическая механическая частица. Именно поэтому «первичным» идеальным объектом квантовой механики является «квантовая частица», обладающая и волновыми свойствами (а в квантовой теории поля — квантованная волна, обладающая и корпускулярными свойствами). Таким образом, благодаря процедуре квантования «затравочной классической системы» классическая физика оказалась встроенной в основания квантовой физики^[15]. В этом состоит объяснение вызывавшего иногда недоумение факта, что термины классической механики типа «положение», «скорость», «орбита» продолжали играть важную роль в изложении формализма, хотя все его развитие основывалось на отказе от таких понятий [13, с. 313−314].

Из места «затравочной классической модели» в базовой системе исходных понятий и постулатов квантовой механики вытекает то, что в нерелятивистской квантовой механике фигурируют те же измеримые величины, что и в классической физике (то же можно сказать и о «процедурах приготовления», которые тоже предполагают «затравочную классическую модель»^[16]). Именно из этого использования «затравочной классической модели» следует, что результаты наблюдения в нерелятивистской квантовой механике «выражаются с помощью классических понятий», но никакого боровского «должны выражаться» [6, т. 2, с. 57] здесь нет, могут появиться и неклассические измеримые величины, например «очарование» или «цвет», в релятивистской квантовой механике. Что касается «психологической сущности наблюдения и языка», к которой апеллировал Бор, то человеческий язык способен выражать не только наглядные понятия. Обсуждавшийся в гл. 9 гильбертовский неявный тип определения, на котором основывается теоретическая физика, как раз и позволяет это делать.

Итак, " квантовая частица"  — новый «первичный идеальный объект», определяемый базовой системой исходных понятий и постулатов квантовой механики (ее ОРН), созданной в 1925—1927 гг. Естественно, что свойства квантовой частицы существенно отличаются от свойств классической частицы.

Ярким ее отличием является «соотношение неопределенностей» Гейзенберга, которое утверждает, что для двух «взаимодополнительных» величин, относящихся к состоянию физической системы (например, компонент положения х и импульса рх), произведение их неопределенностей (квадратных корней дисперсий соответствующих функций распределения ?x и ?рх) отвечает условию ?х?рх ? h/4. «Взаимодополнительность» — новое для физики свойство, утверждающее, что измеримые величины, отвечающие состоянию «затравочной классической модели» системы, содержат пары взаимодополнительных величин. Математическим выражением этого свойства является некоммутативность (т.е. ab  bа) математических образов (так называемых операторов) измеримых величин, а физическим выражением свойства взаимодополнительности является само «соотношение неопределенностей», которое представляет собой не дополнительный постулат (принцип), а следствие постулатов Шрёдингера и Борна: оно теоретически выводится из них [13, с. 324−325]. Состояние, полностью описываемое волновой функцией, определяет распределение вероятностей для всех измеримых величин, включая взаимодополнительные.

Соответственно соотношение неопределенностей есть свойство состояния, а не измерения типа «меря одну величину, возмущаем другую», хотя часто можно встретить обратное утверждение. При этом в качестве иллюстрации последнего приводят известный мысленный эксперимент по измерению положения электрона с помощью гамма-микроскопа Гейзенберга: чем точнее хотим померить координату электрона, тем короче должна быть длина волны гамма-кванта, сталкивающегося с электроном, но тогда будет больше переданный электрону при их столкновении импульс. На самом деле здесь демонстрируется лишь соотношение неопределенности для состояния самого гамма-кванта, и ничего более (столкновение с электроном к этому ничего нс добавляет). Физическую суть соотношения неопределенностей выявляет другой мысленный эксперимент: состояние с заданным положением частицы можно приготовить с помощью экрана с маленькой щелью, но в силу дифракции после прохождения щели будет большая неопределенность по направлению импульса; расширяя щель, мы будем увеличивать неопределенность положения и уменьшать неопределенность по импульсу за счет уменьшения эффекта дифракции; состоянию частицы с определенным импульсом отвечает плоская волна, характеризующаяся полной нелокализованностыо в пространстве. Соотношение неопределенностей является следствием волновых свойств квантовых частиц (корпускулярно-волновых, но с акцентом на последнем). Измерение в квантовой механике, как и в других разделах физики (по определению, по своему функциональному месту на схеме 9.2.1), проявляет, а не создает существующее состояние (создавать — это прерогатива процедур приготовления, использующих фильтры и другие приборы).

Следует иметь в виду, что «соотношение неопределенностей» Гейзенберга, касающееся взаимодополнительных величин, характеризующих состояние системы, необходимо отличать от так называемого соотношения неопределенностей время-энергия, которое относится к описанию не состояния, а процесса. Здесь в рамках теории возмущений получают неравенство Гj?Ej > h/2?, вводя понятия квазистационарного состояния с энергией Е,•, неопределенности энергии этого состояния?? j (которую в случае атома называют «шириной уровня») и «времени жизни» Гj, системы в данном состоянии [21, т. 3]^[17]. Если заменить «время жизни» .

Гj на At, то получится выражение, по виду аналогичное «соотношению неопределенностей» Гейзенберга^[18], но оно совсем по-другому выводится (в рамках теории возмущений) и имеет другой смысл [21; 24].

В ОРН входит также описание процедур построения ВИО из ПИО. В квантовой механике модель физической системы, т. е. ВИО, строится, во-первых, путем конкретизации измеримых величин, характеризующих квантовую частицу и ее состояния. В результате этого квантовая частица превращается в электрон со спином или без спина, протон, фотон и т. д. Во-вторых, в квантовой механике, как и в классической, возможно построение многочастичных систем.

В последнем случае требуется добавить к перечисленным выше постулатам принцип тождественности (неразличимости) квантовых частиц, который определяет правила сборки многочастичных систем в квантовой механике. Из него следует «принцип Паули» для заполнения орбит электронов в атоме. Из него также следует наличие двух типов частиц — бозонов (фотоны) и фермионов (электроны, протоны, нейтроны), обладающих разными коллективными свойствами («статистиками»). Это холистский принцип, из-за которого система частиц не сводится к совокупности частиц. Без него нельзя описать явления сверхпроводимости и сверхтекучести при низких температурах, а также многие другие квантовые эффекты.

• [1] Можно исходить из постулатов Гейзенберга, которые эквивалентны постулатам Шрёдингера. Но в представлении (математическом представлении) Шрёдингера проще излагать физику дела, поэтому мы будем пользоваться им.
• [2] Поэтому у нее нет собственного физического смысла, поиском которого занимаются некоторые авторы, например [58].
• [3] Хотя это весьма распространенное среди физиков представление, оно редко четко формулируется в учебниках. Очень часто при изложении квантовой механики акцент делают на средних значениях, а не на распределении вероятностей, что сильно затрудняет понимание сути дела.
• [4] Понятия «случайность» и «вероятность» вводились разными авторами по-разному (см., например, работу [40]). Наиболее адекватной квантовой механике является, по-видимому, линия Мизеса — Колмогорова, где дается следующее определение вероятности Р(А) наступления события А: «Можно практически быть уверенным, что если комплекс условий 5 будет повторен большое число п раз и если при этом через т обозначить число случаев, при которых событие А наступило, то отношение т/п будет мало отличаться от Р(А)» [15, с. 5].
• [5] В силу этого копенгагенская интерпретация самопротиворечива, ибо, признавая вероятностное описание, нельзя связывать состояние с одним актом измерения.
• [6] При этом для выявления информации, ответственной за эффекты интерференции (содержащейся в фазе волновой функции), требуются томографические методы измерения состояний в квантовой механике, где для этого производят серии измерений взаимодополнительных величин [54, 56].
• [7] Так, в математическом слое вводятся математические образы измеримых величин, но не измерительных приборов, которые относятся к операциональной, а не к теоретической части.
• [8] По Л. де Бройлю, чья формулировка «вероятностной интерпретации волновой функции» Борна наиболее адекватна действиям современного физика-теоретика, она сводится к «принципу квантования» (не путать с «условиями (правилами) квантования» в «старой» квантовой теории) — «точное измерение какой-либо механической величины может дать в качестве значения этой величины лишь одно из собственных значений соответствующего оператора (измеримой величины. — А. Л.)» , — дополненному «принципом спектрального разложения», утверждающим, что «вероятности различных возможных значений некоторой механической величины, характеризующей частицу, полная Ψ-функция которой известна, пропорциональны квадратам (точнее, квадратам модуля. — А. Л) амплитуд соответствующих компонент спектрального разложения Ψ-функции по собственным функциям рассматриваемой величины» [11, с. 173−174].
• [9] Часто постулаты Борна сводят к третьему из перечисленных выше пунктов, но из него следует первый пункт, который является ключевым для понимания квантовой механики.
• [10] В «старой» квантовой теории акцент делался на дискретность характеристик (энергии, момента количества движения и др.) квантовых объектов (систем), но квантовая система в «новой» квантовой теории может обладать и непрерывными характеристиками. Здесь дискретность превращается в «корпускулярность» .
• [11] «Каждый фотон входит отчасти в каждую из двух компонент (интерферометра. — А. Л.). Тогда каждый фотон интерферирует лишь с самим собой. Интерференция между двумя разными фотонами никогда не происходит» , — заметил П. Дирак [14, с. 21].
• [12] Эта процедура с обсуждением некоторых опущенных здесь тонкостей приведена А. Мессиа как «общее правило построения уравнения Шрёдингера по принципу соответствия» [29, с. 75−78].
• [13] Эта процедура, которую мы назвали «квантованием затравочной классической модели», .может быть проведена с разной степенью полноты. Ею, в частности, определяется выбор квазиклассического (использующего сочетание «первичных идеальных объектов» квантовой механики и классической электродинамики) или последовательного квантовомеханического описания электромагнитного поля или фильтров (типа экрана с щелью).
• [14] «Принцип соответствия» Бора заключатся в «требовании непосредственного перехода квантово-теоретического описания в обычное в тех случаях, когда можно пренебречь квантом действия» [6, т. 2, с. 66], например для далеких атомных орбит. За счет этого определялись неизвестные параметры в формулах «старой» квантовой теории атома.
• [15] Квантовая механика как бы надстраивается над классической физикой, существенным образом используя ее физические модели, изменяя их. В более ранний, «классический» период метод «затравочной модели» не использовался. Новые разделы физики тогда создавай свои автономные модели.
• [16] Приготовление частиц с определенным импульсом, состояния которых описываются волновой функцией типа плоской волны, осуществляется с помощью нагретой спирали, их излучающей, и соответствующего фильтра.
• [17] Но, как и выше, этот вывод мы относим к взаимодействию объектов (подсистем) в ходе физического процесса, а не измерения. Кроме того, процесс измерения энергии, т. е. описание соответствующего эталона и процедур сравнения с ним, требует особого рассмотрения, ибо обычно значение энергии выражается через значения других величин, для которых эталон и процедуры сравнения с ним более очевидцы.
• [18] Здесь тоже можно подобрать волновую аналогию. Гармонической электромагнитной волне с частотой υ отвечает энергия фотона Λυ, но если электромагнитная волна конечна во времени и ее длительность характеризуется временем Т = At, то ей отвечает суперпозиция («пакет») гармонических волн разной частоты, приводящая к неопределенности в частоте Δυ = ½πΔt. Откуда после умножения на h следует At АЕ = h/2π.